Đề thi học sinh giỏi lớp 12 THPT tỉnh Thanh Hóa năm học 2010 - 2011 môn Toán (Có đáp án)

Vndoc.com xin gửi đến các bạn: Đề thi học sinh giỏi lớp 12 THPT tỉnh Thanh Hóa năm học 2010 - 2011 môn Toán (Có đáp án).

Đề thi học sinh giỏi môn Toán:

SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HÓA (Đề thi chính thức)

KỲTHI CHỌN HỌC SINH GIỎI LỚP 12 THPT CẤP TỈNH NĂM HỌC 2010- 2011 Ngày thi: 24/03/2011

MÔN THI: TOÁN
Thời gian làm bài: 180 phút (không kể thời gian giao đề)
--------------------------------------------------------------------------------

Câu I. (4,0 điểm).

Cho hàm số y = x³ - (m + 1)x² - (4 - m²⁾x - 1 - 2m (m là tham số thực), có đồ thị là (C_m)

1) Khảo sát sự biến thiên và vẽ đồ thị hàm số với m = − 1

2) Tìm các giá trị của m để đồ thị (C_m) có hai tiếp tuyến vuông góc với nhau.

Câu II. (6,0 điểm).

1) Giải phương trình: cos2x + cos3x - sinx - cos4x = sin6x.

2) Giải bất phương trình: (x thuộc R)

3) Tìm số thực a để phương trình: 9^x + 9 = a3^xcos(πx), chỉ có duy nhất một nghiệm thực.

Câu III. (2,0 điểm).

Tính tích phân: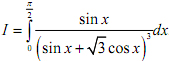

Câu IV. (6,0 điểm).

1) Cho tứ diện đều ABCD có độ dài cạnh bằng 1. Gọi M, N lần lượt là hai điểm thuộc các cạnh AB, AC sao cho mặt phẳng (DMN) vuông góc với mặt phẳng (ABC). Đặt AM = x, AN = y. Tìm x, y để diện tích toàn phần của tứ diện DAMN nhỏ nhất.

2) Trên mặt phẳng toạ độ Oxy cho đường thẳng Δ: x − y + 5 = 0 và hai elíp:
có cùng tiêu điểm. Biết rằng (E₂) đi qua điểm M thuộc đường thẳng Δ. Tìm toạ độ điểm M sao cho elíp (E₂) có độ dài trục lớn nhỏ nhất.

3) Trong không gian , Oxyz cho điểm M(0;2;0) và hai đường thẳng

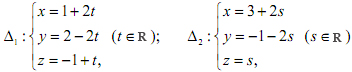
Viết phương trình mặt phẳng (P) đi qua M song song với trục Ox, sao cho (P) cắt hai đường thẳng Δ₁, Δ₂ lần lượt tại A, B thoả mãn AB = 1

Câu V. (2,0 điểm).

Cho các số thực a, b, c thoả mãn: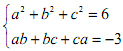

Tìm giá trịlớn nhất của biểu thức: P = a⁶ + b⁶ + c⁶