Đề thi học sinh giỏi tỉnh Nghệ An năm 2010 - 2011 môn Toán lớp 9 Bảng B (Có đáp án)
SỞ GIÁO DỤC VÀ ĐÀO TẠO
|
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 9 THCS
|
Câu 1 (5,0 điểm).
a) Chứng minh rằng với mọi số nguyên n thì n2 + n + 2 không chia hết cho 3.
b) Tìm tất cả các số tự nhiên n sao cho n2 + 17 là một số chính phương.
Câu 2 (5,0 điểm)
a) Giải phương trình: ![]()
b) Giải hệ phương trình: 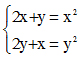
Câu 3 (3,0 điểm).
Tìm giá trị nhỏ nhất của biểu thức: ![]()
Câu 4 (4,5 điểm)
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Các đường cao BE, CF của tam giác ABC cắt nhau tại H.
a) Chứng minh rằng BH.BE + CH.CF = BC2
b) Gọi K là điểm đối xứng với H qua BC. Chứng minh rằng K thuộc (O).
Câu 5 (2,5 điểm).
Cho tam giác ABC nội tiếp đường tròn tâm O, một điểm I chuyển động trên cung BC không chứa điểm A (I không trùng với B và C). Đường thẳng vuông góc với IB tại I cắt đường thẳng AC tại E, đường thẳng vuông góc với IC tại I cắt đường thẳng AB tại F. Chứng minh rằng đường thẳng EF luôn đi qua một điểm cố định.



