Đề thi học sinh giỏi tỉnh Nghệ An năm 2010 - 2011 môn Toán lớp 9 Bảng A (Có đáp án)

SỞ GIÁO DỤC VÀ ĐÀO TẠO TỈNH NGHỆ AN (ĐỀ THI CHÍNH THỨC)

KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LỚP 9 THCS NĂM HỌC 2010 - 2011 MÔN THI: TOÁN - BẢNG A (Thời gian làm bài 150 phút không kể thời gian giao đề)

Câu 1 (4,0 điểm).

a) Cho các số nguyên a₁, a₂, a₃, ... , a_n. Đặt S = a₁³ + a₂³ + ... + a_n³ và P = a₁ + a₂ + ... + a_n.

Chứng minh rằng: S chia hết cho 6 khi và chỉ khi P chia hết cho 6.

b) Cho A = n⁶ - n⁴ + 2n³ + 2n² (với N thuộc N; n > 1). Chứng minh A không phải là số chính phương.

Câu 2 (4,5 điểm).

a) Giải phương trình:

b) Giải hệ phương trình: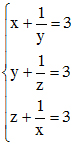

Câu 3 (4,5 điểm).

a) Cho x > 0, y > 0, z > 0 và .

Chứng minh rằng:

b) Cho x > 0, y > 0, z > 0 thỏa mãn x²⁰¹¹ + y²⁰¹¹ +z²⁰¹¹ = 3.

Tìm giá trị lớn nhất của biểu thức: M = x² + y² + z²

Câu 4 (4,5 điểm).

Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O), H là trực tâm của tam giác. Gọi M là một điểm trên cung BC không chứa điểm A. (M không trùng với B và C). Gọi N và P lần lượt là điểm đối xứng của M qua các đường thẳng AB và AC.

a) Chứng minh ba điểm N, H, P thẳng hàng.

b) Khi góc BOC = 120⁰, xác định vị trí của điểm M để đạt giá trị nhỏ nhất.

Câu 5 (2,5 điểm).

Cho tam giác ABC nội tiếp đường tròn tâm O, một điểm I chuyển động trên cung BC không chứa điểm A (I không trùng với B và C). Đường thẳng vuông góc với IB tại I cắt đường thẳng AC tại E, đường thẳng vuông góc với IC tại I cắt đường thẳng AB tại F. Chứng minh rằng đường thẳng EF luôn đi qua một điểm cố định.