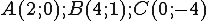Câu 1:
Trong mặt phẳng phức cho điểm A(2; -1). Điểm A' đối xứng với A qua đường phân giác của góc phần tư thứ nhất. Điểm A' biểu diễn số phức:- Đường phân giác của góc phần tư thứ nhất có phương trình là: y = x
- Gọi 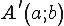 là điểm đối xứng của A qua đường thẳng d: y = x thì AA' vuông góc với d và trung điểm của AB thuộc d suy ra:
là điểm đối xứng của A qua đường thẳng d: y = x thì AA' vuông góc với d và trung điểm của AB thuộc d suy ra: 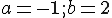
- Vậy A' biểu diễn của số số phức: z = -1 + 2i
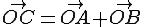 . C biểu diễn số phức:
. C biểu diễn số phức: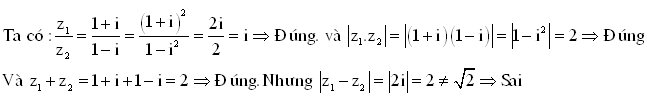
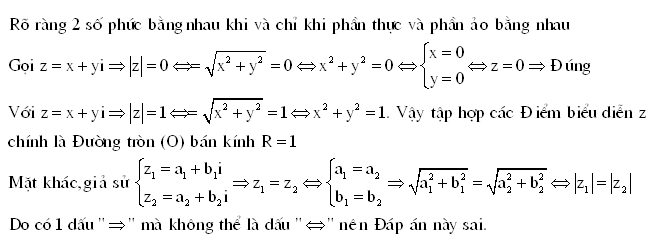
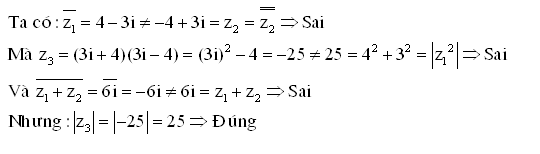
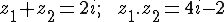
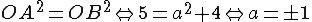
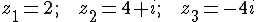 . M là điểm sao cho
. M là điểm sao cho 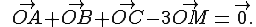 Khi đó M biểu diễn số phức:
Khi đó M biểu diễn số phức: