Đề thi cao học trường Đại học Ngoại Thương năm 2008 - Môn: Toán kinh tế

BỘ GIÁO DỤC VÀ ĐÀO TẠO TRƯỜNG ĐẠI HỌC NGOẠI THƯƠNG HỘI ĐỒNG TUYỂN SINH SAU ĐẠI HỌC NĂM 2008

ĐỀ THI TUYỂN SINH CAO HỌC ĐỢT II, NĂM 2008 MÔN THI: TOÁN KINH TẾ Thời gian làm bài: 180 phút (Không được phép dùng tài liệu)

Câu 1: Giải bài toán quy hoạch tuyến tính (N) sau đây: f(X) = x₁ + 5x₂ - x₃ + 2x₄ - 4x₅ - x₆ -> min

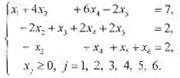
Câu 2: Xét bài toán quy hoạch tuyến tính (G) sau đây: f(X) = 4x₁ - 3x₂ - x₃ -> min

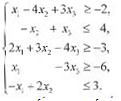
Các biến x có dấu tùy ý, j = 1, 2, 3

Viết bài toán đối ngẫu (G*) của (G). Chỉ ra các cặp ràng buộc đối ngẫu

Kiểm tra xem phương án X0 = (-1, 1, 1) có là phương án, phương án tối ưu của bài toán (G) không? Tại sao?

Câu 3: Có hai lô hàng đựng các sản phẩm. Lô thứ nhất có 10 sản phẩm tốt và 2 phế phẩm. Lô thứ hai cos 12 sản phẩm tốt và 3 phế phẩm. Từ lô thứ nhất lấy ngẫu nhiên 1 sản phẩm, từ lô thứ hai lấy ngẫu nhiên 2 sản phẩm.

Tìm xác suất có ít nhất 1 phế phẩm trong 3 sản phẩm lấy được

Gọi X là số phế phẩm trong 3 sản phẩm lấy ra từ hai lô hàng. Hãy lập bảng phân phối xác suất và tính kì vọng, phương án sai của X.

Câu 4: Tại một trại chăn nuôi gia cầm, cân thử một số con gà, người ta ghi được bảng số liệu sau đây:

Hãy ước lượng khối lượng trung bình của các con gà ở trại chăn nuôi đó với độ tin cậy 95%. Biết rằng khối lượng là đại lượng có phân phối chuẩn với giá trị của hàm số Laplace phi(1,96) = 0,475

Cho biết số liệu trên thu được sau khi trại chăn nuôi áp dụng chế độ chăm sóc mới đối với gia cầm. Còn trước đó tỉ lệ gà nặng trên 1,5kg là 25%. Hãy đánh giá hiệu quả của chế độ chăm sóc đó với mức ý nghĩa 1%, biết giá trị của hàm số Laplace phi(2,58) = 0,495

Lưu ý: Các kết quả ở câu 4 cần làm tròn đến 4 chữ số sau dấy phẩy