Đề minh họa thi HSG Toán 9 năm 2024 – 2025 sở GD&ĐT Bà Rịa – Vũng Tàu
Đề minh họa thi HSG Toán 9
Lớp:
Lớp 9
Môn:
Toán
Dạng tài liệu:
Đề thi HSG
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
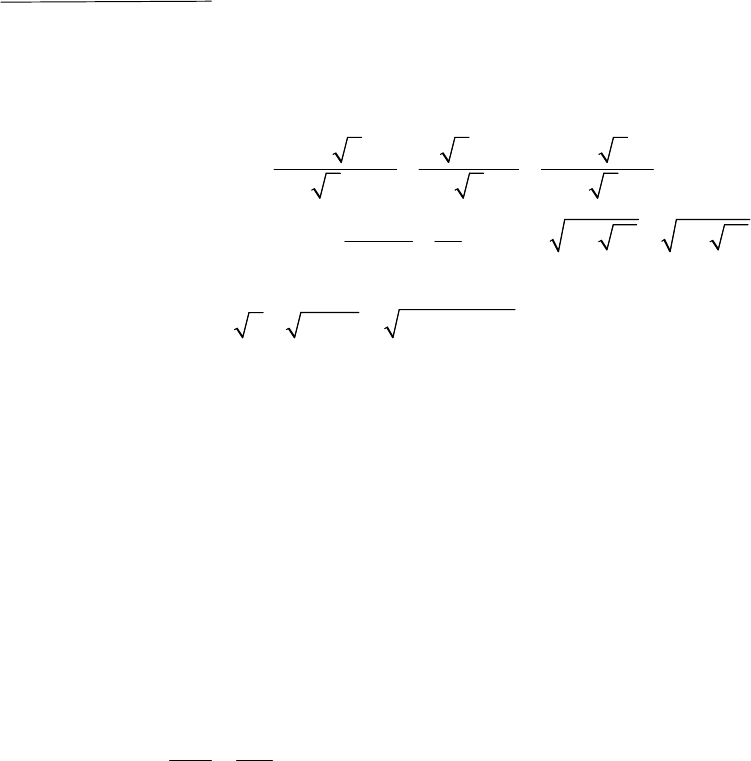
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH BÀ RỊA VŨNG TÀU
(ĐỀ MINH HỌA)
ĐỀ THI HỌC SINH GIỎI LỚP 9 CẤP TỈNH
NĂM HỌC 2024 – 2025
Môn thi : TOÁN
Thời gian làm bài : 150 phút
Đ
ề
minh h
ọ
a g
ồ
m có
01
trang
Bài 1 (3,0 điểm).
a) Rút gọn biểu thức :
3 2 4 1 3
8 2 2 4
x x x x
P
x x x x x x
với
0
x
và
1.
x
b) Tính giá trị của biểu thức :
4
14 20
3
x
A
x x
khi
3 3
5 17 5 17 .
x
Bài 2 (4,0 điểm).
a) Giải phương trình :
2
3 2 4 7 7.
x x x x
b) Tìm tất cả giá trị của tham số
m
để phương trình
2
1 3 0
x m x m
có hai nghiệm phân biệt
1 2
,
x x
thỏa mãn
2
1 2
.
x x
Bài 3 (4,0 điểm).
a) Tìm tất cả cặp hai số nguyên tố
;
p q
sao cho
2 2
4 3
p pq q
là một số chính phương.
b) Có hai cái hộp kín, hộp thứ nhất chứa sáu viên bi được đánh số từ
1
đến
6
và hộp thứ hai chứa mười
viên bi được đánh số từ
1
đến
10.
Các viên bi này có kích thước như nhau. Chọn ngẫu nhiên từ mỗi
hộp một viên bi. Tính xác suất chọn được hai viên bi mà tích hai số trên đó chia hết cho
6.
Bài 4 (5,0 điểm). Cho tam giác
ABC
có đường tròn
I
nội tiếp và tiếp xúc các cạnh , ,
BC CA AB
tương ứng
tại
, , .
D E F
Gọi
, ,
M N H
theo thứ tự là hình chiếu vuông góc của các điểm
, ,
B C D
trên đường thẳng
.
EF
a) Chứng minh
.
BM BD
CN CD
b) Chứng minh
HD
là phân giác của
.
BHC
c) Giả sử trên đoạn thẳng
EA
có điểm
P
và trên đoạn thẳng
FA
có điểm
Q
sao cho đường thẳng qua
,
P Q
tương ứng vuông góc với ,
AB AC
là hai tiếp tuyến của
I
và hai tiếp tuyến này cắt nhau tại
điểm
.
K
Chứng minh đường tròn tâm
K
và đi qua điểm
P
tiếp xúc với đường tròn đường kính
.
BC
Bài 5 (4,0 điểm).
a) Một mảnh giấy bìa cứng có dạng nửa hình tròn đường kính
4 .
AB dm
Người ta dự định cắt mảnh
giấy theo các cạnh , ,
AC CD DB
để tạo thành mảnh giấy hình thang cân
ACDB
có diện tích lớn
nhất (trong đó
,
C D
là hai điểm trên nửa đường tròn). Tìm giá trị lớn nhất đó.
b) Trên mặt phẳng cho
15
điểm sao cho không có ba điểm nào thẳng hàng. Người ta vẽ một số đoạn
thẳng nối hai trong số các điểm này sao cho không có ba cạnh của tam giác nào được vẽ. Chứng
minh số đoạn thẳng được vẽ không vượt quá
56.
-------------------HẾT-------------------
Họ và tên thí sinh : …………………………………………………….. ; Số báo danh : ……………………….
Chữ ký của CBCTh 01 : ……………………………………………….
Đề chọn học sinh giỏi Toán 9 năm 2024 – 2025 sở GD&ĐT Bà Rịa – Vũng Tàu được thiết kế bám sát chương trình, giúp học sinh phát triển tư duy và kỹ năng giải toán nâng cao.
Với nội dung được chọn lọc kỹ lưỡng, bài viết không chỉ giúp giáo viên hiểu rõ cấu trúc đề, ra đề sát với chuẩn năng lực mà còn là nguồn tài liệu hữu ích để nâng cao hiệu suất ôn thi cho học trò.



