Lý thuyết Vật lý 10 bài 4: Chuyển động thẳng CTST

Sách Chân trời sáng tạo

VnDoc xin giới thiệu bài Lý thuyết Vật lý lớp 10 bài 4: Chuyển động thẳng được chúng tôi sưu tầm và tổng hợp các câu hỏi lí thuyết và trắc nghiệm có đáp án đi kèm nằm trong chương trình giảng dạy môn Vật lý lớp 10 sách chân trời sáng tạo. Mời quý thầy cô cùng các bạn tham khảo tài liệu dưới đây.

A. Lý thuyết Vật lý 10 bài 4

1. Một số khái niệm cơ bản trong chuyển động

- Chất điểm: Một vật chuyển động được coi là chất điểm nếu kích thước của nó rất nhỏ so với quãng đường đi được hoặc so với khoảng cách mà ta đề cập đến.

Ví dụ: So với quãng đường đi từ Thành phố Hồ Chí Minh đến Thủ Đức Hà Nội (khoảng 1 730 km) thì một chiếc ô tô (có chiều dài trung bình khoảng 5 m) được xem là chất điểm.

- Vị trí: Để xác định vị trí của vật, ta cần chọn một vật khác làm gốc. Sau đó gắn vào vật này một trục Ox như Hình 1.1 (chuyển động thẳng) hoặc hệ tọa độ Oxy (chuyển động trong mặt phẳng). Khi đó, vị trí của vật có thể được xác định bởi toạ độ trên trục Ox hoặc (x, y) trong hệ trục Oxy.

Vị trí của một vật được xác định trên trục toạ độ tại hai thời điểm khác nhau

Hình 1.1. Vị trí của một vật được xác định trên trục toạ độ tại hai thời điểm khác nhau

Vật làm gốc, hệ trục tọa độ kết hợp với đồng hồ đo thời gian tạo thành hệ quy chiếu.

- Thời điểm: Thời gian có thể biểu diễn thành một trục gọi là trục thời gian. Chọn một điểm nhất định làm gốc thời gian thì mọi điểm khác trên trục thời gian được gọi là thời điểm.

- Quỹ đạo: Đường nối những vị trí liên tiếp của vật theo thời gian trong quá trình chuyển động.

2. Tốc độ

a. Tốc độ trung bình

- Đại lượng đặc trưng cho tính chất nhanh, chậm của chuyển động chính là tốc độ.

- Nếu trong khoảng thời gian vật di chuyển được một quãng đường thì:

Tốc độ trung bình của vật (kí hiệu v_tb) được xác định bằng thương số giữa quãng đường vật đi được và thời gian để vật thực hiện quãng đường đó.

$v_{tb}= \frac{{s}}{{\Delta t }}$ $v_{tb}= \frac{{s}}{{\Delta t }}$ (1.1)

- Trong hệ SI, đơn vị của tốc độ làm m/s (mét trên giây). Một số đơn vị thường dùng khác của tốc độ là km/h (kilômét trên giờ), km/s (kilômét trên giây),..

b. Tốc độ tức thời

- Để xét tính chất chuyển động nhanh, chậm của vật tại mỗi thời điểm, tốc độ phải được xét trong những khoảng thời gian rất nhỏ.

Tốc độ trung bình tính trong khoảng thời gian rất nhỏ là tốc độ tức thời (kí hiệu ) diễn tả sự nhanh, chậm của chuyển động tại thời điểm đó.

Khi một vật chuyển động với tốc độ tức thời không đổi, ta nói chuyển động của vật là chuyển động đều. Ngược lại, ta nói chuyển động của vật là không đều.

Trên thực tế, tốc độ tức thời được hiển thị bởi tốc kế trên nhiều phương tiện giao thông (Hình 1.2).

Tốc kế trên xe ô tô

Hình 1.2. Tốc kế trên xe ô tô

3. Vận tốc

a. Độ dịch chuyển

Xét hai tình huống chuyển động thẳng trên thực tế:

- Tình huống 1: Xét hai xe chuyển động ngược chiều nhau (Hình 1.3a). Chọn gốc tọa độ tại vị trí O, chiều dương hướng từ trái sang phải. Tại một thời điểm nào đó, xe màu xanh và xe màu cam đang lần lượt ở vị trí có tọa độ và. Sau khoảng thời gian, xe màu xanh đến được vị trí và xe màu cam đến được vị trí .

Khi đó:

Độ dịch chuyển của xe A: $d_A = x_B - x_A$

Độ dịch chuyển của xe B: ${d_A} = {x_B} - {x_A}$ ${d_A} = {x_B} - {x_A}$

- Tình huống 2: Xét một vận động viên bơi một vòng bế trong khoảng thời gian (Hình 1.3b). Chọn gốc tọa độ tại mép trái của bé bơi, chiều dương hướng từ trái sang phải và chiều dài bể bơi là

Khi đó: Độ dịch chuyển của vận động viên là l .

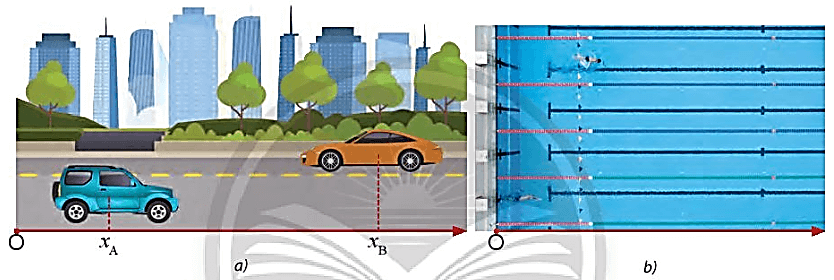
Một số trường hợp chuyển động thẳng trên thực tế

Hình 1.3. Một số trường hợp chuyển động thẳng trên thực tế

a) Hai xe chuyển động ngược chiều, b)Vận động viên đang bơi

Độ dịch chuyển được xác định bằng độ biến thiên tọa độ của vật.

$d = {x_2} - {x_1} = \Delta x$ $d = {x_2} - {x_1} = \Delta x$ (1.2)

Lưu ý:

- Tổng quát, độ dịch chuyển là một đại lượng vectơ $\overrightarrow d$ $\overrightarrow d$ có gốc tại vị trí ban đầu, hướng từ vị trí đầu đến vị trí cuối, độ lớn bằng khoảng cách giữa vị trí đầu và vị trí cuối.

- Độ dịch chuyển là một đại lượng có thể nhận giá trị dương, âm hoặc bằng không.Trong khi quãng đường đi được là một đại lượng không âm.

b. Vận tốc

Vận tốc trung bình là đại lượng vectơ được xác định bằng thương số giữa độ dịch chuyển của vật và thời gian để vật thực hiện độ dịch chuyển đó.

${\overline {\bf{v}} _{tb}} = \frac{{\overline {\bf{d}} }}{{\Delta t}} = \frac{{\Delta \overline {\bf{x}} }}{{\Delta t}}$ ${\overline {\bf{v}} _{tb}} = \frac{{\overline {\bf{d}} }}{{\Delta t}} = \frac{{\Delta \overline {\bf{x}} }}{{\Delta t}}$ (1.3)

Lưu ý: Tốc độ trung bình chỉ bằng độ lớn của vận tốc trung bình khi vật chuyển động thẳng không đổi chiều.

Xét trong một khoảng thời gian rất nhỏ, vận tốc trung bình sẽ trở thành vận tốc tức thời. Độ lớn của vận tốc tức thời chính là tốc độ tức thời.

Lưu ý: Như vậy, vận tốc tức thời cũng là một đại lượng vectơ $(\overrightarrow {\bf{v}})$ $(\overrightarrow {\bf{v}})$, có gốc tại vị trí vật chuyển động, hướng theo hướng của chuyển động và có độ dài tỉ lệ với độ lớn của vận tốc tức thời theo một tỉ xích xác định.

4. Đồ thị độ dịch chuyển – thời gian

a. Vẽ đồ thị dịch chuyển – thời gian dựa vào số liệu cho trước

Xét hai chuyển động với số liệu về tọa độ và thời điểm đi kèm: Chuyển động của con rùa theo đường thẳng (Hình 1.4) và chuyển động rơi của viên bị (Hình 1.5).

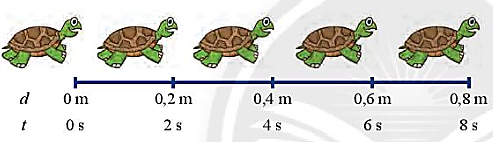
Số liệu về vị trí của con rùa sau những khoảng thời gian bằng nhau

Hình 1.4. Số liệu về vị trí của con rùa sau những khoảng thời gian bằng nhau

Mô phỏng viên bi rơi và bảng số liệu về vị trí của bi sau những khoảng thời gian bàng nhau

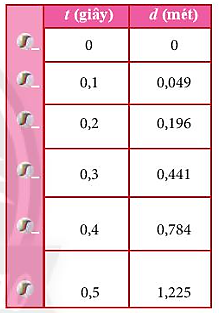
Hình 1.5. Mô phỏng viên bi rơi và bảng số liệu về vị trí của bi sau những khoảng thời gian bằng nhau

Chọn gốc tọa độ tại vị trí xuất phát, chiều dương (+) là chiều chuyển động. Đồ thị độ dịch chuyển - thời gian (d – t) như Hình 1.6.

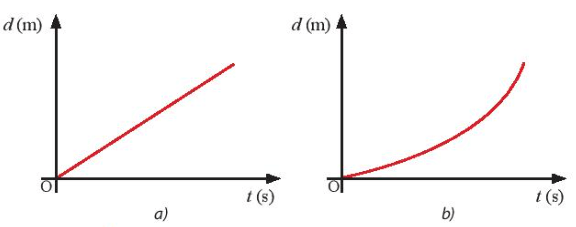
Phác thảo đồ thị (d – t) của hai chuyển động

Hình 1.6. Phác thảo đồ thị (d – t) của hai chuyển động

a) Chuyển động của con rùa; b) Chuyển động của viên bi

Từ các đồ thị (d – t), ta có nhận xét:

+ Đồ thị (d – t) mô tả chuyển động của con rùa là đường thẳng qua gốc toạ độ. Chuyển động của con rùa là chuyển động thẳng đều.

+ Đồ thị (d – t) mô tả chuyển động rơi của viên bị là đường cong qua gốc toạ độ. Độ dịch chuyển của viên bị trong những khoảng thời gian bằng nhau tăng lên nên chuyển động của viên bi là chuyển động thẳng nhanh dần.

Lưu ý: Các đồ thị (d – t) hay (x – t) là công cụ toán học thể hiện tính chất của chuyển động. Tránh nhầm lẫn với quỹ đạo của vật.

b. Xác định vận tốc từ độ dốc của đồ thị (d – t)

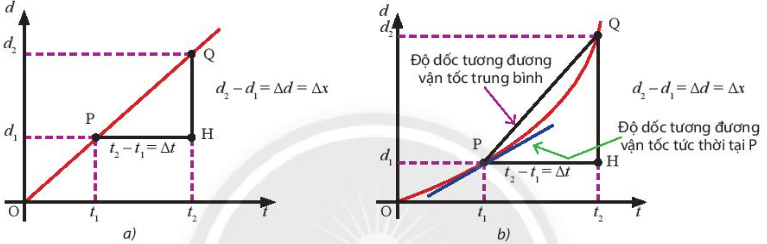
Minh họa cách xác định vận tốc tức thời từ đồ thị (d – t) của hai chuyển động

Hình 1.7. Minh họa cách xác định vận tốc tức thời từ đồ thị (d – t) của hai chuyển động:

a) Chuyển động của con rùa; b) Chuyển động rơi của viên bi

- Xét vật chuyển động từ vị trí 1 (tại thời điểm t₁) đến vị trí 2 (tại thời điểm t₂) lần lượt được biểu diễn bởi hai điểm P và Q trên đồ thị (d – t) trong Hình 1.7. So sánh với biểu thức (1.3) để xác định vận tốc trung bình, ta có: độ dịch chuyển của vật chính là đoạn , khoảng thời gian chính là độ dài PH.

- Từ đó, ta thấy vận tốc trung bình chính là độ dốc của đoạn PQ nối hai điểm trên đồ thị biểu diễn vị trí đầu đến vị trí cuối của vật.

Vận tốc tức thời của vật tại một thời điểm được xác định bởi độ dốc của tiếp tuyến với đồ thị (d – t) tại thời điểm đang xét.

Tốc độ tức thời tại một thời điểm chính là độ lớn của độ dốc tiếp tuyến của đồ thị (d – t) tại điểm đó.

B. Bài tập minh họa

Bài 1: Một vật chuyển động thẳng được mô tả như hình 1. Xác định tốc độ tức thời tại các vị trí A, B và C.

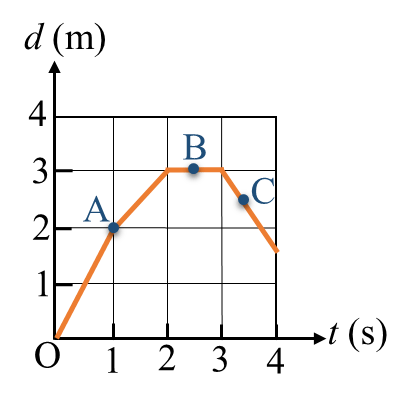
Hình 1. Đồ thị (d – t) của vật chuyển động

Hướng dẫn giải:

- Tốc độ tức thời tại vị trí A: ${v_A} = \frac{{{d_A}}}{{{t_A}}} = \frac{2}{1} = 2\,(m/s)\,$ ${v_A} = \frac{{{d_A}}}{{{t_A}}} = \frac{2}{1} = 2\,(m/s)\,$

- Tốc độ tức thời tại vị trí B: ${v_B} = \frac{{{d_B}}}{{{t_B}}} = \frac{{3,5}}{{2,5}} = 1,4\,(m/s)$ ${v_B} = \frac{{{d_B}}}{{{t_B}}} = \frac{{3,5}}{{2,5}} = 1,4\,(m/s)$

- Tốc độ tức thời tại vị trí C: ${v_C} = \frac{{{d_C}}}{{{t_C}}} = \frac{{2,5}}{{3,5}} \approx 0,71\,(m/s)$ ${v_C} = \frac{{{d_C}}}{{{t_C}}} = \frac{{2,5}}{{3,5}} \approx 0,71\,(m/s)$

Bài 2: Hai ô tô cùng khởi hành từ hai địa điểm A và B cách nhau 100 km, chuyển động cùng chiều, ô tô A có vận tốc 60 km/h, ô tô B có vận tốc 40 km/h. Chọn trục tọa độ là đường thẳng AB, gốc tọa độ tại A, chiều dương từ A đến B.

a) Lập công thức liên hệ giữa tọa độ và vận tốc của mỗi xe. Có mối liên hệ gì giữa các tọa độ khi hai xe gặp nhau?

b) Hai xe gặp nhau cách B bao nhiêu km?

Hướng dẫn giải:

a) Hệ thức liên hệ giữa tọa độ và vận tốc là: $x = {x_0} + v.t$ $x = {x_0} + v.t$

Với ${x_0}$ ${x_0}$là tọa độ ban đầu của vật so với gốc tọa độ; là tốc độ của vật.

Khi hai xe gặp nhau thì tọa độ của hai xe bằng nhau.

b) Biểu thức tọa độ của xe A là: ${x_A} = {x_{0A}} + {v_A}.t = 0 + 60.t\,(km)$ ${x_A} = {x_{0A}} + {v_A}.t = 0 + 60.t\,(km)$

Biểu thức tọa độ của xe B là: ${x_B} = {x_{0B}} + {v_B}.t = 100 + 40.t\,(km)$ ${x_B} = {x_{0B}} + {v_B}.t = 100 + 40.t\,(km)$

Khi hai xe gặp nhau:

$\begin{array}{l} {x_A} = {x_B} \Leftrightarrow 60.t = 100 + 40.t \Leftrightarrow t = 5\,(h)\\ \Rightarrow {x_A} = 300\,(km) \end{array}$ $\begin{array}{l} {x_A} = {x_B} \Leftrightarrow 60.t = 100 + 40.t \Leftrightarrow t = 5\,(h)\\ \Rightarrow {x_A} = 300\,(km) \end{array}$

Hai xe gặp nhau cách B là 200km