Chứng minh công thức liên hệ giữa gia tốc, vận tốc và quãng đường
Chuyển động thẳng biến đổi đều Vật lý 10
VnDoc xin giới thiệu tới bạn đọc tài liệu Chứng minh công thức liên hệ giữa gia tốc, vận tốc và quãng đường. Đây là tài liệu được biên soạn nhằm giúp quá trình ôn tập và củng cố kiến thức chuẩn bị cho kì thi học kì mới môn Vật lý của các bạn học sinh lớp 10 trở nên thuận lợi hơn. Mời các bạn tham khảo!
- Phương pháp giải bài tập Vật lý lớp 10 học kì 2 theo chủ đề
- Bài tập Vật lý lớp 10 - Tổng hợp và phân tích lực
- Bài tập vật lý lớp 10: Các nguyên lý nhiệt động lực học
- Bài tập Vật lý lớp 10 chương 7: Chất rắn, chất lỏng, sự chuyển thể
1. Gia tốc là gì?
- Đại lượng vật lý đặc trưng cho sự biến đổi nhanh chậm của vận tốc được gọi là gia tốc.
- Kí hiệu: a, đơn vị: 
\(m/s^2\)
- Gia tốc trung bình
+ Trong khoảng thời gian \(\Delta t={{t}_{2}}-{{t}_{1}}\), vecto vận tốc của chất điểm đã biến đổi một lượng \(\Delta \overrightarrow{v}=\overrightarrow{{{v}_{2}}}-\overrightarrow{{{v}_{1}}}\) ta có:
\(\frac{\Delta \overrightarrow{v}}{\Delta t}=\frac{\overrightarrow{{{v}_{2}}}-\overrightarrow{{{v}_{1}}}}{{{t}_{2}}-{{t}_{1}}}=\overrightarrow{{{a}_{tb}}}\)
Được gọi là vecto gia tốc trung bình của chất điểm
+ Vecto gia tốc trung bình có cùng phương, với quỹ đạo, giá trị đại số của nó là:
\({{a}_{tb}}=\frac{{{v}_{2}}-{{v}_{1}}}{{{t}_{2}}-{{t}_{1}}}=\frac{\Delta v}{\Delta t}\)
2. Chuyển động thẳng biến đổi đều
a. Định nghĩa: Chuyển động thẳng biến đổi đều là chuyển động thẳng trong đó gia tốc tức thời không đổi.
b. Sự biến đổi vận tốc theo thời gian
\(v-{{v}_{0}}=at\)
- Chọn chiều dương trên quỹ đạo, \(v,{{v}_{0}}\) lần lượt là vận tốc tại thời điểm t và thời điểm ban đầu \({{t}_{0}}=0\)
+ Nếu chuyển động là nhanh đàn đều thì \(a.v>0\)
+ Nếu chuyển động là chậm dần đều thì \(a.v<0\)
c. Phương trình chuyển động của chất điểm chuyển động thẳng biến đổi đều
\(x={{x}_{0}}+{{v}_{0}}t+\frac{1}{2}a{{t}^{2}}\) (1)
3. Công thức liên hệ giữa gia tốc, vận tốc và quãng đường
- Ta sẽ chứng minh mối liên hệ của gia tốc, vận tốc và quãng đường
Chứng minh:
Kí hiệu \(s=x-{{x}_{0}}\) là độ dời trong khoảng thời gian từ 0 đến t
Ta có: \(v-{{v}_{0}}=at\Rightarrow t=\frac{v-{{v}_{0}}}{a}(*)\)
Thay (*) vào (1) ta có:
\(\begin{align}
& x={{x}_{0}}+{{v}_{0}}t+\frac{1}{2}a{{t}^{2}} \\
& \Leftrightarrow x-{{x}_{0}}={{v}_{0}}.t+\frac{1}{2}a.{{t}^{2}} \\
& \Leftrightarrow s={{v}_{0}}.\frac{v-{{v}_{0}}}{a}+\frac{1}{2}.a.{{\left( \frac{v-{{v}_{0}}}{a} \right)}^{2}} \\
& \Leftrightarrow 2as=2{{v}_{o}}\left( v-{{v}_{0}} \right)+{{\left( v-{{v}_{0}} \right)}^{2}} \\
& \Leftrightarrow 2as=2.v.{{v}_{0}}-2.{{v}_{0}}^{2}+{{v}^{2}}-2.v.{{v}_{0}}+{{v}_{0}}^{2} \\
& \Leftrightarrow 2as={{v}^{2}}-{{v}_{0}}^{2} \\
& \Rightarrow {{v}^{2}}-{{v}_{0}}^{2}=2as \\
\end{align}\)
4. Bài tập chuyên động thẳng biến đổi đều
Bài 1: Một chất điểm đang chuyển động thẳng đều với vận tốc 4m/s thì tăng tốc chuyển động nhanh dần đều.
a. Tính gia tốc của chất điểm biết rằng sau khi đi được quãng đường 8m thì nó đạt vận tốc 8m/s.
b. Viết phương trình chuyển động của chất điểm. Chọn chiều dương là chiều chuyển động, gốc tọa đọ trùng với vị trí chất điểm bắt đầu tăng tốc, gốc thời gian là lúc tăng tốc.
c. Xác định vị trí mà tại đó chất điểm có vận tốc 13m/s.
Hướng dẫn giải
a) Từ công thức \(v^{2} - v_{0}^{2} = 2as
\Rightarrow\) gia tốc: \(a =
\frac{v^{2} - v_{0}^{2}}{2s}\)
Thay số ta được: \(a = \frac{8^{2} -
4^{2}}{2.8} = 3\)m/s2.
b) Phương trình chuyển động có dạng: \(x =
v_{0}t + \frac{1}{2}at^{2}\).
Thay số ta được: \(x = 4t +
1,5t^{2}\)(m).
c) Ta có: \(v = v_{0} + at \Rightarrow t =
\frac{v - v_{0}}{a} = \frac{13 - 4}{3} = 3\)s.
Tọa độ của chất điểm lúc đó: \(x = 4.3 +
1,5.3^{2} = 25,5\)m.
Bài 2: Một đoàn tàu đang chạy với vận tốc 43,2km/h thì hãm phanh, chuyển động thẳng chậm dần đều đề vào ga. Sau 2,5 phút thì tàu dừng lại ở sân ga.
a. Tính gia tốc của đoàn tàu.
b. Tính quãng đường mà tàu đi được trong thời gian hãm.
Hướng dẫn giải
Chọn chiều dương là chiều chuyển động.
a) Gia tốc: \(a = \frac{v - v_{0}}{\Delta
t} = \frac{0 - 12}{2,5.60} = - 0,08\)m/s2.
b) Từ \(v^{2} - v_{0}^{2} = 2as
\Rightarrow\) quãng đường tàu đi được trong thời gian hãm:
\(s = \frac{v^{2} - v_{0}^{2}}{2a} =
\frac{0 - 12^{2}}{2.( - 0,08)} = 900\)(m).
Bài 3: Một vật bắt đầu chuyển động thẳng nhanh dần đều với vận tốc ban đầu 6m/s và gia tốc 4m/s2.
a. Vẽ đồ thị vận tốc theo thời gian của vật.
b. Sau bao lâu vật đạt vận tốc 18m/s. Tính quãng đường vật đi được trong khoảng thời gian đó.
c. Viết phương trình chuyển động của vật, từ đó xác định vị trí mà tại đó vận tốc của vật là 12m/s.
Hướng dẫn giải
Chọn chiều dương là chiều chuyển động, gốc tọa độ trùng với vị trí ban đầu của vật, gốc thời gian là xuất phát.
a) Phương trình vận tốc: \(v = 6 +
4t\)(m/s).
Đồ thị vận tốc - thời gian được biểu diễn như hình vẽ:
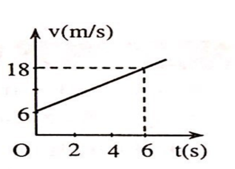
Khi \(v = 18\)m/s thì \(t = \frac{18 - 6}{4} = 3\)s.
Từ công thức \(v^{2} - v_{0}^{2} =
2as\)
\(\Rightarrow\) quãng đường \(s = \frac{v^{2} - v_{0}^{2}}{2a} = \frac{18^{2} -
6^{2}}{2.4} = 36\)m.
b) Phương trình chuyển động: \(x = 6t +
2t^{2}\) (m).
Khi \(v = 12\)m/s thì \(t = \frac{12 - 6}{4} = 1,5s \Rightarrow\) tọa độ \(x = 6.1,5 + 2.1,5^{2} =
13,5\)m.
----------------------------------------------------------
Trên đây VnDoc đã giới thiệu tới các bạn bài Chứng minh công thức liên hệ giữa gia tốc, vận tốc và quãng đường. Hy vọng với tài liệu này các bạn học sinh sẽ nắm chắc kiến thức vận dụng tốt vào giải bài tập từ đó học tốt môn Lý 10. Chúc các bạn học tốt và nhớ thường xuyên tương tác để cập nhật được nhiều bài tập hay bổ ích nhé!
