Bài tập Vật lý lớp 10 - Tổng hợp và phân tích lực
Bài tập Vật lý lớp 10 - Tổng hợp và phân tích lực
Bài tập Vật lý lớp 10 - Tổng hợp và phân tích lực là tài liệu hữu ích dành cho các bạn học sinh lớp 10 trong việc ôn tập và củng cố các kiến thức đã học môn Vật lý. Tài liệu này giúp các bạn học sinh hệ thống lại các vấn đề lý thuyết về lực, tổng hợp và phân tích lực. Các bài tập có đáp án đi kèm sẽ giúp các bạn ôn tập hiệu quả hơn. Mời các bạn tải về để tham khảo.
A. Kiến thức cần nhớ về Tổng hợp và phân tích lực
1. Đặc điểm của vectơ lực?
- Điểm đặt tại vật
- Phương của lực tác dụng
- Chiều của lực tác dụng
- Độ lớn tỉ lệ với độ lớn cả lực tác dụng
2. Cân bằng lực
- Các lực cân bằng là các lực cùng tác dụng vào một vật và không gây ra gia tốc cho vật.
- Hai lực cân bằng: là hai lực cùng tác dụng vào một vật, cùng giá, cùng độ lớn nhưng ngược chiều.
3. Tổng hợp lực là gì?
Tổng hợp là thay thế hai hay nhiều lực tác dụng đồng thời vào một vật bởi một lực sao cho tác dụng vẫn không thay đổi.
+ Lực thay thế được gọi là hợp lực.
+ Phương pháp tìm hợp lực được gọi là tổng hợp lực.
B. Cách tổng hợp lực, phân tích lực
1. Cách tìm hợp lực của hai lực bằng hình học
Bước 1. Tịnh tiến các lực về cùng điểm đặt.
Bước 2. Nếu các lực không cùng phương thì sử dụng quy tắc hình bình hành để xác định véc tơ tổng trên hình vẽ.
Bước 3. Sử dụng các công thức sau để tìm độ lớn của hợp lực.
\(F^2=F^2_1+F_2^2+2F_1F_2 \cos{\alpha}\) với \(\alpha=\left ( \vec{F_1},\vec{F_2} \right )\)
\(\dfrac{F}{\sin{\alpha_1}}=\dfrac{F}{\sin{\alpha_2}}=\dfrac{F}{\sin{\alpha_3}}\)
với α1, α2, α3 là các góc đối diện với các lực tương ứng (định lí hàm số sin).
Các trường hợp đặc biệt
- Nếu \(F_1=F_2=A\) thì \(F=A\sqrt{2+2\cos{\alpha}}=2A.\cos{\dfrac{\alpha}{2}}\)
- Nếu \(\vec{F_1}\perp \vec{F_2}\) thì \(F=\sqrt{F_1^2+F_2^2}\)
- Nếu \(\vec{F_1}\uparrow \uparrow \vec{F_2}\) thì \(F=F_1+F_2\)
- Nếu \(\vec{F_1}\uparrow \downarrow \vec{F_2}\) thì \(F=\left | F_1-F_2 \right |\)
Lưu ý: Nếu có hai lực, thì hợp lực có giá trị trong khoảng: |F2 - F1| ≤ Fhl ≤ |F1 + F2|
2. Cách tìm hợp lực của ba lực trở lên bằng phương pháp đại số
Bước 1. Chọn hệ trục tọa độ.
Bước 2. Xác định các góc \(\left ( \vec{F_1},Ox \right ) =\alpha_1;\left ( \vec{F_2},Ox \right )=\alpha_2; \left ( \vec{F_3},Ox \right ) =\alpha_3,...\)
Bước 3. Tìm hình chiếu của các lực trên trục:
\(\left\{\begin{matrix} F_x =F_1\cos{\alpha_1}+F_2\cos{\alpha_2}+F_3\cos{\alpha_3}+... \\ F_y =F_1\sin{\alpha_1}+F_2\sin{\alpha_2}+F_3\sin{\alpha_3}+... \end{matrix}\right.\)
Bước 4. Xác định độ lớn của hợp lực bởi công thức và bởi công thức \(F=\sqrt{F_x^2+F_y^2}\)
\(\left ( \vec{F},Ox \right )=\alpha\) bởi công thức \(\left [ \begin{matrix}\tan{\alpha}=\dfrac{F_x}{F_y}\Leftrightarrow F_x.F_y>0 \\\tan{\alpha}=-\dfrac{F_x}{F_y}\Leftrightarrow F_x.F_y<0\end{matrix} \right.\)
C. Bài tập tổng hợp lực, phân tích lực có đáp án
Bài 1. Cho hai lực đồng qui có cùng độ lớn 10 (N). Khi đó, hợp lực và góc hợp giữa hai lực thành phần có giá trị lần lượt là bao nhiêu?
ĐS. Fhl = 15 (N); α = 900.
Bài 2. Cho hai lực đồng qui có độ lớn F1 = F2 = 20 (N). Độ lớn của hợp lực là F = 34,6 (N) khi hai lực thành phần hợp với nhau một góc là bao nhiêu?
ĐS. 600
Bài 3. Cho hai lực đồng qui có độ lớn F1 = 16 (N), F2 = 12 (N). Độ lớn hợp lực của chúng có thể là bao nhiêu?
ĐS. F = 20 (N)
Bài 4. Cho hai lực đồng qui có cùng độ lớn 30 (N). Hỏi góc giữa hai lực bằng bao nhiêu thì hợp lực cũng có độ lớn bằng 30 (N)?
ĐS. 1200
Bài 5: Cho ba lực đồng qui cùng nằm trên một mặt phẳng, có độ lớn F1 = F2 = F3 = 20 (N) và từng đôi một với nhau hợp thành góc 1200. Hợp lực của chúng có độ lớn là bao nhiêu?
ĐS. F = 20 (N)
Bài 6. Một vật m = 5kg được giữ yên trên mặt phẳng nghiêng góc \(75^0\) so với phương ngang bằng một sợi dây mảnh và nhẹ, bỏ qua ma sát. Tìm lực căng của sợi dây (lực mà tác dụng lên sợi dây bị căng ra)?
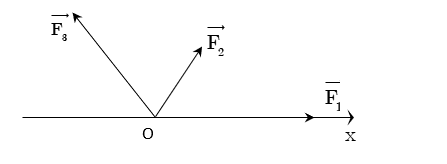
Bài 7. Cho ba lực đồng qui (tại điểm O), đồng phẳng \(\overrightarrow{F_{1}},\ \overrightarrow{F_{2}},\
\overrightarrow{F_{3}}\) lần lượt hợp với trục Ox những góc \(0^{o},\ 60^{o},\ 120^{o}\) và có độ lớn tương ứng là \(F_{1} = F_{3} = 2F_{2} =
10(N)\) như trên hình vẽ 1. Tìm hợp lực của ba lực trên?
ĐS: \(15(N)\).
Bài 8. Biết \(\overrightarrow{F} =
\overrightarrow{F_{1}} + \overrightarrow{F_{2}}\) và \(F_{1} = F_{2} = 5\sqrt{3}(N)\) và góc giữa \(\overrightarrow{F}\) và \(\overrightarrow{F_{1}}\) bằng \(30^{o}\). Độ lớn của hợp lực \(\overrightarrow{F}\) và góc giữa \(\overrightarrow{F_{1}}\) với \(\overrightarrow{F_{2}}\) bằng bao nhiêu?
ĐS: \(15(N)\) và \(60^{o}\)
Bài 9. Cho hai lực đồng quy có độ lớn \(4(N)\) và \(5(N)\) hợp với nhau một góc α. Tính góc α? Biết rằng hợp lực của hai lực trên có độ lớn bằng \(7,8(N)\).
ĐS: \(60^{o}15'\).
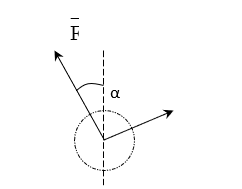
Bài 10. Một vật có khối lượng m chịu tác dụng của hai lực lực \(\overrightarrow{F_{1}}\) và \(\overrightarrow{F_{2}}\) như hình vẽ 4. Cho biết \(F_{1} = 34,64(N);\ F_{2} = 20(N);\
\alpha = 30^{o}\) là góc hợp bởi \(\overrightarrow{F_{1}}\) với phương thẳng đứng. Tìm m để vật cân bằng?
ĐS: \(m = 2(kg)\) hoặc \(m = 4(kg)\).
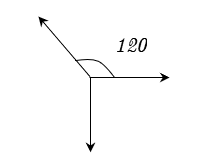
Bài 11. Một vật chịu tác dụng của ba lực như hình vẽ thì cân bằng. Biết rằng độ lớn của lực \(F_{3} =
40(N)\). Hãy tính độ lớn của lực F1 và F2?
ĐS: \(F_{1} = 23(N);\ \ F_{2} =
46(N)\)
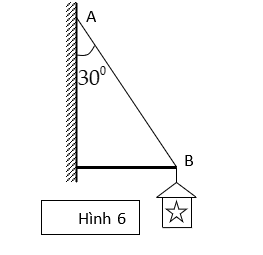
Bài 12. Một chiếc đèn được treo vào tường nhờ một dây AB. Muốn cho đèn ở xa tường, người ta dùng một thanh chống nằm ngang, một đầu tì vào tường, còn đầu kia tì vào điểm B của dây như hình vẽ 6. Cho biết đèn nặng \(4(kg)\) và dây hợp với tường một góc \(30^{o}\). Tính lực căng của dây và phản lực của thanh. Cho biết phản lực của thanh có phương dọc theo thanh và lấy \(g = 10\left( m/s^{2}
\right)\).
ĐS: \(15(N);\ 10(N)\).
(còn tiếp)
Mời bạn đọc tải tài liệu tham khảo để xem đầy đủ tài liệu!
