VnDoc.com

Cách tính góc giữa hai vectơ Toán 10

Góc giữa 2 vectơ Có đáp án

Bài trước

Tải về

Bài sau

Phân loại: Tài liệu Tính phí

Tính góc giữa hai vectơ trong Toán 10

A. Công thức góc giữa hai vectơ
- a. Công thức tính góc giữa hai vectơ
- b. Tích vô hướng của hai vectơ
B. Bài tập ví dụ minh họa tính góc giữa hai vectơ

Trong Toán học lớp 10, cách tính góc giữa hai vectơ là một trong những kiến thức quan trọng, giúp học sinh hiểu rõ hơn về mối quan hệ giữa các vectơ trong không gian. Việc tính toán góc giữa hai vectơ không chỉ có ứng dụng trong các bài toán hình học mà còn trong các lĩnh vực khoa học, kỹ thuật và động học. Trong bài viết này, chúng ta sẽ cùng nhau khám phá cách tính góc giữa hai vectơ, đồng thời giải quyết các bài toán có đáp án để bạn nắm vững phương pháp và kỹ thuật áp dụng một cách chính xác.

A. Công thức góc giữa hai vectơ

a. Công thức tính góc giữa hai vectơ

Trong không gian, cho hai vectơ $\overrightarrow{a}$ $\overrightarrow{a}$ và $\overrightarrow{b}$ $\overrightarrow{b}$ đều khác vectơ $\overrightarrow{0}.$ $\overrightarrow{0}.$ Từ một điểm $O$ bất kì ta vẽ $\overrightarrow{OA} = \overrightarrow{a}$ $\overrightarrow{OA} = \overrightarrow{a}$ và $\overrightarrow{OB} = \overrightarrow{b}$ $\overrightarrow{OB} = \overrightarrow{b}$.

Góc cho hai vectơ $\overrightarrow{a}$ $\overrightarrow{a}$ và $\overrightarrow{b}$ $\overrightarrow{b}$ trong không gian, kí hiệu $\left( \overrightarrow{a},\overrightarrow{b} \right)$ $\left( \overrightarrow{a},\overrightarrow{b} \right)$, là góc giữa hai vectơ $\overrightarrow{OA},\overrightarrow{OB}$ $\overrightarrow{OA},\overrightarrow{OB}$.

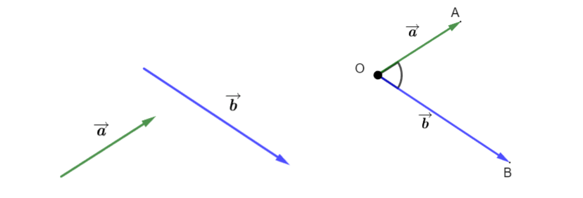
Chú ý:

$0^{o} \leq \left( \overrightarrow{a},\overrightarrow{b} \right) \leq 180^{o}$ $0^{o} \leq \left( \overrightarrow{a},\overrightarrow{b} \right) \leq 180^{o}$
Nếu $\left( \overrightarrow{a},\overrightarrow{b} \right) = 90^{0}$ $\left( \overrightarrow{a},\overrightarrow{b} \right) = 90^{0}$ thì ta nói rằng $\overrightarrow{a}$ $\overrightarrow{a}$ và $\overrightarrow{b}$ $\overrightarrow{b}$ vuông góc với nhau, kí hiệu là $\overrightarrow{a}\bot\overrightarrow{b}$ $\overrightarrow{a}\bot\overrightarrow{b}$.
Góc giữa hai vectơ cùng hướng và khác $\overrightarrow{0}$ $\overrightarrow{0}$ luôn bằng $0^{o}$ $0^{o}$.
Góc giữa hai vectơ ngược hướng và khác $\overrightarrow{0}$ $\overrightarrow{0}$ luôn bằng $180^{o}$ $180^{o}$.

b. Tích vô hướng của hai vectơ

Trong không gian, cho hai vectơ $\overrightarrow{a}$ $\overrightarrow{a}$ và $\overrightarrow{b}$ $\overrightarrow{b}$ đều khác vectơ $\overrightarrow{0}.$ $\overrightarrow{0}.$ Tích vô hướng của hai vectơ $\overrightarrow{a}$ $\overrightarrow{a}$ và $\overrightarrow{b}$ $\overrightarrow{b}$ là một số thực, kí hiệu $\overrightarrow{a}.\overrightarrow{b}$ $\overrightarrow{a}.\overrightarrow{b}$, được xác định bởi công thức sau:

$\overrightarrow{a}.\overrightarrow{b} = \left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|\cos\left( \overrightarrow{a},\overrightarrow{b} \right)$ $\overrightarrow{a}.\overrightarrow{b} = \left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|\cos\left( \overrightarrow{a},\overrightarrow{b} \right)$

B. Bài tập ví dụ minh họa tính góc giữa hai vectơ

Bài tập 1: Cho tam giác đều $ABC$. Tính $P = \cos(\overrightarrow{AB},\overrightarrow{BC}) + \cos(\overrightarrow{BC},\overrightarrow{CA}) + \cos(\overrightarrow{CA},\overrightarrow{AB}).$ $P = \cos(\overrightarrow{AB},\overrightarrow{BC}) + \cos(\overrightarrow{BC},\overrightarrow{CA}) + \cos(\overrightarrow{CA},\overrightarrow{AB}).$

A. $P = \frac{3}{2}$ $P = \frac{3}{2}$. B. $P = \frac{3\sqrt{3}}{2}$ $P = \frac{3\sqrt{3}}{2}$. C. $P = - \frac{3}{2}$ $P = - \frac{3}{2}$. D. $P = - \frac{3\sqrt{3}}{2}$ $P = - \frac{3\sqrt{3}}{2}$.

Hướng dẫn giải

Hình vẽ minh họa

Có $(\overrightarrow{AB},\overrightarrow{BC}) = (\overrightarrow{BB$ $(\overrightarrow{AB},\overrightarrow{BC}) = (\overrightarrow{BB'},\overrightarrow{BC}) = \widehat{B'BC} = 120{^\circ}$.

Có $(\overrightarrow{BC},\overrightarrow{CA}) = (\overrightarrow{CC$ $(\overrightarrow{BC},\overrightarrow{CA}) = (\overrightarrow{CC'},\overrightarrow{CA}) = \widehat{C'CA} = 120{^\circ}$.

Có $(\overrightarrow{CA},\overrightarrow{AB}) = (\overrightarrow{AA$ $(\overrightarrow{CA},\overrightarrow{AB}) = (\overrightarrow{AA'},\overrightarrow{AB}) = \widehat{A'AB} = 120{^\circ}$.

Suy ra $P = 3.cos120{^\circ} = - \frac{3}{2}$ $P = 3.cos120{^\circ} = - \frac{3}{2}$.

Bài tập 2: Tam giác $ABC$ vuông ở $A$ và có $BC = 2AC$. Tính $cos(\overrightarrow{AC},\overrightarrow{CB}).$ $cos(\overrightarrow{AC},\overrightarrow{CB}).$

Hướng dẫn giải

Hình vẽ minh họa

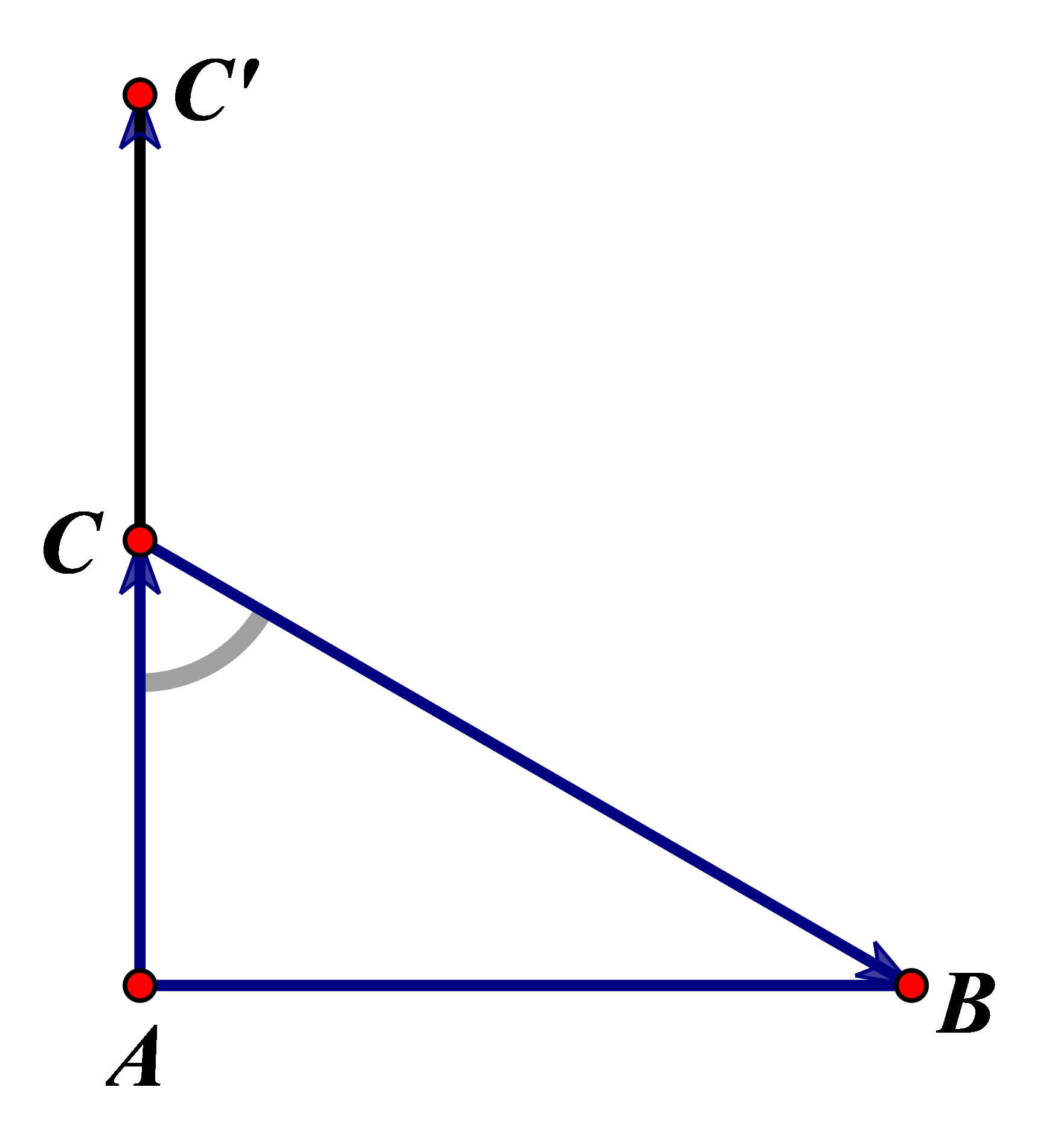
Ta có $(\overrightarrow{AC},\overrightarrow{CB}) = (\overrightarrow{CC$ $(\overrightarrow{AC},\overrightarrow{CB}) = (\overrightarrow{CC'},\overrightarrow{CB}) = \widehat{C'CB}$.

Do đó $cos(\overrightarrow{AC},\overrightarrow{CB}) = \cos\widehat{C$ $cos(\overrightarrow{AC},\overrightarrow{CB}) = \cos\widehat{C'CB} = - \cos\widehat{BCA} = - \frac{AC}{BC} = - \frac{1}{2}$.

Bài tập 3: Trong mặt phẳng toạ độ $Oxy$, cho $A( - 2;5),B( - 4; - 2),C(1;5)$. Tính số đo góc $\widehat{ACB}$ $\widehat{ACB}$?

Hướng dẫn giải

Ta có:

$AB = \sqrt{( - 2)^{2} + ( - 7)^{2}} = \sqrt{53}$ $AB = \sqrt{( - 2)^{2} + ( - 7)^{2}} = \sqrt{53}$

$AC = \sqrt{\lbrack 1 - ( - 2)\rbrack^{2} + (5 - 5)^{2}} = 3$ $AC = \sqrt{\lbrack 1 - ( - 2)\rbrack^{2} + (5 - 5)^{2}} = 3$

$BC = \sqrt{\lbrack 1 - ( - 4)\rbrack^{2} + \lbrack 5 - ( - 2)\rbrack^{2}} = \sqrt{74}$ $BC = \sqrt{\lbrack 1 - ( - 4)\rbrack^{2} + \lbrack 5 - ( - 2)\rbrack^{2}} = \sqrt{74}$

Ta có: $\overrightarrow{AB} \cdot \overrightarrow{AC} = ( - 2) \cdot 3 + ( - 7) \cdot 0 = - 6$ $\overrightarrow{AB} \cdot \overrightarrow{AC} = ( - 2) \cdot 3 + ( - 7) \cdot 0 = - 6$.

Suy ra $\cos\widehat{BAC} =cos(\overrightarrow{AB},\overrightarrow{AC})$ $\cos\widehat{BAC} =cos(\overrightarrow{AB},\overrightarrow{AC})$ $= \frac{\overrightarrow{AB}\cdot \overrightarrow{AC}}{|\overrightarrow{AB}| \cdot|\overrightarrow{AC}|} = \frac{- 6}{\sqrt{53} \cdot 3} = -\frac{2\sqrt{53}}{53}$ $= \frac{\overrightarrow{AB}\cdot \overrightarrow{AC}}{|\overrightarrow{AB}| \cdot|\overrightarrow{AC}|} = \frac{- 6}{\sqrt{53} \cdot 3} = -\frac{2\sqrt{53}}{53}$ nên $\widehat{BAC} \approx 106^{0}$ $\widehat{BAC} \approx 106^{0}$.

Ta có: $\overrightarrow{BA} \cdot \overrightarrow{BC} = 2.5 + 7.7 = 59$ $\overrightarrow{BA} \cdot \overrightarrow{BC} = 2.5 + 7.7 = 59$.

Suy ra $\cos\widehat{ABC} =cos(\overrightarrow{BA},\overrightarrow{BC})$ $\cos\widehat{ABC} =cos(\overrightarrow{BA},\overrightarrow{BC})$ $= \frac{\overrightarrow{BA}\cdot \overrightarrow{BC}}{|\overrightarrow{BA}| \cdot|\overrightarrow{BC}|} = \frac{59}{\sqrt{53} \cdot \sqrt{74}}$ $= \frac{\overrightarrow{BA}\cdot \overrightarrow{BC}}{|\overrightarrow{BA}| \cdot|\overrightarrow{BC}|} = \frac{59}{\sqrt{53} \cdot \sqrt{74}}$ nên $\widehat{ABC} \approx 20^{0}$ $\widehat{ABC} \approx 20^{0}$.

Vậy $\widehat{ACB} = 180^{{^\circ}} - (\widehat{BAC} + \widehat{ABC}) \approx 180^{{^\circ}} - \left( 106^{{^\circ}} + 20^{{^\circ}} \right) = 54^{{^\circ}}$ $\widehat{ACB} = 180^{{^\circ}} - (\widehat{BAC} + \widehat{ABC}) \approx 180^{{^\circ}} - \left( 106^{{^\circ}} + 20^{{^\circ}} \right) = 54^{{^\circ}}$.

Bài tập 4: Trong mặt phẳng tọa độ $Oxy$, cho các vectơ $\overrightarrow{a} = (2;5),\overrightarrow{b} = (3; - 7)$ $\overrightarrow{a} = (2;5),\overrightarrow{b} = (3; - 7)$, $\overrightarrow{c} = (1;1)$ $\overrightarrow{c} = (1;1)$.

a) Tính góc giữa hai vectơ $\overrightarrow{a},\overrightarrow{b}$ $\overrightarrow{a},\overrightarrow{b}$.

b) Tính góc giữa hai vectơ $\overrightarrow{a},\overrightarrow{c}$ $\overrightarrow{a},\overrightarrow{c}$.

c) Để $\overrightarrow{d} = (4x + 1)\overrightarrow{i} + (x + 4)\overrightarrow{j}$ $\overrightarrow{d} = (4x + 1)\overrightarrow{i} + (x + 4)\overrightarrow{j}$ tạo với vectơ $\overrightarrow{c}$ $\overrightarrow{c}$ một góc $45{^\circ}$ $45{^\circ}$ thì giá trị của x bằng bao nhiêu?

Hướng dẫn giải

a) Ta có:

$cos(\overrightarrow{a},\overrightarrow{b}) =\frac{\overrightarrow{a} \cdot \overrightarrow{b}}{|\overrightarrow{a}|\cdot |\overrightarrow{b}|}$ $cos(\overrightarrow{a},\overrightarrow{b}) =\frac{\overrightarrow{a} \cdot \overrightarrow{b}}{|\overrightarrow{a}|\cdot |\overrightarrow{b}|}$ $= \frac{2.3 + 5( - 7)}{\sqrt{2^{2} + 5^{2}}\cdot \sqrt{3^{2} + ( - 7)^{2}}} = - \frac{\sqrt{2}}{2}$ $= \frac{2.3 + 5( - 7)}{\sqrt{2^{2} + 5^{2}}\cdot \sqrt{3^{2} + ( - 7)^{2}}} = - \frac{\sqrt{2}}{2}$

$\Rightarrow(\overrightarrow{a},\overrightarrow{b}) =135^{0}$ $\Rightarrow(\overrightarrow{a},\overrightarrow{b}) =135^{0}$.

$cos(\overrightarrow{a},\overrightarrow{c}) =\frac{\overrightarrow{a} \cdot \overrightarrow{c}}{|\overrightarrow{a}|\cdot |\overrightarrow{c}|}$ $cos(\overrightarrow{a},\overrightarrow{c}) =\frac{\overrightarrow{a} \cdot \overrightarrow{c}}{|\overrightarrow{a}|\cdot |\overrightarrow{c}|}$ $= \frac{2.1 + 5.1}{\sqrt{2^{2} + 5^{2}}\cdot \sqrt{1^{2} + 1^{2}}} = \frac{7\sqrt{58}}{58}$ $= \frac{2.1 + 5.1}{\sqrt{2^{2} + 5^{2}}\cdot \sqrt{1^{2} + 1^{2}}} = \frac{7\sqrt{58}}{58}$

$\Rightarrow(\overrightarrow{a},\overrightarrow{c}) \approx23,1986^{0}$ $\Rightarrow(\overrightarrow{a},\overrightarrow{c}) \approx23,1986^{0}$

b) Ta có: $\overrightarrow{d} = (4x + 1;x + 4)$ $\overrightarrow{d} = (4x + 1;x + 4)$ tạo với $\overrightarrow{c}$ $\overrightarrow{c}$ một góc $45^{0}$ $45^{0}$ nên:

$cos(\overrightarrow{d},\overrightarrow{c}) =\frac{\overrightarrow{d} \cdot \overrightarrow{c}}{|\overrightarrow{d}|\cdot |\overrightarrow{c}|}$ $cos(\overrightarrow{d},\overrightarrow{c}) =\frac{\overrightarrow{d} \cdot \overrightarrow{c}}{|\overrightarrow{d}|\cdot |\overrightarrow{c}|}$ $= \frac{4x + 1 + x + 4}{\sqrt{2} \cdot\sqrt{(4x + 1)^{2} + (x + 4)^{2}}} = cos45^{0}$ $= \frac{4x + 1 + x + 4}{\sqrt{2} \cdot\sqrt{(4x + 1)^{2} + (x + 4)^{2}}} = cos45^{0}$

$\Leftrightarrow \frac{5x + 5}{\sqrt{2} \cdot \sqrt{17x^{2} + 16x + 17}} = \frac{\sqrt{2}}{2}$ $\Leftrightarrow \frac{5x + 5}{\sqrt{2} \cdot \sqrt{17x^{2} + 16x + 17}} = \frac{\sqrt{2}}{2}$

$\Leftrightarrow 5x + 5 = \sqrt{17x^{2} + 16x + 17}$ $\Leftrightarrow 5x + 5 = \sqrt{17x^{2} + 16x + 17}$

$\Leftrightarrow \left\{ \begin{matrix} x \geq - 1 \\ 17x^{2} + 16x + 17 = 25x^{2} + 50x + 25 \end{matrix} \right.$ $\Leftrightarrow \left\{ \begin{matrix} x \geq - 1 \\ 17x^{2} + 16x + 17 = 25x^{2} + 50x + 25 \end{matrix} \right.$

$\Leftrightarrow \left\{ \begin{matrix} x \geq - 1 \\ 8x^{2} + 34x + 8 = 0 \end{matrix} \Leftrightarrow x = - \frac{1}{4}. \right.$ $\Leftrightarrow \left\{ \begin{matrix} x \geq - 1 \\ 8x^{2} + 34x + 8 = 0 \end{matrix} \Leftrightarrow x = - \frac{1}{4}. \right.$

------------------------------------------------

Qua bài viết này, bạn đã nắm được cách tính góc giữa hai vectơ và các công thức cần thiết để áp dụng vào các bài toán Toán học lớp 10. Việc hiểu rõ công thức và phương pháp giải sẽ giúp bạn không chỉ vượt qua các bài kiểm tra mà còn phát triển tư duy toán học một cách toàn diện. Đừng quên luyện tập với các bài toán có đáp án để củng cố kiến thức và kỹ năng tính toán của mình. Chúc bạn học tốt và đạt kết quả cao trong học tập!

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

30 lượt tải tài liệu

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi:
Bơ

1

34

Bài trước

Bài sau

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!