Đề thi giáo viên dạy giỏi môn Toán cấp THCS phòng GD&ĐT Thái Hòa, Nghệ An năm 2015 - 2016

Đề thi giáo viên dạy giỏi môn Toán cấp THCS

Đề thi giáo viên dạy giỏi môn Toán cấp THCS phòng GD&ĐT Thái Hòa, Nghệ An năm 2015 - 2016 có đáp án là tài liệu tham khảo hữu ích dành cho quý thầy cô được VnDoc sưu tầm và giới thiệu giúp các thầy cô ôn lại kiến thức để chuẩn bị sẵn sàng cho kỳ thi đánh gia năng lực giáo viên cấp tỉnh.

Đề thi giáo viên dạy giỏi môn Địa lý cấp THCS tỉnh Vĩnh Phúc năm 2015 - 2016

Đề thi giáo viên dạy giỏi môn Toán cấp THCS phòng GD&ĐT Yên Thành, Nghệ An năm 2015 - 2016

Câu 1: (5,0 điểm)

a) Nêu các bước để xây dựng phân phối chương trình môn học mà thầy (cô) đang giảng dạy?

b) Nêu một số khó khăn cần khắc phục khi đổi mới sinh hoạt chuyên môn theo nghiên cứu bài học?

Câu 2: (6,0 điểm)

a) Hãy trình bày cụ thể con đường khi dạy định lý Vi - ét trong sách giáo khoa toán 9 hiện hành. Vận dụng định lý Vi - ét hãy giải bài toán sau:

Cho phương trình x² + (m² + 1). x + m = 2 (với m là tham số)

Hãy tìm giá trị của m để phương trình có hai nghiệm x₁; x₂ thỏa mãn

b) Hãy nêu hai định hướng để học sinh tìm ra cách giải bài toán sau và hướng dẫn học sinh giải bài toán theo một trong hai cách đã định hướng. Cho A(n) = n⁵ – n (với n là số nguyên). Chứng minh A(n) chia hết cho 30

Câu 3: (4,0 điểm)

Một học sinh có lời giải của một bài toán như sau: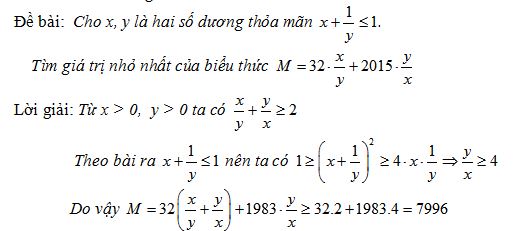

Đẳng thức xảy ra khi và chỉ khi x = y

Vậy giá trị nhỏ nhất của M là 7996

Thầy (cô) hãy chỉ ra các sai lầm trong lời giải trên và giải lại cho đúng.

Câu 4: (5,0 điểm)

Cho nửa đường tròn (O), đường kính AB = 2R và M là một điểm bất kỳ thuộc nửa đường tròn (M khác A và B). Tiếp tuyến tại M cắt các tiếp tuyến Ax và By tại A và B của đường tròn (O) lần lượt tại C và D.

a) Chứng minh: ∠COD = 90^o

b) Gọi K là giao điểm của BM với Ax. Chứng minh: ΔKMO ~ ΔAMD

c) Tìm giá trị nhỏ nhất của tổng diện tích hai tam giác ACM và BDM.

1. Thầy (cô) hãy giải bài toán trên.

2. Hãy xây dựng và chứng minh bài toán đảo của bài toán ở câu a?

Đáp án đề thi giáo viên dạy giỏi môn Toán cấp THCS

Câu 1:

a) Bước 1: Xác định nguyên tắc xây dưng phân phối chương trình môn học

Bước 2: Nghiên cứu thực hiện

Bước 3: Xây dựng kế hoạch dạy học cho mỗi môn học/ lớp học theo định hướng mới.

Bước 4: Duyệt của hiệu trưởng

Bước 5: Đánh giá kết quả, rút kinh nghiệm, bổ sung

Bước 6: Thực hiện

b) Thái độ của GV đối với SHCM: nhiều GV hoài nghi về tác dụng chuyên môn và sợ các đồng nghiệp tấn công mình.

Tiến hành bài học minh hoạ: GV dạy như là diễn tập và không để ý đến HS gặp khó khăn như thế nào.

Dự giờ bài học: các GV dự chỉ chú ý đến GV dạy và họ thích ngồi ở đằng sau và ít chú ý đến HS.

Suy ngẫm về bài học: có nhiều GV có thái độ phê phán người dạy, hay ca ngợi rõ ràng nhưng không chi tiết.

Các GV chưa thực sự hợp tác cùng nhau xây dựng kế hoạch bài học.

Thái độ của GV không phải là hoà đồng, bình đẳng, sẵn sàng học hỏi, hợp tác mà lại là phê phán, đánh giá, làm mất đi tính nhân văn của NCBH.

Câu 2:

a) Nêu trình tự các hoạt động cụ thể theo một trong hai con đường

• Con đường có khâu suy đoán: Tạo động cơ; phát hiện định lí; phát biểu định lý; chứng minh định lí; vận dụng định lý
• Con đường suy diễn: Tạo động cơ; suy luận logic dẫn tới định lý; phát biểu định lý; củng cố định lý

Vận dụng giải bài tập toán:

Vì với mọi m

Nên phương trình đã cho luôn có 2 nghiệm phân biệt x₁; x₂ với mọi m.