Đề thi học sinh giỏi thành phố Đà Nẵng môn Toán lớp 10 năm học 2010 - 2011 (Có đáp án)
Đề thi học sinh giỏi lớp 10 môn Toán có đáp án
Đề thi học sinh giỏi thành phố Đà Nẵng môn Toán lớp 10 năm học 2010 - 2011 (Có đáp án) dưới đây sẽ giúp các bạn học sinh ôn thi học sinh giỏi, thi học kì 2 lớp 10 dễ dàng hơn. Mời các bạn tải đề thi học sinh giỏi lớp 10 môn Toán này về và tham khảo.
| SỞ GIÁO DỤC VÀ ĐÀO TẠO THÀNH PHỐ ĐÀ NẴNG (Đề thi chính thức) | KỲ THI CHỌN HỌC SINH GIỎI LỚP 10 NĂM HỌC: 2010 - 2011 Môn: TOÁN Thời gian: 150 phút (không kể thời gian giao đề) |
Câu I (1,5 điểm)
1) Xác định tính chẵn - lẻ của hàm số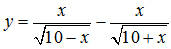 
2) Cho các nửa khoảng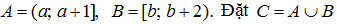 
Với điều kiện nào của các số thực a và b thì C là một đoạn? Tính độ dài của đoạn C khi đó.
Câu II (2,0 điểm)
1) Tìm m để phương trình |x2 - 1| = m4 - m2 + 1 có bốn nghiệm phân biệt.
2) Giải và biện luận (theo tham số m) bất phương trình: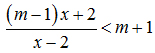 
Câu III (2,5 điểm)
1) Giải phương trình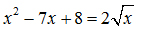 
2) Giải hệ phương trình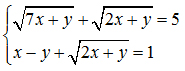 
Câu IV (3,0 điểm)
1) Cho tam giác ABC có AB = c, AC = b và Các điểm M, N được xác định bởi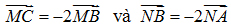 
.Tìm hệ thức liên hệ giữa b và c để AM và CN vuông góc với nhau.
2) Cho tam giác ABC. Trên các cạnh BC, CA và AB của tam giác đó, lần lượt lấy các điểm và Gọi và S tương ứng là diện tích của các tam giác và ABC. Chứng minh bất đẳng thức 
.Dấu đẳng thức xảy ra khi và chỉ khi nào?
Câu V (1,0 điểm)
Trong mặt phẳng tọa độ Oxy, cho đường tròn tâm O bán kính R (R > 0, R không đổi). Gọi A và B lần lượt là các điểm di động trên trục hoành và trục tung sao cho đường thẳng AB luôn tiếp xúc với đường tròn đó. Hãy xác định tọa độ của các điểm A, B để tam giác OAB có diện tích nhỏ nhất.
