Đề thi khảo sát chất lượng thi Đại học tỉnh Vĩnh Phúc môn Toán khối A, A1

Đề thi thử đại học môn Toán

SỞ GIÁO DỤC VÀ ĐÀO TẠO VĨNH PHÚC

KỲ KSCL THI ĐẠI HỌC NĂM HỌC 2012-2013 LẦN 1 ĐỀ THI MÔN: TOÁN - KHỐI A, A1 Thời gian làm bài: 180 phút (không kể thời gian giao đề)

I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7,0 điểm)

Câu 1 (2,0 điểm) Cho hàm số , có đồ thị là (C).

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.

b) Viết phương trình tiếp tuyến d của đồ thị (C), biết tiếp tuyến d tạo với trục Ox một góc α sao cho .

Câu 2 (1,0 điểm)

Giải phương trình:

Câu 3 (1,0 điểm)

Giải hệ phương trình: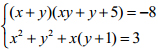

Câu 4 (1,0 điểm)

Tìm tất cả các giá trị của m để phương trình: có hai nghiệm thực phân biệt.

Câu 5 (1,0 điểm)

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) trùng với trọng tâm tam giác ABD. Cạnh SD tạo với đáy (ABCD) một góc bằng 60^o. Tính thể tích khối chóp S.ABCD và khoảng cách từ A tới mặt phẳng (SBC) theo a.

Câu 6 (1,0 điểm)

Tìm tất cả các giá trị thực của m để với mọi x thuộc ta đều có: tan⁸x + cotg⁸x ≥ m + 64cos²2x.

II. PHẦN RIÊNG (3,0 điểm)

Thí sinh chỉ được làm một trong hai phần (phần A hoặc phần B)

A. Theo chương trình Chuẩn

Câu 7.a (1,0 điểm) Cho đường tròn (C): x² + y² - 4x + 6y - 12 = 0 và điểm M(2; 4 3). Viết phương trình đường thẳng d cắt đường tròn (C) tại hai điểm A, B sao cho tam giác MAB đều.

Câu 8.a (1,0 điểm) Tìm hệ số của x⁴ trong khai triển thành đa thức của biểu thức: (1 + x + 4x²)¹⁰

Câu 9.a (1,0 điểm) Giải phương trình:

B. Theo chương trình Nâng cao

Câu 7.b (1,0 điểm) Cho elíp và điểm I(1; 1). Viết phương trình đường thẳng d qua I cắt (E) tại hai điểm M, N sao cho I là trung điểm của MN.

Câu 8.b (1,0 điểm) Tính giới hạn:

Câu 9.b (1,0 điểm)

Có tất cả bao nhiêu số tự nhiên có 5 chữ số khác nhau mà trong mỗi số đó luôn có mặt hai chữ số lẻ và ba chữ số chẵn.