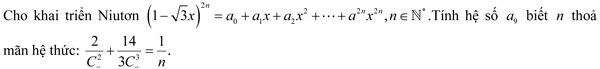Đề thi thử Đại học môn Toán khối B, D năm 2013 - Trường THPT chuyên Vĩnh Phúc

PHẦN CHUNG CHO TẤT CẢ THÍ SINH (8,0 điểm)

Câu I. (2,5 điểm) Cho hàm số y = -x³ - 3x² + 4 ⁽¹⁾
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1)
2. Với những giá trị nào của m thì đường thẳng nối hai cực trị đồ thị của hàm số (1) tiếp xúc với đường tròn (C): (x-m)² + (y-m-1)² = 5

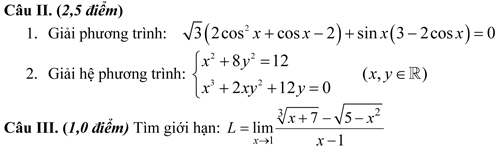
Câu IV. (1,0 điểm)
Cho tứ diện ABCD có AD vuông góc với mặt phẳng (ABC), AD = 3a; AB = 2a; AC = 4a; Góc BAC = 60⁰.Gọi H, K lần lượt là hình chiếu vuông góc của B trên AC và CD. Đường thẳng HK cắt đường thẳng AD tại E. Chứng minh rằng BE vuông góc với CD và tính thể tích khối tứ diện BCDE theo a.

Câu V. (1,0 điểm)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số

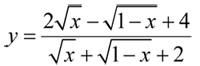
PHẦN RIÊNG (2,0 điểm). Thí sinh chỉ được làm một trong hai phần (phần A hoặc B)

A. Theo chương trình Chuẩn

Câu VI.a. (1,0 điểm) Cho tam giác ABC có B(2;1), đường thẳng chứa cạnh AC có phương trình: 2x + y + 1 = 0, đường thẳng chứa trung tuyến AM có phương trình: 3x + 2y + 3 = 0. Tính diện tích của tam giác ABC

Câu VII.a. (1,0 điểm) Tính tổng: S = C⁰₂₀₁₂ + 2C¹₂₀₁₂ + 3C²₂₀₁₂ + 4C³₂₀₁₂ + ... + 2013C²⁰¹²₂₀₁₂

B. Theo chương trình Nâng cao

Câu VI.a. (1,0 điểm) Trong mặt phẳng với hệ trục toạ độ Oxy , cho điểm E(1;0) và đường tròn (C): x 2 + y2 - 8x - 4y - 16 = 0. Viết phương trình đường thẳng đi qua điểm E cắt đường tròn (C) theo dây cung MN có độ dài ngắn nhất.

Câu VIIb. (1,0 điểm)