Đề thi tuyển sinh lớp 10 THPT chuyên Nguyễn Trãi, Hải Dương - Môn Toán (2010 - 2011)

Để chuẩn bị cho kỳ thi vào cấp 3 sắp tới, Vndoc.com xin gửi đến các bạn: Đề thi tuyển sinh lớp 10 THPT chuyên Nguyễn Trãi, Hải Dương - Môn Toán (2010 - 2011).

Đề thi tuyển sinh lớp 10 môn Toán:

SỞ GIÁO DỤC VÀ ĐÀO TẠO HẢI DƯƠNG (Đề thi chính thức)

KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN NGUYỄN TRÃI NĂM HỌC 2010-2011 KHÓA NGÀY 08/07/2010 Môn thi: TOÁN (Dành cho thí sinh thi vào lớp chuyên Toán) Thời gian làm bài: 150 phút (không kể thời gian giao đề)

Câu 1 (2,0 điểm)

1) Cho: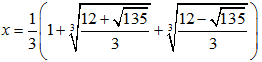

Không dùng máy tính cầm tay, hãy tính giá trị của biểu thức: M = (9x³ - 9x² - 3)²

2) Cho trước a,b thuộc R; gọi x, y là hai số thực thỏa mãn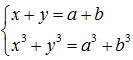

Chứng minh rằng: x²⁰¹¹ + y ²⁰¹¹ = s²⁰¹¹ + b²⁰¹¹

Câu 2 (2,0 điểm)

Cho phương trình: x³ + ax² + bx - 1 = 0 (1)

1) Tìm các số hữu tỷ a và b để phương trình (1) có nghiệm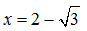

2) Với giá trị a, b tìm được ở trên; gọi x₁, x₂, x₃ là ba nghiệm của phương trình (1). Tính giá trị của biểu thức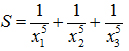

Câu 3 (2,0 điểm)

1) Tìm các số nguyên x, y thỏa mãn điều kiện: x² + y² + 5x²y² + 6 = 37xy

2) Giải hệ phương trình: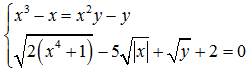

Câu 4 (3,0 điểm)

Cho hai đường tròn (O ; R) và (O’ ; R’) cắt nhau tại I và J (R’ > R). Kẻ các tiếp tuyến chung của hai đường tròn đó; chúng cắt nhau ở A. Gọi B và C là các tiếp điểm của hai tiếp tuyến trên với (O’ ; R’); D là tiếp điểm của tiếp tuyến AB với (O ; R) (điểm I và điểm B ở cùng nửa mặt phẳng bờ là O’A). Đường thẳng AI cắt (O’ ; R’) tại M (điểm M khác điểm I).

1) Gọi K là giao điểm của đường thẳng IJ với BD. Chứng minh: ; từ đó suy ra KB = KD.

2) AO’ cắt BC tại H. Chứng minh 4 điểm I, H, O’, M nằm trên một đường tròn.

3) Chứng minh đường thẳng AM là tiếp tuyến của đường tròn ngoại tiếp tam giác IBD.

Câu 5 (1,0 điểm)

Mọi điểm trên mặt phẳng được đánh dấu bởi một trong hai dấu (+) hoặc ().

Chứng minh rằng luôn chỉ ra được 3 điểm trên mặt phẳng làm thành tam giác vuông cân mà ba đỉnh của nó được đánh cùng dấu.