Đề thi tuyển sinh lớp 10 THPT tỉnh Đăk Nông năm 2011 - 2012 môn Toán (chuyên) - Có đáp án

Nhằm giúp các bạn chuẩn bị thật tốt kiến thức để làm bài thi đạt hiệu quả cao, Vndoc.com xin giới thiệu: Đề thi tuyển sinh lớp 10 THPT tỉnh Đăk Nông năm 2011 - 2012 môn Toán (chuyên) - Có đáp án.

Đề thi tuyển sinh lớp 10 môn Toán (chuyên):

SỞ GIÁO DỤC VÀ ĐÀO TẠO TỈNH ĐẮK NÔNG (Đề thi chính thức)

KÌ THI TUYỂN SINH VÀO LỚP 10 THPT Khóa ngày 22 tháng 6 năm 2011

MÔN THI: TOÁN(Chuyên)
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
--------------------------------------------------------------------------------

Câu 1: (2,0 điểm)

a. Giải phương trình: x⁴ - 7x² -+ 12 = 0

b. Giải hệ phương trình: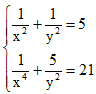

Câu 2: (2,0 điểm)

Cho biểu thức: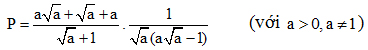

a. Rút gọn P.

b. Tính giá trị biểu thức P biết

Câu 3: (2,0 điểm)

Cho parabol (P): và đường thẳng (d): y = mx + 3, (m là tham số).

a. Chứng minh rằng (d) luôn cắt (P) tại 2 điểm phân biệt I, J với mọi m.

b. Xác định m để tam giác OIJ cân tại O (O là gốc tọa độ).

Câu 4: (3,0 điểm)

Cho AB = 3a, trên đoạn thẳng AB lấy điểm C sao cho . Hai đường thẳng qua A tiếp xúc với đường tròn tâm O đường kính BC lần lượt tại P và Q.

a. Chứng minh tứ giác OPAQ nội tiếp.

b. Kéo dài OP cắt đường tròn (O) tại E. Chứng minh rằng tứ giác OBEQ là hình thoi.

c. Trên tia đối của tia BA lấy điểm M. Đặt BM = x. ME cắt AQ tại N. Xác định x theo a để tam giác EQN có diện tích bằng .

Câu 5: (1,0 điểm)

Giả sử phương trình: ax² + bx + c = 0 có 2 nghiệm x₁, x₂ và phương trình cx² + bx + a = 0 có 2 nghiệm x₃, x₄.

Chứng minh rằng: