Đề thi tuyển sinh lớp 10 THPT tỉnh Hải Phòng năm học 2012 - 2013 môn Toán (Có đáp án)

Đề chuẩn bị cho kỳ thi vào cấp 3 sắp tới, Vndoc.com xin gửi đến các bạn: Đề thi tuyển sinh lớp 10 THPT tỉnh Hải Phòng năm học 2012 - 2013 môn Toán (Có đáp án).

Đề thi tuyển sinh vào lớp 10 môn Toán:

Phần I: Trắc nghiệm (2,0 điểm) Hãy chọn chỉ 1 chữ cái đứng trước câu trả lời đúng

Câu 1: Điều kiện xác định của biểu thức là:
A. x ≥ 1 B. x = 1 C. x ≤ 1 D. x ≤ 1 và x # 0

Câu 2: Điểm thuộc đồ thị hàm số y = x/2 + 1 là:
A(2; -1/2) B.(2; 2) C. (0; -1) D. (-2; -1)

Câu 3: Nghiệm của hệ phương trình là:
A(-3; -1) B. (1; -1) C. (1; 1) D.(1; -2)

Câu 4: Phương trình (2m - 1)x² - mx - 1 = 0 là phương trình bậc hai ẩn x khi:
A. m # 1/2 B. m # 1 C. m # 2 D. m # -1

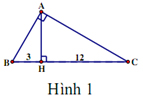
Câu 5: Tam giác ABC vuông tại A, AH vuông góc BC, BH = 3, CH = 12 (hình 1). Độ dài đoạn thẳng AH là:
A. 8 B. 12 C. 25 D. 6

Câu 6: Tam giác MNP vuông tại M biết MN = 3a, MP = 3√3a. Khi đó tanP bằng:

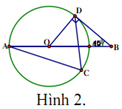
Câu 7: Trong hình 2, biết góc DBA = 40^o, số đo góc ACD bằng
A. 60^o B. 130^o C. 70^o D. 65^o

Câu 8: Cho hình chữ nhật ABCD có AB = 4cm, BC = 3cm. Quay hình chữ nhật đó xung quanh AB ta được một hình trụ. Thể tích của hình trụ đó bằng:
A. 36πcm³ B. 48πcm³ C. 24πcm³ D. 64πcm³

Phần II: Phần tự luận (8,0 điểm)

Bài 1: (1,5 điểm)

1. Rút gọn các biểu thức sau:

2. Xác định hàm số y = (a + 1)x², biết đồ thị hàm số đi qua điểm A(1; -2)

Bài 2: (2,5 điểm)

1. Giải phương trình: x² + 2x - 3 = 0

2. Cho phương trình: x² + mx - m - 1 = 0 (1) (m là tham số)

a. Chứng minh rằng với mọi m phương trình (1) luôn có nghiệm

b. Tìm các giá trị của m để phương trình (1) có ít nhất một nghiệm không dương.

3. Tìm hai số biết tổng của chúng bằng 8 và số thứ nhất gấp 3 lần số thứ hai.

Bài 3: (3,0 điểm)

Cho tam giác ABC có ba góc nhọn và AB = AC. Đường tròn tâm O đường kính AB = 2R cắt các cạnh BC, AC lần lượt tại I, K. Tiếp tuyến của đường tròn (O) tại B cắt AI tại D, H là giao điểm của AI và BK.

a. Chứng minh tứ giác IHKC nội tiếp

b. Chứng minh BC là tia phân giác của góc DBH và tứ giác BDCH là hình thoi.

c. Tính diện tích hình thoi BDCH theo R trong trường hợp tam giác ABC đều.

Bài 4: (1,0 điểm)

1. Cho x > 0, y > 0. Chứng minh rằng . Dấu "=" xảy ra khi nào?

2. Cho x > 0, y > 0 và 2x + 3y ≤ 2. Tìm giá trị nhỏ nhất của biểu thức: