Đề thi tuyển sinh lớp 10 THPT tỉnh Hải Phòng năm học 2013 - 2014 môn Toán (Có đáp án)

Nhằm giúp các bạn chuẩn bị thật tốt kiến thức để làm bài thi đạt hiệu quả cao, Vndoc.com xin giới thiệu: Đề thi tuyển sinh lớp 10 THPT tỉnh Hải Phòng năm học 2013 - 2014 môn Toán (Có đáp án).

Đề thi tuyển sinh lớp 10 môn Toán:

SỞ GIÁO DỤC VÀ ĐÀO TẠO HẢI PHÒNG ĐỀ THI CHÍNH THỨC

KÌ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2013 - 2014 MÔN THI: TOÁN Thời gian làm bài: 120 phút (không kể thời gian giao đề)

Phần I. Trắc nghiệm khách quan (2,0 điểm)

Hãy chọn chỉ một chữ cái đứng trước câu trả lời đúng.

Câu 1: Điều kiện xác định của biểu thức là:

Câu 2: Nếu điểm A(1;-2) thuộc đường thẳng (d): y = 5x + m thì m bằng:
A. -7; B. 11; C. -3; D. 3.

Câu 3: Phương trình nào sau đây có nghiệm kép?
A. x² - x = 0; B. 3x² + 2 = 0; C. 3x² + 2x + 1 = 0; D. 9x² + 12x + 4 = 0.

Câu 4: Hai số -5 và 3 là nghiệm của phương trình nào sau đây ?
A. x² + 2x + 15 = 0; B. x² - 2x - 15 = 0;
C. x² + 2x - 15 = 0; D. x² - 8x + 15 = 0.

Câu 5: Cho ΔABC vuông tại A có AH vuông góc BC, AB = 8, BH = 4 (hình 1). Độ dài cạnh BC bằng
A. 24; B. 32; C. 18; D. 16.

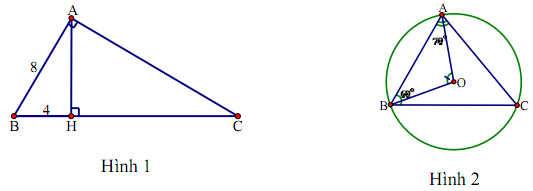
Câu 6: Cho tam giác ABC có góc BAC = 70^o, góc BAC = 60^o nội tiếp đường tròn tâm O (hình 2). Số đo của góc AOB bằng
A. 50⁰; B. 100⁰; C. 120⁰; D. 140⁰.

Câu 7: Cho tam giác ABC vuông tại A có góc ABC = 30^o, BC = a. Độ dài cạnh AB bằng:

Câu 8: Một hình trụ có chiều cao bằng hai lần đường kính đáy. Nếu đường kính đáy có chiều dài bằng 4cm thì thể tích của hình trụ đó bằng
A. 16πcm³; B. 32 πcm³; C. 64πcm³ D. 128πcm³

Phần II. Tự luận (8,0 điểm)

Bài 1: (1,5 điểm)

1. Rút gọn các biểu thức sau:

2. Cho đường thẳng (d): y = 4x – 3 và parabol (P): y = x². Tìm tọa độ giao điểm của (d) và (P) bằng phép toán.

Bài 2. (2,5 điểm)

1. Giải bất phương trình:

2. Cho hệ phương trình: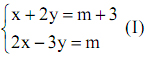

a) Giải hệ phương trình (I) khi m = 1.

b) Tìm m để hệ (I) có nghiệm duy nhất (x ; y) thỏa mãn x + y = -3.

3. Một khu vườn hình chữ nhật có chiều dài lớn hơn chiều rộng 3m và diện tích bằng 270m². Tìm chiều dài, chiều rộng của khu vườn.

Bài 3. (3,0 điểm)

Cho tam giác nhọn ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại H (D thuộc BC, E thuộc AC, F thuộc AB)

1. Chứng minh các tứ giác BDHF, BFEC nội tiếp.

2. Đường thẳng EF cắt đường tròn (O) tại M và N (F nằm giữa M và E). Chứng minh cung AM = cung AN.

3. Chứng minh AM là tiếp tuyến của đường tròn ngoại tiếp tam giác MHD.

Bài 4. (1,0 điểm)

1. Cho x, y là các số dương. Chứng minh rằng: . Dấu "=" xảy ra khi nào?

2. Tìm cặp số (x, y) thỏa mãn