Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Giải SBT Toán 6 Bài 2: Tính chất cơ bản của phân số

Giải sách bài tập Toán lớp 6 Chân trời sáng tạo

Giải sách bài tập Toán lớp 6 Bài 2: Tính chất cơ bản của phân số. Toàn bộ bài tập hệ thống lại chương trình học trên lớp. Các đáp án dưới đây bám sát chương trình học SGK, mời các em học sinh cùng tham khảo.

>> Bài trước: Giải SBT Toán 6 Bài 1: Phân số với tử số và mẫu số là số nguyên

Bài 1 trang 11 SBT Toán 6 tập 2

Quy đồng mẫu số các phân số sau:

a) $\frac{{11}}{{ - 12}}và \frac{{ - 17}}{{18}}$ $\frac{{11}}{{ - 12}}và \frac{{ - 17}}{{18}}$;

b) $\frac{{ - 9}}{{15}}và \frac{{17}}{{ - 20}}$ $\frac{{ - 9}}{{15}}và \frac{{17}}{{ - 20}}$;

c) $\frac{{ - 5}}{6};\frac{{ - 2}}{5}và \frac{7}{{ - 12}}$ $\frac{{ - 5}}{6};\frac{{ - 2}}{5}và \frac{7}{{ - 12}}$ ;

Đáp án

a) Chọn mẫu số chung là 36

Ta thực hiện $\frac{{11}}{{ - 12}} = \frac{{11.( - 3)}}{{ - 12.( - 3)}} = \frac{{ - 33}}{{36}}$ $\frac{{11}}{{ - 12}} = \frac{{11.( - 3)}}{{ - 12.( - 3)}} = \frac{{ - 33}}{{36}}$ và $\frac{{ - 17}}{{18}} = \frac{{ - 17.2}}{{18.2}} = \frac{{ - 34}}{{36}}$ $\frac{{ - 17}}{{18}} = \frac{{ - 17.2}}{{18.2}} = \frac{{ - 34}}{{36}}$;

b) Chọn mẫu số chung là 60

Ta thực hiện $\frac{{ - 9}}{{15}} = \frac{{ - 9.4}}{{15.4}} = \frac{{ - 36}}{{60}}$ $\frac{{ - 9}}{{15}} = \frac{{ - 9.4}}{{15.4}} = \frac{{ - 36}}{{60}}$ và $\frac{{17}}{{ - 20}} = \frac{{17.( - 3)}}{{( - 20).( - 3)}} = \frac{{ - 51}}{{60}}$ $\frac{{17}}{{ - 20}} = \frac{{17.( - 3)}}{{( - 20).( - 3)}} = \frac{{ - 51}}{{60}}$;

c) Chọn mẫu số chung là 60

Ta thực hiện $\frac{{ - 5}}{6} = \frac{{ - 5.10}}{{6.10}} = \frac{{ - 50}}{{60}};\frac{{ - 2}}{5} = \frac{{ - 2.12}}{{5.12}} = \frac{{ - 24}}{{60}}$ $\frac{{ - 5}}{6} = \frac{{ - 5.10}}{{6.10}} = \frac{{ - 50}}{{60}};\frac{{ - 2}}{5} = \frac{{ - 2.12}}{{5.12}} = \frac{{ - 24}}{{60}}$

và $\frac{7}{{ - 12}} = \frac{{7.( - 5)}}{{\left( { - 12} \right).( - 5)}} = \frac{{ - 35}}{{60}}$ $\frac{7}{{ - 12}} = \frac{{7.( - 5)}}{{\left( { - 12} \right).( - 5)}} = \frac{{ - 35}}{{60}}$ ;

Bài 2 trang 12 SBT Toán 6 tập 2

Viết các số sau thành các phân số có cùng mẫu số (chọn mẫu số chung là số dương nhỏ nhất nếu được)

a) $- 5;\;\frac{{17}}{{ - 20}} và \frac{{ - 16}}{9}$ $- 5;\;\frac{{17}}{{ - 20}} và \frac{{ - 16}}{9}$;

b) $\frac{{13}}{{ - 15}};\;\frac{{ - 18}}{{25}}và - 3$ $\frac{{13}}{{ - 15}};\;\frac{{ - 18}}{{25}}và - 3$

Đáp án

a) Chọn mẫu số chung là 180

Ta thực hiện $- 5 = \frac{{ - 5}}{1} = \frac{{( - 5).180}}{{1.180}} = \frac{{ - 900}}{{180}};$ $- 5 = \frac{{ - 5}}{1} = \frac{{( - 5).180}}{{1.180}} = \frac{{ - 900}}{{180}};$

$\frac{{17}}{{ - 20}} = \frac{{17.( - 9)}}{{( - 20).( - 9)}} = \frac{{ - 153}}{{180}}$ $\frac{{17}}{{ - 20}} = \frac{{17.( - 9)}}{{( - 20).( - 9)}} = \frac{{ - 153}}{{180}}$

và $\frac{{ - 16}}{9} = \frac{{ - 16.20}}{{9.20}} = \frac{{ - 320}}{{180}}$ $\frac{{ - 16}}{9} = \frac{{ - 16.20}}{{9.20}} = \frac{{ - 320}}{{180}}$;

b) Chọn mẫu số chung là 75

Ta thực hiện

$\frac{{13}}{{ - 15}} = \frac{{13.( - 5)}}{{( - 15).( - 5)}} = \frac{{ - 65}}{{75}}$ $\frac{{13}}{{ - 15}} = \frac{{13.( - 5)}}{{( - 15).( - 5)}} = \frac{{ - 65}}{{75}}$;

$\frac{{ - 18}}{{25}} = \frac{{( - 18).3}}{{25.3}} = \frac{{ - 54}}{{75}}$ $\frac{{ - 18}}{{25}} = \frac{{( - 18).3}}{{25.3}} = \frac{{ - 54}}{{75}}$

và $- 3 = \frac{{ - 3}}{1} = \frac{{\left( { - 3} \right).75}}{{1.75}} = \frac{{ - 225}}{{75}}$ $- 3 = \frac{{ - 3}}{1} = \frac{{\left( { - 3} \right).75}}{{1.75}} = \frac{{ - 225}}{{75}}$

Bài 3 trang 12 SBT Toán 6 tập 2

a) $\frac{{390}}{{ - 240}}$ $\frac{{390}}{{ - 240}}$;

b) $\frac{{ - 60}}{{84}}$ $\frac{{ - 60}}{{84}}$;

c) $\frac{{6262}}{{ - 6666}}$ $\frac{{6262}}{{ - 6666}}$;

d) $\frac{{ - 2020}}{{2024}}$ $\frac{{ - 2020}}{{2024}}$;

Đáp án

a) $\frac{{390}}{{ - 240}} = \frac{{390:10}}{{ - 240:10}} = \frac{{39}}{{ - 24}} = \frac{{39:3}}{{ - 24:3}} = \frac{{13}}{{ - 8}}$ $\frac{{390}}{{ - 240}} = \frac{{390:10}}{{ - 240:10}} = \frac{{39}}{{ - 24}} = \frac{{39:3}}{{ - 24:3}} = \frac{{13}}{{ - 8}}$;

b) $\frac{{ - 60}}{{84}} = \frac{{ - 60:4}}{{84:4}} = \frac{{ - 15}}{{21}} = \frac{{ - 15:3}}{{21:3}} = \frac{{ - 5}}{7}$ $\frac{{ - 60}}{{84}} = \frac{{ - 60:4}}{{84:4}} = \frac{{ - 15}}{{21}} = \frac{{ - 15:3}}{{21:3}} = \frac{{ - 5}}{7}$

c) $\frac{{6262}}{{ - 6666}} = \frac{{6262:( - 101)}}{{ - 6666:( - 101)}} = \frac{{ - 62}}{{66}} = \frac{{ - 62:2}}{{66:2}} = \frac{{ - 31}}{{33}}$ $\frac{{6262}}{{ - 6666}} = \frac{{6262:( - 101)}}{{ - 6666:( - 101)}} = \frac{{ - 62}}{{66}} = \frac{{ - 62:2}}{{66:2}} = \frac{{ - 31}}{{33}}$

d) $\frac{{ - 2020}}{{2024}} = \frac{{ - 2020:4}}{{2024:4}} = \frac{{ - 505}}{{506}}$ $\frac{{ - 2020}}{{2024}} = \frac{{ - 2020:4}}{{2024:4}} = \frac{{ - 505}}{{506}}$

Bài 4 trang 12 SBT Toán 6 tập 2

Hình vẽ sau minh hoạ tính chất nào của phân số?

Hình vẽ sau minh hoạ tính chất nào của phân số

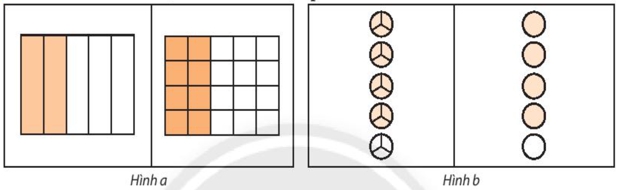
Đáp án

a) Ta có hai phân số là $\frac{2}{5}$ $\frac{2}{5}$ và $\frac{8}{{20}}$ $\frac{8}{{20}}$.

Vì $\frac{2}{5} = \frac{{2.4}}{{5.4}} = \frac{8}{{20}}$ $\frac{2}{5} = \frac{{2.4}}{{5.4}} = \frac{8}{{20}}$ nên hình a) mình hoạ tính chất 1 (Nếu nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho).

b) Ta có hai phân số là $\frac{{12}}{{15}}$ $\frac{{12}}{{15}}$và $\frac{4}{5}$ $\frac{4}{5}$.

Vì $\frac{{12}}{{15}} = \frac{{12:3}}{{15:3}} = \frac{4}{5}$ $\frac{{12}}{{15}} = \frac{{12:3}}{{15:3}} = \frac{4}{5}$nên hình b) mình hoạ tính chất 2 (Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số mới bằng phân số đã cho).

Bài 5 trang 12 SBT Toán 6 tập 2

Nêu hai cách giải thích các phân số sau bằng nhau (dùng khái niệm bằng nhau và dùng tính chất)

a) $\frac{{ - 15}}{{33}}và \frac{5}{{ - 11}}$ $\frac{{ - 15}}{{33}}và \frac{5}{{ - 11}}$;

b) $\frac{7}{{ - 12}} và \frac{{35}}{{ - 60}}$ $\frac{7}{{ - 12}} và \frac{{35}}{{ - 60}}$;

c) $\frac{{ - 8}}{{14}} và \frac{{12}}{{ - 21}}$ $\frac{{ - 8}}{{14}} và \frac{{12}}{{ - 21}}$

Đáp án

a) Cách 1: $\frac{{ - 15}}{{33}} = \frac{5}{{ - 11}}$ $\frac{{ - 15}}{{33}} = \frac{5}{{ - 11}}$ vì ( - 15).( - 11) = 33.5 = 165

Cách 2: $\frac{{ - 15}}{{33}} = \frac{{ - 15:( - 3)}}{{33:( - 3)}} = \frac{5}{{ - 11}}$ $\frac{{ - 15}}{{33}} = \frac{{ - 15:( - 3)}}{{33:( - 3)}} = \frac{5}{{ - 11}}$

b) Cách 1: $\frac{7}{{ - 12}} = \frac{{35}}{{ - 60}}$ $\frac{7}{{ - 12}} = \frac{{35}}{{ - 60}}$ vì 7.( - 60) = ( - 12).35 = - 420

Cách 2: $\frac{7}{{ - 12}} = \frac{{7.5}}{{\left( { - 12} \right).5}} = \frac{{35}}{{ - 60}}$ $\frac{7}{{ - 12}} = \frac{{7.5}}{{\left( { - 12} \right).5}} = \frac{{35}}{{ - 60}}$

c) Cách 1: $\frac{{ - 8}}{{14}} = \frac{{12}}{{ - 21}}$ $\frac{{ - 8}}{{14}} = \frac{{12}}{{ - 21}}$ vì ( - 8).( - 21) = 14.12 = 168

Cách 2: $\frac{{ - 8}}{{14}} = \frac{{ - 8:2}}{{14:2}} = \frac{{ - 4}}{7} = \frac{{\left( { - 4} \right).\left( { - 3} \right)}}{{7.\left( { - 3} \right)}} = \frac{{12}}{{ - 21}}$ $\frac{{ - 8}}{{14}} = \frac{{ - 8:2}}{{14:2}} = \frac{{ - 4}}{7} = \frac{{\left( { - 4} \right).\left( { - 3} \right)}}{{7.\left( { - 3} \right)}} = \frac{{12}}{{ - 21}}$

Bài 6 trang 12 SBT Toán 6 tập 2

Dùng phân số để viết các đại lượng khối lượng sau theo tạ, theo tấn.

a) 223 kg;

b) 18 kg;

c) 2020 kg;

d) 7 kg.

Đáp án

a) 223 kg = $\frac{{223}}{{100}}$ $\frac{{223}}{{100}}$ tạ = $\frac{{223}}{{1000}}$ $\frac{{223}}{{1000}}$ tấn;

b) 18 kg = $\frac{{18}}{{100}}$ $\frac{{18}}{{100}}$ tạ = $\frac{9}{{50}}$ $\frac{9}{{50}}$ tạ = $\frac{9}{{500}}$ $\frac{9}{{500}}$tấn;

c) 2020 kg = $\frac{{2020}}{{100}}$ $\frac{{2020}}{{100}}$ tạ = $\frac{{101}}{5}$ $\frac{{101}}{5}$ tạ = $\frac{{101}}{{50}}$ $\frac{{101}}{{50}}$ tấn;

d) 7 kg = $\frac{7}{{100}}$ $\frac{7}{{100}}$ tạ = $\frac{7}{{1000}}$ $\frac{7}{{1000}}$ tấn.

Bài 7 trang 12 SBT Toán 6 tập 2

Dùng phân số với mẫu số dương nhỏ nhất để viết các đại lượng dung tích sau theo lít.

a) 600 ml;

b) 280 ml;

c) 1300 ml;

d) 970 ml.

Đáp án

a) 600 ml = $\frac{{600}}{{1000}}l = \frac{6}{{10}}l = \frac{3}{5}l$ $\frac{{600}}{{1000}}l = \frac{6}{{10}}l = \frac{3}{5}l$.;

b) 280 ml = $\frac{{280}}{{1000}}l = \frac{{28}}{{100}}l = \frac{7}{{25}}l$ $\frac{{280}}{{1000}}l = \frac{{28}}{{100}}l = \frac{7}{{25}}l$.;

c) 1300 ml = $\frac{{1300}}{{1000}}l = \frac{{13}}{{10}}l$ $\frac{{1300}}{{1000}}l = \frac{{13}}{{10}}l$.;

d) 970 ml = $\frac{{970}}{{1000}}l = \frac{{97}}{{100}}l$ $\frac{{970}}{{1000}}l = \frac{{97}}{{100}}l$..

Bài 8 trang 12 SBT Toán 6 tập 2

Dùng phân số với mẫu số dương nhỏ nhất để biểu thị phần tô màu trong mỗi hình vẽ sau:

Đáp án

a) Phân số biểu thị phần tô màu là $\frac{{30}}{{40}} = \frac{3}{4}$ $\frac{{30}}{{40}} = \frac{3}{4}$.

b) Phân số biểu thị phần tô màu là $\frac{{25}}{{40}} = \frac{5}{8}$ $\frac{{25}}{{40}} = \frac{5}{8}$.

>> Bài tiếp theo: Giải SBT Toán 6 Bài 3: So sánh phân số

Trên đây là toàn bộ Đáp án Giải SBT Toán 6 Bài 2: Tính chất cơ bản của phân số sách Chân trời sáng tạo để các em học sinh ôn tập củng cố các dạng bài tập hình học, vận dụng giải. Lời giải SGK Toán 6 CTST tương ứng:

Toán lớp 6 bài 2 Tính chất cơ bản của phân số

Các em học sinh tham khảo thêm Toán lớp 6 Cánh Diều và Toán lớp 6 Kết nối tri thức. Đáp án các môn sách mới chương trình GDPT lớp 6 liên tục được VnDoc cập nhật, các bạn cùng theo dõi nhé.

Chia sẻ, đánh giá bài viết