Ba phương pháp tìm giá trị lớn nhất và giá trị nhỏ nhất

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số là dạng toán thường gặp trong các đề thi tốt nghiệp THPT hay các đề thi vào đại học, cao đẳng. Tài liệu "Ba phương pháp tìm giá trị lớn nhất và giá trị nhỏ nhất" giúp các em học sinh nắm được những phương pháp cơ bản để tìm giá trị lớn nhất hay nhỏ nhất của một hàm số hay biểu thức nào đó.

PHƯƠNG PHÁP TÌM GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT

BA PHƯƠNG PHÁP CƠ BẢN

TÌM GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT

CỦA HÀM SỐ, BIỂU THỨC.

A. BÀI TOÁN MỞ ĐẦU:

Tìm giá trị nhỏ nhất (GTNN) của hàm số: y= (x + 1)² + (x – 3)².

Giải . Hàm số viết lại: y = (x² + 2x + 1) + (x² – 6x + 9) = 2x² – 4x + 10 .

Cách 1. (Dùng Bất đẳng thức ) (BĐT).

Ta có y = 2x² – 4x + 10 = 2(x² – 2x + 1) + 8 = 2(x - 1)² + 8 ≥ 8∀x ∈ R.

Đẳng thức xảy ra khi x = 1.Vậy GTNN = 8 khi và chỉ khi x = 1.

Cách 2. (Dùng điều kiện phương trình có nghiệm) (PT).

Gọi y là giá trị hàm số nên phương trình y = 2x² – 4x + 10 có nghiệm (ẩn là x)

Phương trình tương đương 2x² – 4x +10 – y = 0 có nghiệm khi và chỉ khi Δ ≥ 0 ⇔ 4 – 20 + 2y ≥ 0 ⇔ y ≥ 8. Đẳng thức xảy ra khi phương trình có nghiệm kép x = 1.

Do đó GTNN y = 8 khi và chỉ khi x = 1.

Cách 3. (Dùng phương pháp đạo hàm) ( ĐH).

Xét hàm số y = 2x² – 4x + 10 có đạo hàm y’ = 4x - 4 khi y’ = 0 ⇔ x = 1

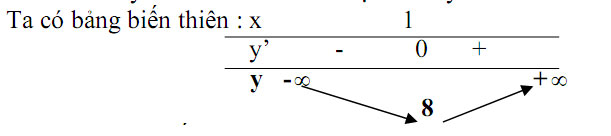
Dựa vào bảng biến thiên ta có GTNN y = 8 khi và chỉ khi x = 1.

B. NỘI DUNG PHƯƠNG PHÁP.

Nội dung bài viết này chỉ nêu lên ba phương pháp cơ bản nhất mà ta thường sử dung để tìm giá trị lớn nhất, giá trị nhỏ nhất của một hàm số hay biểu thức nào đó. Tuỳ theo bài toán cụ thể mà ta có thể sử dụng một trong ba phương pháp trên một cách tối ưu hơn. (Đôi lúc có nhiều bài sử dụng vectơ, phương pháp tọa độ, lượng giác hóa…)

Lưu ý: Khi tìm giá trị lớn nhất , giá trị nhỏ nhất ta luôn chỉ ra trường hợp đẳng thức xảy ra.

Ta hay nhầm lẫn trong trường hợp đánh giá không đúng cho một bất đẳng thức.

Ví dụ trên, nếu không thận trọng ta nói: y= (x + 1)² + (x – 3)² ≥ 0 … thì hỏng rồi!