VnDoc.com

Đạo hàm lớp 12

Tài liệu môn Toán lớp 12

1

I. KiÕn thøc c¬ b¶n.

1. B¶ng ®¹o hµm c¸c hµm sè c¬ b¶n.

Hµm sè

(y = f(x))

§¹o hµm

(y’ = f’(x))

Hµm sè

§¹o hµm

y = c

0

y = tanx

2

1

cos x

y = x

1

y = cotx

2

1

sin x



y = x

n

nx

n-1

y = e

x

e

x

y = 1/x

2

1

x



y = a

x

a

x

. lna

yx

1

2 x

y = lnx

1/x

y = sinx

cosx

y = log

a

x

lna

x

y = cosx

-sinx

2. §¹o hµm cña hµm hîp.

Ta xÐt hµm sè y = f(u(x)). Ta tÝnh ®¹o hµm cña hµm sè ®· cho theo x nh- sau

' ' ' '

.

x x u x

y f f u

B¶ng ®¹o hµm cña hµm sè hîp

Hµm sè

§¹o hµm

Hµm sè

§¹o hµm

y = u

n

n.u

n-1

.u’

y = tanu

2

1

cos u

. u’

y = 1/u

2

1

.'u

u



y = cotu

2

1

sin u



. u’

yu

1

.'

2

u

y = e

u

u’.e

u

y = sinu

u’.cosu

y = a

u

u’.a

u

. lna

y = cosu

- u’.sinu

y = lnu

1

.'u

u

y = log

a

u

ln

.'

a

u

Chó ý:

Khi ¸p dông tÝnh ®¹o hµm cña hµm hîp ta chó ý ban ®Çu tÝnh ®¹o hµm cña hµm sè theo biÕn u

råi nh©n víi ®¹o hµm cña hµm sè u theo biÕn x.

3. C¸c phÐp to¸n ®¹o hµm.

Cho hai hµm sè y = u(x), y = v(x). Khi ®ã

*) (u + v)’ = u’ + v’

*) (u - v)’ = u’ – v’

*) (uv)’ = u’v + v’u

*) (ku)’ = k.u’ ( k lµ h»ng sè)

*)

'

2

''u u v v u

vv











4. §¹o hµm bËc cao cña hµm sè.

2

§¹o hµm bËc n cña hµm sè y = f(x) lµ ®¹o hµm bËc 1 cña ®¹o hµm bËc n – 1 cña hµm sè y =

f(x) ( n > 1).

II. C¸c d¹ng to¸n c¬ b¶n.

1. D¹ng 1. TÝnh ®¹o hµm cña hµm sè.

Ph-¬ng ph¸p. Ta vËn dông c¸c quy t¾c vµ phÐp tÝnh ®¹o hµm, ®Æc biÖt lµ ®¹o hµm cña hµm hîp. NÕu

yªu cÇu tÝnh ®¹o hµm t¹i mét ®iÓm ta cÇn tÝnh ®¹o hµm råi thay vµo ®e ®-îc kÕt qu¶.

VÝ dô 1.

TÝnh ®¹o hµm c¸c hµm sè sau

a)

32

2 3 4y x x x   

b)

sin cos tany x x x  

c)

4

2y x x

d)

cot 3 2y x x  

Gi¶i

a) Ta cã

 

'

3 2 2

' 2 3 4 3 4 3y x x x x x      

b) Ta cã

 

'

2

1

sin cos tan cos sin

cos

y x x x x x

x

     

c) Ta cã

 

'

' 4 3

1

24y x x x

x

   

d) Ta cã

 

'

2

1

cot 3 2 3

sin

y x x

x

     

VÝ dô 2.

TÝnh ®¹o hµm c¸c hµm sè sau t¹i c¸c ®iÓm t-¬ng øng.

a)

32

3 4 1y x x x    

t¹i x

0

= -1.

b)

sin2 cosy x x

t¹i

0

4

x





.

c)

2y x x

t¹i x

0

= 2 .

Gi¶i

a) Ta cã

 

'

' 3 2 2

3 4 1 3 6 4y x x x x x        

suy ra

'

( 1) 3 6 4 13y       

b) Ta cã

 

'

sin2 cos 2cos2 siny x x x x   

suy ra

'

2

2cos sin

4 2 4 2

y

  

     

     

     

     

c) Ta cã

 

'

1

22

2

y x x

x

   

suy ra

 

'

1 1 4 2

22

2 2 2 2

y



  

VÝ dô 3.

TÝnh ®¹o hµm c¸c hµm sè sau

a)

21

2

x

y

x







b)

2

31

1

xx

y

x







c)

42

32y x x  

d)

sin(2 1) cos(1 )y x x   

e)

32yx

f)

2

41y x x  

g)

2

tan( 2 1)y x x  

Gi¶i

a) Ta cã

      

     

''

'

2 2 2

2 1 2 2 1 2

2 1 2 4 2 1 5

2

2 2 2

x x x x

x x x

y

x

x x x

    

   



   







  

b) Ta cã

   

'

2 2 2

'

22

3 1 (2 3)( 1) ( 3 1) 2 4

1

11

x x x x x x x x

y

x

xx



        

  









c) Ta cã

 

'

' 4 2 3

3 2 4 6y x x x x    

d) Ta cã

 

'

sin(2 1) cos(1 ) 2cos(2 1) sin(1 )y x x x x       

3

e) Ta cã

 

'

3

32

2 3 2

yx

x

  



f) Ta cã





'

'2

22

2 4 2

41

2 4 1 4 1

xx

y x x

x x x x



    

   

g) Ta cã

 

'

2

'

'2

22

2 2 2 2

21

tan( 2 1)

cos ( 2 1)

1

2

21

cos ( 2 1) cos ( 2 1)

xx

y x x

xx

x

xx

x

x x x x x



   







   

2. D¹ng 2. Gi¶i ph¬ng tr×nh y’ = 0.

Ph-¬ng ph¸p. Ta tÝnh y’ sau ®ã gi¶i ph¬ng tr×nh y’ = 0.

VÝ dô 1.

Gi¶i ph-¬ng tr×nh y’ = 0 biÕt.

a)

2

1

x

y

x





b)

32

3y x x

c)

32

4 12 9 1y x x x   

d)

2

22

1

xx

y

x







e)

2

33

1

xx

y

x







f)

4

2

5

3

22

x

yx  

g)

42

23y x x   

h)

2

1

xx

y

x







i)

2

1

xx

y

x







Gi¶i

a) Ta có

 

'

22

'

2

1

x x x

y

x













suy ra

 

2

'2

2

0

2

0 0 2 0

2

1

x

xx

y x x

x







      









b) Ta cã

 

'

' 3 2 2

3 3 6y x x x x   

suy ra

'2

0

0 3 6 0

2

x

y x x

x





    







c) Ta cã

 

'

' 3 2 2

4 12 9 1 12 24 9y x x x x x      

Suy ra

'2

3

2

0 12 24 9 0

1

2

x

y x x

x







     









31

,

22

xx

d) Ta cã

 

'

22

'

2

2 2 2

1

x x x x

y

x



  









suy ra

 

2

'2

2

0

2

0 0 2 0

2

1

x

xx

y x x

x







      









e) Ta cã

 

'

22

'

2

3 3 2

1

x x x x

y

x



  









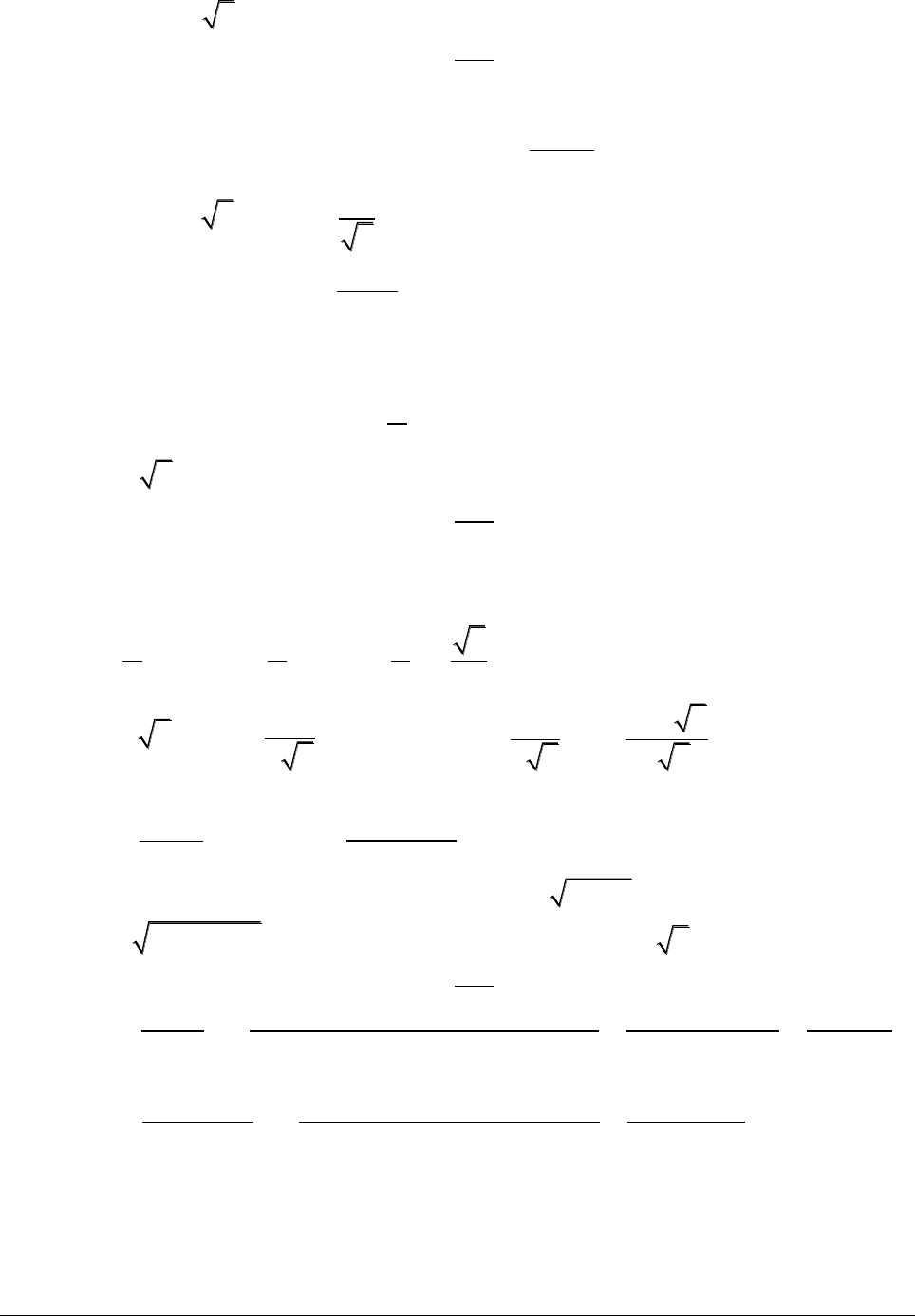
Tổng hợp kiến thức thi THPT Quốc gia môn Toán: Đạo hàm lớp 12

Đạo hàm là một khái niệm cơ bản trong toán học giải tích. Ý nghĩa hình học của khái niệm đạo hàm là ở chỗ nó biểu diễn tốc độ biến thiên của hàm số thông qua hệ số góc của tiếp tuyến với đồ thị biểu diễn hàm số. Về vật lý, đạo hàm biểu diễn vận tốc tức thời của một chất điểm chuyển động với vận tốc không cố định.

CHƯƠNG I: ĐẠO HÀM

I. Kiến thức cơ bản

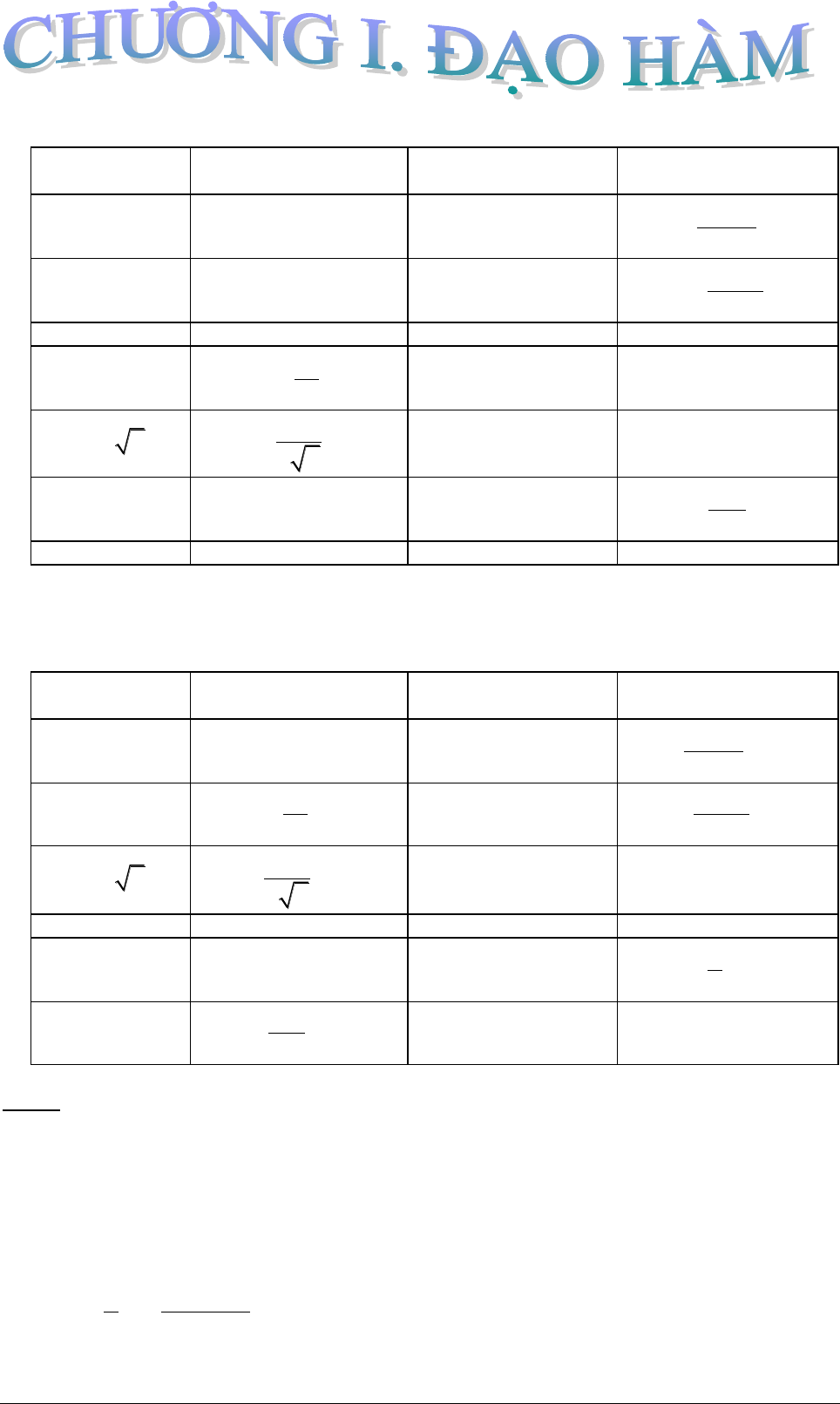
1. Bảng đạo hàm các hàm số cơ bản

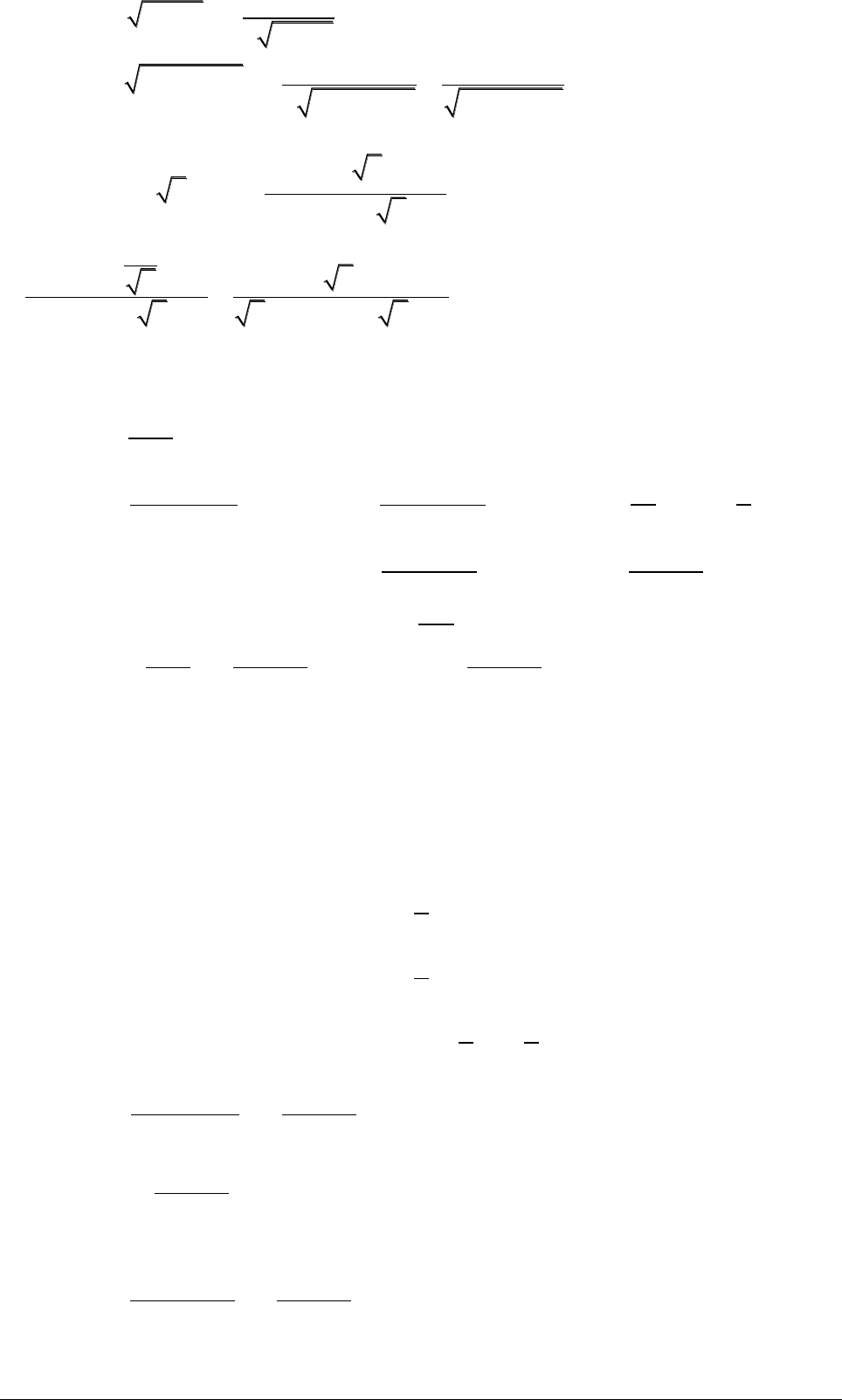
2. Đạo hàm của hàm hợp

Ta xét hàm số y = f(u(x)). Ta tính đạo hàm của hàm số đã cho theo x như sau: y’ₓ = f’ₓ = f’ᵤ.u’ₓ

Bảng đạo hàm của hàm số hợp

Tài liệu môn Toán lớp 12: Đạo hàm

Chú ý: Khí áp dụng tính đạo hàm của hàm số hợp ta chú ý ban đầu tính đạo hàm của hàm số theo biến u rồi nhân với đạo hàm của hàm số u theo biến x.

Đạo hàm là một phận thường xuyên gặp trong các đề thi tốt nghiêp thpt, đề thi tuyển sinh vào các trường đại học, cao đẳng. Để giúp các bạn học sinh hệ thống lại kiến thức phần này, VnDoc.com xin giới thiệu tài liệu đạo hàm lớp 12. Tài liệu này đưa ra những kiến thức cơ bản về đạo hàm, tiếp tuyến của đồ thị hàm số, các bài toán tính tổng…

Hi vọng qua bài viết này bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán lớp 12. Mời các bạn cùng tham khảo thêm tài liệu học tập các môn Ngữ văn lớp 12, Tiếng Anh lớp 12...