Các bài toán giải bằng phương pháp tính ngược từ cuối
Các bài toán giải bằng phương pháp tính ngược
Bài toán tính ngược từ cuối là một dạng toán khó trong chương trình tiểu học. Nhằm giúp các em học sinh học tốt dạng toán này, VnDoc.com xin giới thiệu các bài toán giải bằng phương pháp tính ngược từ cuối. Tài liệu này đưa ra các ví dụ cụ thể và phương pháp làm bài toán tính ngược. Mời các bạn cùng tham khảo.
PHƯƠNG PHÁP TÍNH NGƯỢC TỪ CUỐI
Có một số bài toán cho biết kết quả sau khi thực hiện liên tiếp một số phép tính đối với số phải tìm. Khi giải các bài toán dạng này, ta thường dùng phương pháp tính ngược từ cuối (đôi khi còn gọi là phương pháp suy ngược từ cuối)
Khi giải toán bằng phương pháp tính ngược từ cuối, ta thực hiện liên tiếp các phép tính ngược với các phép tính đã cho trong đề bài. Kết quả tìm được trong bước trước chính là thành phần đã biết của phép tính liền sau đó. Sau khi thực hiện hết dãy các phép tính ngược với các phép tính đã cho trong đề bài, ta nhận được kết quả cần tìm.
Những bài toán giải được bằng phương pháp tính ngược từ cuối thường cũng giải được bằng phương pháp đại số hoặc phương pháp ứng dụng đồ thị (xem các số tiếp theo).
Ví dụ 1: Tìm một số, biết rằng tăng số đó gấp đôi, sau đó cộng với 16 rồi bớt đi 4 và cuối cùng chia cho 3 ta được kết quả bằng 12.
Phân tích: Trong bài này ta đã thực hiện liên tiếp đối với dãy số cần tìm dãy các phép tính dưới đây:
x 2, + 16, - 4, : 3 cho kết quả cuối cùng bằng 12.
- Ta có thể xác định được số trước khi chia cho 3 được kết quả là 12 (Tìm số bị chia khi biết số chia và thương số).
- Dựa vào kết quả tìm được ở bước 1, ta tìm được số trước khi bớt đi 4 (Tìm số bị trừ khi biết số trừ và hiệu số).
- Dựa vào kết quả tìm được ở bước 2, ta tìm được số trước khi cộng với 16 (Tìm số hạng chưa biết khi biết số hạng kia và tổng số).
- Dựa vào kết quả tìm được ở bước 3, ta tìm được số trước khi nhân với 2, chính là số cần tìm (Tìm thừa số chưa biết khi biết tích và thừa số kia).
Từ phân tích trên ta đi đến lời giải như sau:
Số trước khi chia cho 3 là:
12 x 3 = 36
Số trước khi bớt đi 4 là:
36 + 4 = 40
Số trước khi cộng với 16 là:
40 - 16 = 24
Số cần tìm là:
24 : 2 = 12
Trả lời: Số cần tìm là 12.
Ví dụ 2: Tìm ba số, biết rằng sau khi chuyển 14 đơn vị từ số thứ nhất sang số thứ hai, chuyển 28 đơn vị từ số thứ hai sang số thứ ba rồi chuyển 7 đơn vị từ số thứ ba sang số thứ nhất ta được ba số đều bằng 45.
Phân tích: Ta có thể minh họa các thao tác trong đề bài bằng sơ đồ sau:
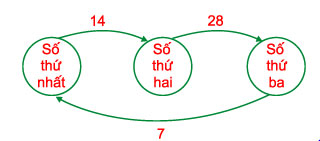
Ta có:
Số thứ nhất: - 14; + 7 cho kết quả là 45
Số thứ hai: + 14; - 28 cho kết quả là 45
Số thứ ba: + 28; - 7 cho kết quả là 45
Từ phân tích trên ta đi đến lời giải của bài toán như sau:
Số thứ nhất là: 45 - 7 + 14 = 52.
Số thứ hai là: 45 + 28 - 14 = 49.
Số thứ ba là: 45 + 7 - 28 = 24.
Trả lời: Ba số cần tìm là: 52; 49 và 24.


