Chuyên đề - Dãy số viết theo quy luật
Dãy số viết theo quy luật Toán lớp 6
Chuyên đề - Dãy số viết theo quy luật là tài liệu bôi dưỡng học sinh giỏi Toán 6 theo chuyên đề. Tài liệu này đưa ra các phương pháp giải bài toán dãy số viết theo quy luật, có kèm theo các ví dụ cụ thể và các bài tự luyện, giúp các em củng cố và nâng cao kiến thức hiệu quả. Chúc các em học tốt.
CHUYÊN ĐỀ TOÁN 6 (BD HSG)
DÃY SỐ VIẾT THEO QUI LUẬT
I. Phương pháp dự đoán và quy nạp:
Trong một số trường hợp khi gặp bài toán tính tổng hữu hạn
Sn = a1 + a2 + .... an (1)
Bằng cách nào đó ta biết được kết quả (dự đoán, hoặc bài toán chứng minh khi đã cho biết kết quả). Thì ta nên sử dụng phương pháp này và hầu như thế nào cũng chứng minh được.
Ví dụ 1: Tính tổng Sn = 1 + 3 + 5 +... + (2n -1)
Thử trực tiếp ta thấy: S1 = 1
S2 = 1 + 3 = 22
S3 = 1+ 3 + 5 = 9 = 32
... ... ...
Ta dự đoán Sn = n2
Với n = 1; 2; 3 ta thấy kết quả đúng
Giả sử với n = k (k ≥ 1) ta có Sk = k2 (2)
Ta cần phải chứng minh Sk + 1 = (k +1)2 (3)
Thật vậy cộng 2 vế của (2) với 2k +1 ta có
1 + 3 + 5 +... + (2k – 1) + ( 2k +1) = k2 + (2k +1)
Vì k2 + (2k +1) = (k +1)2 nên ta có (3) tức là Sk+1 = ( k +1)2
Theo nguyên lý quy nạp bài toán được chứng minh
Vậy Sn = 1 + 3 + 5 + ... + (2n -1) = n2
Tương tự ta có thể chứng minh các kết quả sau đây bằng phương pháp quy nạp toán học.
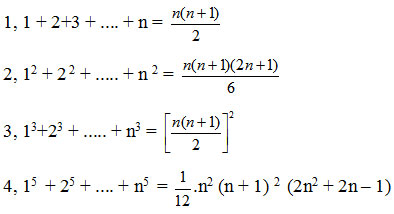
II. Phương pháp khử liên tiếp:
Giả sử ta cần tính tổng (1) mà ta có thể biểu diễn ai, i = 1, 2, 3..., n, qua hiệu hai số hạng liên tiếp của 1 dãy số khác, chính xác hơn, giả sử:
a1 = b1 - b2
a2 = b2 - b3
.... .... .....
an = bn – bn+ 1
Khi đó ta có ngay:
Sn = (b1 – b2) + (b2 – b3) + ...... + (bn – bn + 1) = b1 – bn + 1
Ví dụ 2: Tính tổng:
![]()
Ta có:
![]()
Do đó:
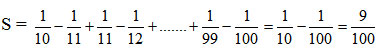
Dạng tổng quát: