Công thức tính lãi kép

Bài viết dưới đây cung cấp công thức tính lãi đơn, tính lãi kép đầy đủ, rõ ràng và dễ hiểu, kèm theo ví dụ minh họa giúp học sinh nắm chắc cách tính toán và vận dụng linh hoạt vào các dạng bài tập. Đây là tài liệu hữu ích hỗ trợ các em ôn luyện hiệu quả cho kỳ thi tốt nghiệp THPT và các kỳ kiểm tra quan trọng.

Lãi đơn

1. Lãi đơn là gì

Số tiền lãi chỉ tính trên số tiền gốc mà không tính trên số tiền lãi do số tiền gốc sinh ra. Tức là tiền lãi của kì hạn trước không được tính vào vốn để tính lãi cho kì hạn kế tiếp.

2. Công thức tính lãi đơn

Công thức tính lãi đơn:

T = M (1 + r x n)

Trong đó:

• T: Số tiền cả vốn lẫn lãi sau n kỳ hạn;
• M: Tiền gửi ban đầu;
• n: Số kỳ hạn tính lãi;
• r: Lãi suất định kỳ, tính theo %.

3. Bài toán tính lãi đơn

Ví dụ1. Bác An gửi vào ngân hàng 20 triệu với lãi đơn là 5%/năm. Hỏi sau 7 năm, bác An nhận được cả vốn lẫn lãi là bao nhiêu?

Lời giải:

Áp dụng công thức với A = 20 triệu; r = 5% và n = 7 ta được

Số tiền bác An nhận được sau 7 năm là: S7 = 20.(1 + 7,5%) = 27 triệu.

Ví dụ 2. Anh Bình gửi tiết kiệm 10 triệu đồng với lãi đơn là 1,5%/ quý. Hỏi sau ít nhất bao lâu thì anh Bình rút được cả gốc lẫn lãi là 12 triệu đồng. Biết ngân hàng chỉ chả tiền khi hết kì hạn.

Lời giải:

Gọi n là số kì hạn

Vậy sau ít nhất 14 quý (48 tháng) thì anh Bình rút được 12 triệu.

Lãi kép

1. Lãi kép là gì?

Là thể thức mà hết kì hạn này, tiền lãi được nhập vào vốn của kì tiếp theo.

Ví dụ 1. Anh Tâm gửi tiết kiệm 50 triệu với lãi kép 5%/năm. Sau 10 năm anh ra ngân hàng rút cả gốc lẫn lãi về để đầu tư làm ăn. Hỏi số tiền anh rút về là bao nhiêu?

Lời giải:

Áp dụng công thức tính lãi kép với M = 50; r = 5%; n = 10 ta được:

Số tiền anh Tâm rút về là: S₁₀ = 50(1 + 5%)¹⁰ ≈ 81,44 triệu đồng.

2. Công thức tính lãi kép

a. Lãi kép, gửi một lần

T = M (1 + r)ⁿ

Trong đó:

• T: Số tiền cả vốn lẫn lãi sau n kỳ hạn;
• M: Tiền gửi ban đầu;
• n: Số kỳ hạn tính lãi;
• r: Lãi suất định kỳ, tính theo %.

b. Lãi kép, gửi định kỳ

Trường hợp 1: Tiền được gửi vào cuối mỗi tháng

Cuối tháng thứ nhất cũng là lúc người đó bắt đầu gửi tiền:

𝑇₁ = 𝑀

Cuối tháng thứ 2, người đó có số tiền là:

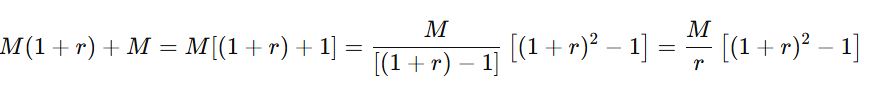
Cuối tháng thứ 3:

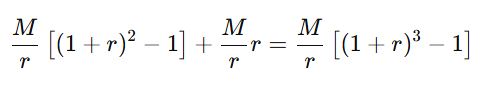
Cuối tháng thứ n, người đó có số tiền là:

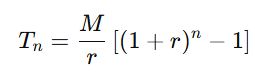
Tiếp cận khác về công thức:

Tiền gửi tháng thứ nhất sau n-1 kỳ hạn n – 1 tháng thành: M(1+r)^n-1

Tiền gửi tháng thứ nhất sau n-2 kỳ hạn n – 2 tháng thành: M(1+r)^n-2

Tiền gửi tháng cuối cùng là: M(1+r)⁰

Vậy áp dụng công thức tổng cấp số nhân, số tiền cuối tháng n là:

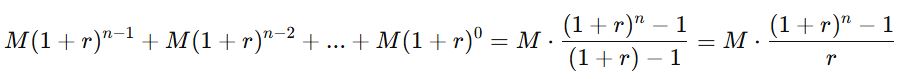
Ta cũng được công thức trên:

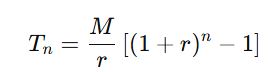
Trường hợp 2: Tiền gửi vào đầu mỗi tháng

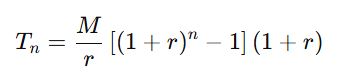
3. Bài toán tính lãi kép

Bài 1: Anh Tâm gửi tiết kiệm 50 triệu với lãi kép 5%/năm. Sau 10 năm anh ra ngân hàng rút cả gốc lẫn lãi về để đầu tư làm ăn. Hỏi số tiền anh rút về là bao nhiêu?

Lời giải:

Áp dụng công thức tính lãi kép với M = 50; r = 5%; n = 10 ta được:

Số tiền anh Tâm rút về là: S₁₀ = 50(1 + 5%)¹⁰ ≈ 81,44 triệu đồng.

Bài 2: Con trai ông Phú đang học lớp 6. Ông Phú quyết định gửi một số tiền tiết kiệm để mua chiếc xe máy tặng con làm quà khi đỗ lớp 10. Biết rằng chiếc xe máy trị giá 17 triệu và lãi suất năm là 6,05%. Hỏi ông Phú cần gửi bao nhiêu tiền để sau 4 năm có đủ tiền mua xe tặng con?

Giải:

Gọi số tiền ông Phú cần gửi là A

Số tiền cả gốc lẫn lãi sau 4 năm ông có là: S₄ = A(1 + 6,05)⁴

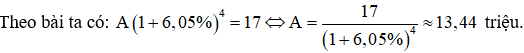
Bài 3: Đều mỗi tháng chú Ba đều gửi vào ngân hàng 500 nghìn đồng với lãi suất 0,6%/ tháng. Sau 1 năm thì số tiền chú Ba nhận được cả gốc lẫn lãi là bao nhiêu sau khi ngân hàng đã tính lãi tháng cuối cùng?

Lời giải:

Áp dụng công thức trên với: triệu; r = 0.6% và tháng ta được:

Số tiền chú Ba nhận được là: 

Bài 4: 

Hết vụ vải, tổng kết anh P được 200 triệu đồng. Anh dự định gửi ngân hàng với lãi suất 0,7%/tháng. Cuối mỗi tháng anh rút ra 6 triệu để tiêu. Hỏi:

a. Sau 2 năm thì anh P còn lại bao nhiêu tiền

b. Tính xem bao giờ thì anh P rút được nhiều nhất bao nhiêu tháng.

Giải: 

a. Áp dụng công thức tính lãi suất với A = 200 triệu; a = 6 triệu và r = 0,7% .

Số tiền anh P còn lại sau 24 tháng là:

b. Số tiền anh P còn lại sau tháng n là:

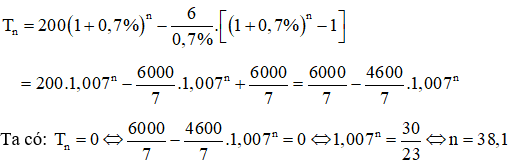
 Do đó anh P rút được nhiều nhất là 38 tháng.