Đề chọn học sinh giỏi Toán THCS năm 2024 – 2025 sở GD&ĐT Hải Phòng
Đề chọn học sinh giỏi Toán THCS
Lớp:
Lớp 9
Môn:
Toán
Dạng tài liệu:
Đề thi HSG
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
Trang 1/4 - Mã đề thi 101
ĐỀ CHÍNH THỨC
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HẢI PHÒNG
(Đề thi gồm 22 câu; 04 trang)
KỲ THI
CHỌN HỌC SINH GIỎI THÀNH PHỐ CẤP THCS
NĂM HỌC 2024 – 2025
ĐỀ THI MÔN: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian phát đề).
Ngày thi: 15/01/2025
Họ và tên thí sinh:................................................................. Số báo danh:.................
Mã đề thi 101
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí
sinh chỉ chọn một phương án.
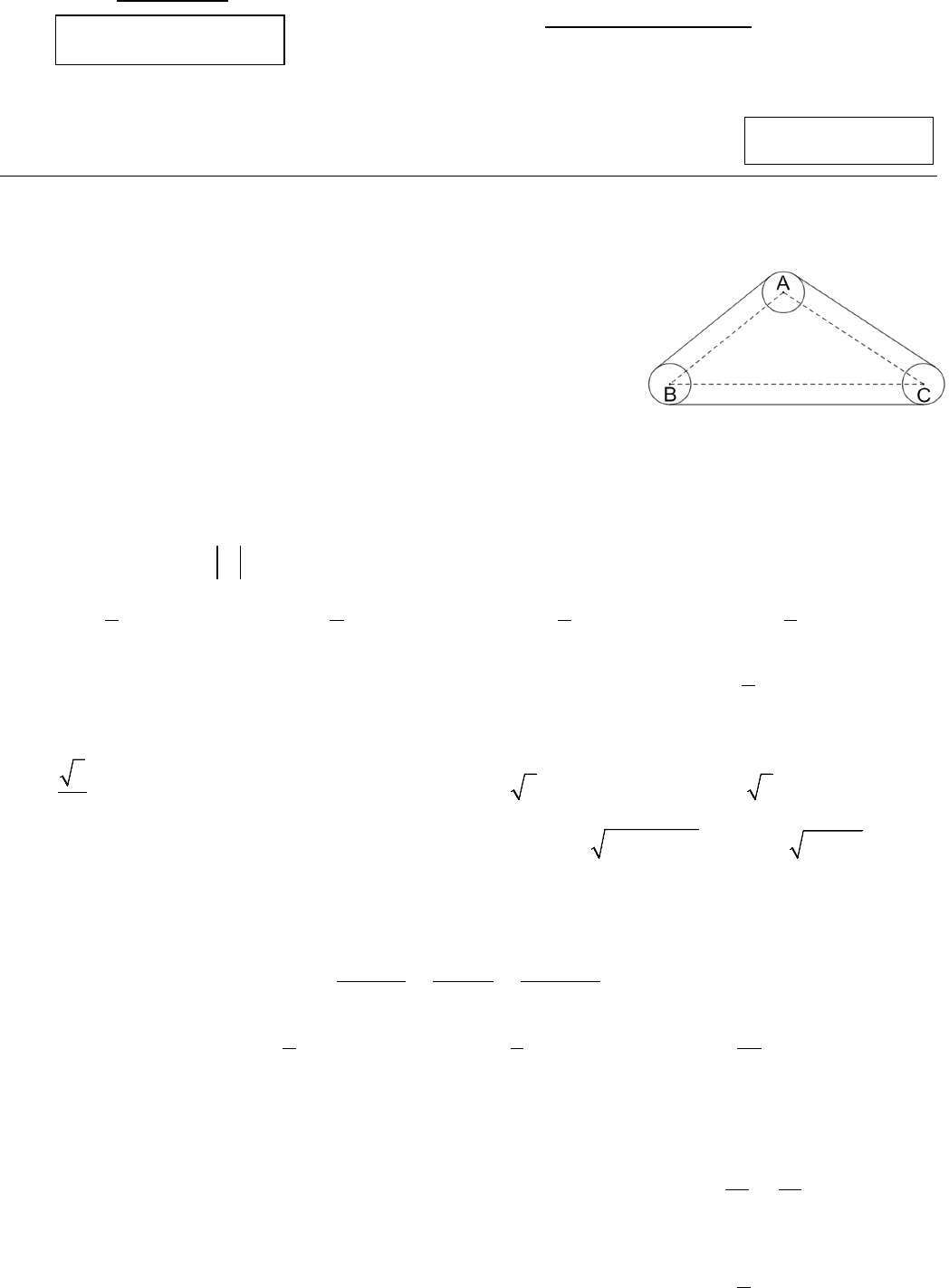
Câu 1: Cho ba bánh xe hình tròn có tâm lần lượt là
,,ABC
có cùng bán
kính bằng
1.
dm
Ba bánh xe đó được nối với nhau bởi một dây cua – roa
không giãn, quay không trượt, được căng như hình vẽ.
Biết
7 ; 8 ; 12 .AB dm AC dm BC dm
Chiều dài của dây cua – roa
xấp xỉ là: (Kết quả làm tròn đến hàng phần mười, lấy
3, 14).
A.
30, 1 .dm
B.
31, 1 .dm
C.
33, 3 .dm
D.
34, 3 .dm
Câu 2: Cho hệ phương trình
25
4
xy
mx y
(
m
là tham số). Để hệ phương trình có nghiệm duy nhất
00
;xy
thỏa mãn
00
xy
thì giá trị của
m
là:
A.
4
.
5
m
B.
7
.
5
m
C.
5
.
7
m
D.
1
.
5
m
Câu 3: Cho
ABC
nhọn, có ba đường cao
,,AD BI CK
cắt nhau tại
.H
Nếu
1
4
HD AD
thì giá trị của biểu
thức
tan .tanABC ACB
là:
A.
2
.
2
B.
4.
C.
2.
D.
2 2.
Câu 4: Tổng các nghiệm của phương trình
32 2
2 612 1 131x x x xx x x
là:
A.
1.
B.
0.
C.
2.
D.
1.
Câu 5: Cho các số thực dương
,ab
và
c
thỏa mãn
2
2 4.acbc c
Giá trị lớn nhất của biểu thức
22
23 3 2
a b ab
P
b c a c bc ca
là:
A.
1.
B.
3
.
2
C.
5
.
2
D.
41
.
30
Câu 6: Cho hình chữ nhật
ABCD
có
3 9 ( 0).AB AD a a
Đường thẳng vuông góc với
AC
tại
C
cắt
đường thẳng
AB
tại
.E
Lấy điểm
M
trên cạnh
( , ).
ABMAMB
Các đường thẳng
CM
và
AD
cắt nhau
tại
.N
Gọi
1
S
là diện tích của
CME
và
2
S
là diện tích của
.AMN
Nếu
1
2
15
8
S
S
thì độ dài đoạn
thẳng
AM
là:
A.
.a
B.
2.a
C.
4.a
D.
3
.
2
a
Trang 2/4 - Mã đề thi 101
Câu 7: Cho
,xy
là các số nguyên thỏa mãn
2
2 7 0.x xy y x
Tổng tất cả các giá trị của
x
là:
A.
4.
B.
0.
C.
8.
D.
6.
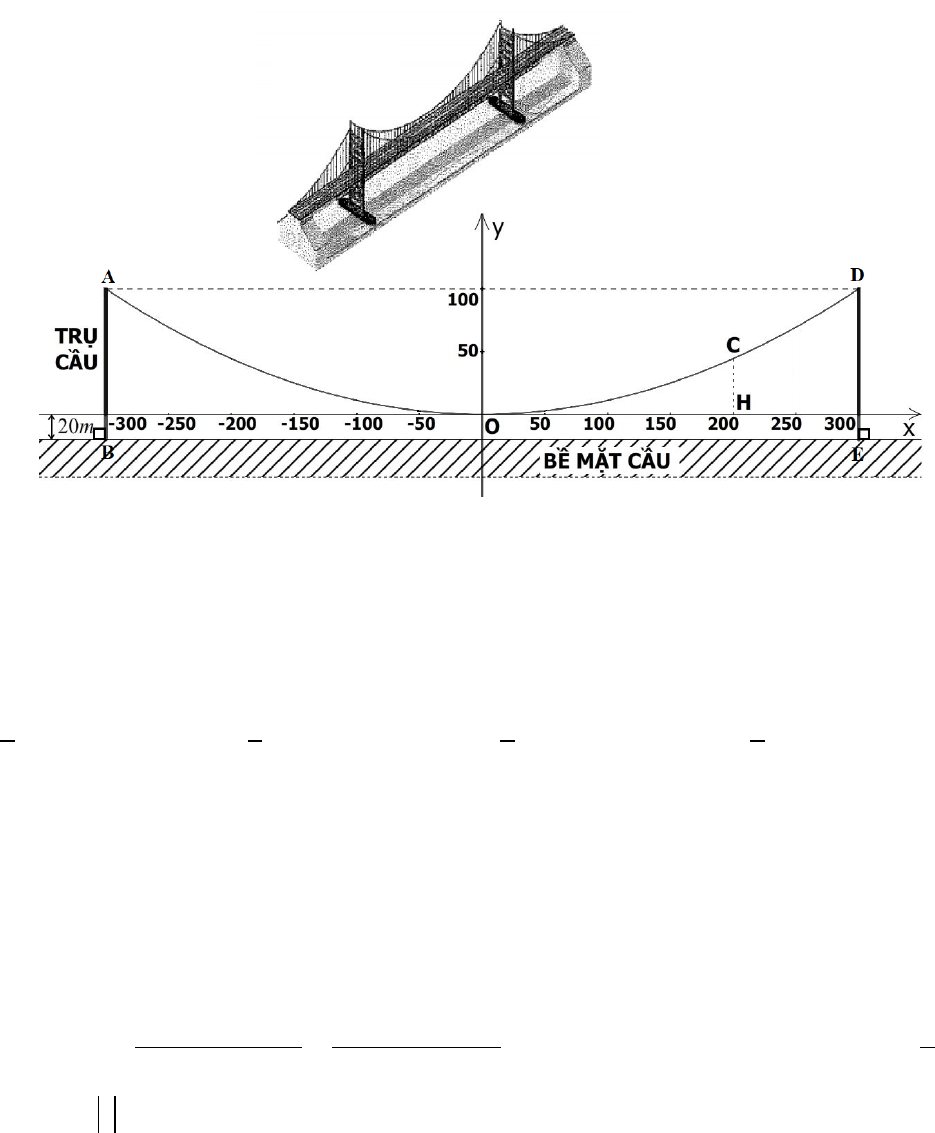
Câu 8: Giả sử một dây cáp của một cây cầu treo có dạng Parabol
2
:0
P y ax a
trong hệ trục tọa độ
Oxy
như hình vẽ. Ở đó
Ox
song song với bề mặt của cây cầu. Biết rằng, hai điểm cao nhất của dây cáp cách
nhau
600
m
và đều cách bề mặt của cây cầu
120 .m
Điểm thấp nhất
O
của dây cáp cách bề mặt của cây cầu
20 .m
Nếu
C
là một điểm nằm trên dây cáp,
H
là hình chiếu của
C
trên trục
,Ox
200
OH m
thì độ
dài
CH
xấp xỉ là:
(Giả sử bề mặt của cây cầu là bằng phẳng, kết quả làm tròn đến hàng phần mười).
A.
44, 4 .
m
B.
64, 9 .m
C.
44, 5 .m
D.
69, 4 .m
Câu 9: Cho biểu thức
2026 2024
1,An n
có bao nhiêu số tự nhiên
n
để giá trị của
A
là số nguyên tố?
A.
1.
B.
3.
C.
2.
D.
4.
Câu 10: Gieo một đồng xu cân đối, đồng chất ba lần liên tiếp và quan sát sự xuất hiện của mặt sấp và mặt
ngửa. Xác suất của biến cố: “Mặt ngửa xuất hiện ít nhất hai lần” là:
A.
3
.
4
B.
1
.
2
C.
1
.
4
D.
7
.
8
Câu 11: Trên một mảnh đất hình chữ nhật
ABCD
có diện tích
2
250 ,
m
người chủ dùng một phần đất hình
chữ nhật
( )
∈∈∈;;AEHK E AB H BD K AD
để trồng hoa. Nếu phần đất trồng hoa
AEHK
có diện tích lớn
nhất thì số tiền cần chi trả cho việc trồng hoa là bao nhiêu? Biết chi phí trồng hoa là
50000
đồng
2
/.m
A.
5000000
đồng. B.
3125000
đồng. C.
2500000
đồng. D.
3750000
đồng.
Câu 12: Cho phương trình
2
6 2 0,x mx m
(
x
là ẩn,
m
là tham số) có hai nghiệm phân biệt
12
;xx
.
Biểu thức
2
2
12
22
21
66
66 4
x mx m
m
A
x mx m m
đạt giá trị nhỏ nhất khi
a
m
b
với
*
, ,, 1a b ab
. Tổng
ab
là:
A.
1.ab
B.
13.ab
C.
3.ab
D.
21.ab
Trang 3/4 - Mã đề thi 101
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi
câu, thí sinh chọn đúng hoặc sai.
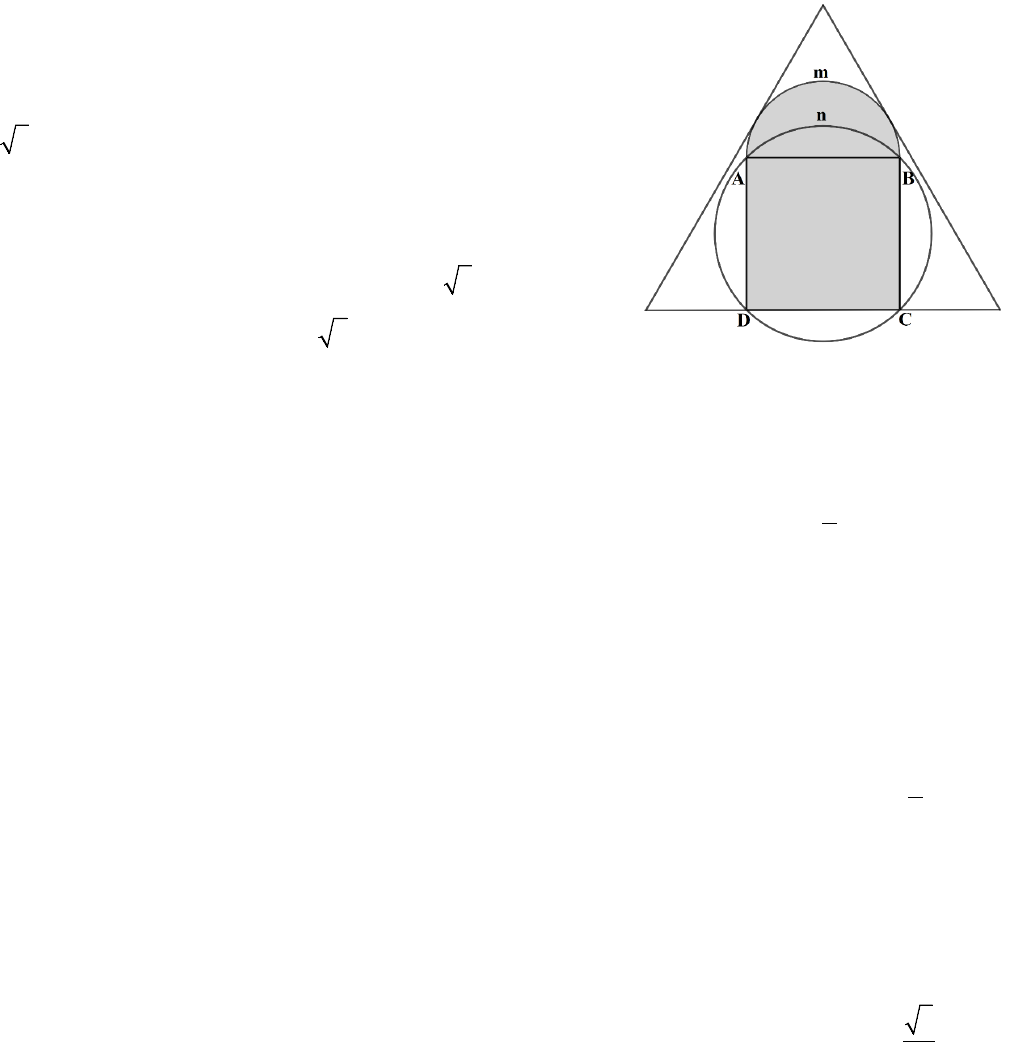
Câu 1: Cho hình vuông
,
ABCD
trên cùng một nửa mặt phẳng bờ
AB
không chứa
,
CD
vẽ nửa hình tròn đường kính
.AB
Dựng tam
giác đều có hai cạnh tiếp xúc với nửa hình tròn trên, cạnh còn lại chứa
đoạn thẳng
CD
(như hình vẽ). Cho độ dài mỗi cạnh của tam giác đều
là
45 ,cm
lấy
3,14.
a) Vẽ đường tròn ngoại tiếp hình vuông
.ABCD
Diện tích hình
được giới hạn bởi cung
AmB
và cung
AnB
là
2
3, 75 .cm
b) Độ dài mỗi cạnh của hình vuông
ABCD
là
25 .cm
c) Diện tích của tam giác đều là
2
20 3 .cm
d) Diện tích phần được tô đậm trên hình vẽ xấp xỉ là
2
20, 9 .cm
(Kết quả làm tròn đến hàng phần mười).
Câu 2: Trong một hộp kín có
6
viên bi màu đỏ,
4
viên bi màu xanh và
8
viên bi màu vàng có kích thước và
khối lượng như nhau.
a) Chọn ngẫu nhiên
1
viên bi trong hộp đó. Xác suất chọn được
1
viên bi màu xanh là
2
.
9
b) Thêm vào hộp đó
a
viên bi màu đỏ,
b
viên bi màu xanh và
c
viên bi màu vàng (có cùng kích thước và
khối lượng với các viên bi đã có trong hộp;
*
,, )abc
sao cho xác suất chọn được trong hộp lúc này một
viên bi mỗi màu: đỏ, xanh và vàng đều không đổi so với ban đầu. Giá trị nhỏ nhất của tổng
abc
là
18.
c) Chọn ngẫu nhiên
7
viên bi trong hộp đó. Có
2
kết quả thuận lợi cho biến cố: “Trong
7
viên bi được
chọn có số lượng viên bi màu đỏ bằng số lượng viên bi màu vàng”.
d) Thêm vào hộp đó
x
viên bi màu trắng
*
()x
có cùng kích thước và khối lượng với các viên bi trong
hộp, sau đó chọn ngẫu nhiên
1
viên bi trong hộp. Nếu xác suất chọn được
1
viên bi màu trắng là
1
3
thì
x
là
số lẻ.
Câu 3: Cho
,AB
là hai điểm cố định và
8,AB cm
M
là một điểm di động trên đoạn thẳng
,.
ABMAMB
Trên cùng một nửa mặt phẳng bờ
,AB
vẽ hai hình vuông
AMCD
và
.BMEF
Gọi
N
và
P
lần lượt là giao điểm của các cặp đường thẳng
AE
và
;BC AC
và
.BE
a) Gọi
O
là trung điểm của đoạn thẳng
.AB
Nếu
CO
là tia phân giác của
ACM
thì
2
1.
2
MB cm
b) Các điểm
, ,,AN P B
cùng thuộc một đường tròn.
c)
2
..MN ND DF
d) Độ dài lớn nhất của đoạn thẳng
MN
là
4.cm
Câu 4: Cho
*
;,m pq
là hai số nguyên tố thỏa mãn:
25
.
21.1
m
pq
a) Có hai bộ số
,,mpq
thỏa mãn
1.
b) Ta luôn có
432
1.qqqq p
c) Khi
2p
có duy nhất cặp số
00
;mq
thỏa mãn
1.
d)
q
luôn là số lẻ.
Đề chọn học sinh giỏi Toán THCS năm 2024 – 2025 sở GD&ĐT Hải Phòng được thiết kế bám sát chương trình, giúp học sinh phát triển tư duy và kỹ năng giải toán nâng cao.
Với nội dung được chọn lọc kỹ lưỡng, bài viết không chỉ giúp giáo viên hiểu rõ cấu trúc đề, ra đề sát với chuẩn năng lực mà còn là nguồn tài liệu hữu ích để nâng cao hiệu suất ôn thi cho học trò.



