Đề thi học kì 2 môn Toán lớp 8 trường THCS Quang Huy, Phù Yên năm 2015 - 2016
Đề thi học kì 2 môn Toán lớp 8
Đề thi học kì 2 môn Toán lớp 8 trường THCS Quang Huy, Phù Yên năm 2015 - 2016 là đề thi học kì 2 lớp 8 môn Toán có đáp án. VnDoc xin giới thiệu tới các bạn tài liệu này giúp các bạn ôn thi học kì II môn toán lớp 8 tốt hơn, đạt điểm cao trong bài thi của mình. Mời các bạn tham khảo.
Đề thi học kì 2 môn Hóa học lớp 8 trường PTDTBT THCS Trà Thọ, Tây Trà năm 2015 - 2016
Đề thi học kì 2 môn Sinh học lớp 8 trường THCS số 2 Trà Phong, Tây Trà năm 2013 - 2014
Đề thi học kì 2 môn Ngữ văn lớp 8 trường THCS Quỹ Nhất, Nam Định năm 2015 - 2016
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO PHÙ YÊN
TRƯỜNG THCS QUANG HUY
ĐỀ KIỂM TRA HỌC KÌ II
Năm: 2015 - 2016
MÔN: TOÁN – LỚP 8
(Thời gian làm bài 90 phút)
Câu 1: (2 điểm)
a) Bậc của đơn thức là gì?
b) Tìm bậc của đơn thức: 7x2y5z7, -3/4xy4
Câu 2: (2 điểm)
a) Phát biểu tính chất về ba đường trung trực
b) Phát biểu tính chất ba đường phân giác của tam giác.
Câu 3: (1điểm) Thu gọn các đơn thức, đa thức sau:
a) 3x2y . (-2xy3z)
b) 5a2b + 6a3b2 – 12a2b + 4a3b2
Câu 4: (1 điểm). Phát biểu định lí quan hệ giữa đường vuông góc và đường xiên.
Câu 5: (1 điểm). Năng suất lúa đông xuân (tính theo tạ/ha) của 20 hợp tác xã được ghi lại trong bảng sau:
| 45 | 45 | 40 | 40 | 35 | 40 | 30 | 45 | 35 | 40 |
| 40 | 40 | 35 | 45 | 45 | 35 | 45 | 40 | 30 | 40 |
a) Lập bảng "tần số"
b) Tính số trung bình cộng
c) Tìm Mốt của dấu hiệu
Câu 6: (1 điểm)
a) Tính giá trị của đa thức P(x) = 5x2 – 4x – 4, tại x = – 2
b) Cho các đa thức:
A(x) = x3 + 3x2 – 4x – 12
B(x) = 2x3 – 3x2 + 4x + 1
Tính A(x) + B(x)
Câu 7: (2 điểm) Cho ΔABC vuông tại B, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm E sao cho ME = MA Chứng minh rằng:
a) ΔABM = ΔECM
b) AC > CE.
c) ∠BAM > ∠MAC
Đáp án đề thi học kì 2 môn Toán lớp 8
Câu 1.
a) Bậc của đơn thức có hệ số khác 0 là tổng số mũ của tất cả các biến có trong đơn thức đó. (1 điểm)
b) 7x2y5z7 có bậc 14 (0,5 điểm)
-3/4xy4 có bậc 5 (0,5 điểm)
Câu 2.
Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác (1 điểm)
Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác. (1 điểm)
Câu 3.
a) 3x2y . (- 2xy3z) = – 6x3y4z (0,5 điểm)
b) 5a2b + 6a3b2 – 12a2b + 4a3b2 = 10 a3b2 – 7 a2b (0,5 điểm)
Câu 4. Trong các đường xiên và đường vuông góc kẻ từ môt điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất. (1 điểm)
Câu 5.
a) Bảng tần số (0,25 điểm)
| Giá trị (x) | 30 | 35 | 40 | 45 | |
| Tần số (n) | 2 | 5 | 7 | 6 | N = 20 |
b) Số trung bình cộng của dấu hiệu (0,5 điểm)
![]()
c) Mốt của dấu hiệu M0 = 40 (0,25 điểm)
Câu 6.
a) Ta có P(-2) = 5 .(-2)2 – 4.(-2) – 4
= 5. 4 + 8 – 4 = 20 + 8 – 4 = 24
Vậy giá trị của đa thức P(x) = 5x2 – 4x – 4 tại x = -2 là 24 (0,5đ)
b) A(x) + B(x) = (x3 + 3x2 – 4x – 12) + (2x3 – 3x2 + 4x + 1)
= x3 + 3x2 – 4x – 12 + 2x3 – 3x2 + 4x + 1
= 3x3 – 11 (0,5đ)
Câu 7.
Vẽ hình, ghi Gt-Kl (0,5 điểm)
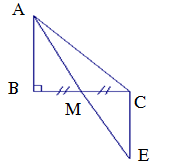
a) Xét Δ ABM và Δ ECM
Có: AM = ME (gt)
∠AMB = ∠AME (đối đỉnh)
MB = MC (gt) (0,25 điểm)
=> Δ ABM = Δ ECM (c-g-c) (0,25 điểm)
b) Ta có Δ ABM vuông tại B, nên AC là cạnh lớn nhất
Suy ra: AC > AB
Mà AB = CE (vì Δ ABM = Δ ECM)
Do đó AC > CE (0,5 điểm)
c) Vì AC > CE nên ∠MEC > ∠MAC
mà ∠MAB = ∠MEC (vì Δ ABM = Δ ECM)
Suy ra: ∠MAB > ∠MAC (0,5 điểm)
(Học sinh có cách giải khác, đúng vẫn được điểm)



