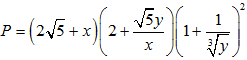Đề thi học sinh giỏi giải toán trên máy tính cầm tay năm học 2012 - 2013 môn Toán khối 12

SỞ GIÁO DỤC VÀ ĐÀO TẠO LONG AN (Đề thi chính thức)

KỲ THI CHỌN HSG GIẢI TOÁN TRÊN MÁY TÍNH CẦM TAY NĂM HỌC 2012-2013 MÔN: TOÁN - KHỐI 12 (Thời gian làm bài 90 phút không kể thời gian giao đề) Ngày thi: 27/01/2013

Chú ý:

- Các giá trị phải tính ra số thập phân, lấy chính xác 5 chữ số thập phân không làm tròn.

- Thí sinh phải ghi tóm tắt cách giải hay công thức tính.

- Đề thi có 10 bài, mỗi bài 1 điểm.

Bài 1.

Cho hàm số . Tính gần đúng tọa độ điểm M thuộc đồ thị (C) sao cho tiếp tuyến của (C) tại điểm M cắt hai trục tọa độ Ox, Oy lần lượt tại A, B và OB = 2OA.

Bài 2.

Tính gần đúng giá trị lớn nhất và giá trị nhỏ nhất của hàm số:

Bài 3.

Tính gần đúng các nghiệm của phương trình:

Bài 4.

Tính gần đúng các nghiệm của hệ phương trình: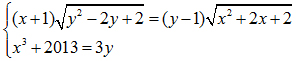


Bài 5.

Cho hàm số . Tính giá trị gần đúng của tổng:
S= f(4) + f(5) + f(6) +…+ f(2013).

Bài 6.

Cho tam giác ABC vuông tại đỉnh A có độ dài cạnh huyền BC = 11cm và . Từ đỉnh A của tam giác ABC vẽ đường phân giác trong AD và đường trung tuyến AM (D, M lần lượt là chân đường phân giác và đường trung tuyến). Tính giá trị gần đúng của diện tích tam giác ADM.

Bài 7.

Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a, gọi (S) là mặt cầu ngoại tiếp hình chóp S.ABCD. Tính giá trị gần đúng của a biết thể tích của khối cầu (S) bằng

Bài 8.

Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; 4) và B(5; 2). Tìm giá trị gần đúng của tọa độ điểm M trên đường thẳng d: x + y – 2 = 0 sao cho góc BAM = 60⁰

Bài 9.

Cho hình chóp có đáy là hình thoi tâm , hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD). Biết , 2cm, khoảng cách từ điểm đến mặt phẳng (SAB) bằng cm. Tính giá trị gần đúng của thể tích khối chóp S.ABCD

Câu 10.

Cho x, y là hai số thực dương. Tính gần đúng giá trị nhỏ nhất của biểu thức: