Đề thi học sinh giỏi lớp 9 THCS tỉnh Phú Thọ năm 2012 - 2013 môn Toán - Có đáp án

SỞ GIÁO DỤC VÀ ĐÀO TẠO PHÚ THỌ ĐỀ CHÍNH THỨC

KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 9 THCS NĂM HỌC 2012-2013 MÔN THI: TOÁN Thời gian làm bài: 150 phút (không kể thời gian giao đề)

Câu 1 (3,0 điểm)

1) Giải phương trình nghiệm nguyên: 8x² - 3xy - 5y = 25

2) Tìm tất cả số nguyên dương n sao cho A = n.4ⁿ + 3n chia hết 7

Câu 2 (4,0 điểm)

1) Rút gọn biểu thức: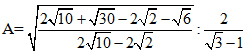

2) Cho các số thực dương a, b, c, x, y, z khác 0 thoả mãn

Chứng minh rằng:

Câu 3 (4,0 điểm)

1) Cho phương trình: x² - 6x - m = 0 (Với m là tham số). Tìm m để phương trình đã cho có hai nghiệm x₁ và x₂ thoả mãn x₁² - x₂² = 12

2) Giải hệ phương trình: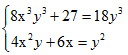

Câu 4 (7,0 điểm)

1) Cho đường tròn (O) đường kính BD = 2R, dây cung AC của đường tròn (O) thay đổi nhưng luôn vuông góc và cắt BD tại H. Gọi P, Q, R, S lần lượt là chân các đường vuông góc hạ từ H xuống AB, AD, CD, CB.

a) Chứng minh rằng: HA² + HB² + HC² + HD² không đổi.

b) Chứng minh rằng: PQRS là tứ giác nội tiếp.

2) Cho hình vuông ABCD và MNPQ có bốn đỉnh M, N, P, Q lần lượt thuộc các cạnh AB, BC, CD, DA của hình vuông. Chứng minh rằng:

Câu 5 (2,0 điểm)

Cho a, b, c là các số thực dương. Chứng minh rằng: