Đề thi thử vào lớp 10 môn Toán chuyên lần 3 năm học 2015-2016 trường THPT Chuyên Nguyễn Huệ, Hà Nội
Đề thi thử vào lớp 10 môn Toán
Đề thi thử vào lớp 10 môn Toán chuyên lần 3 năm học 2015-2016 trường THPT Chuyên Nguyễn Huệ, Hà Nội là đề thi thử vào lớp 10 môn Toán dành cho thí sinh thi vào lớp chuyên Toán và chuyên Tin. Tài liệu này bao gồm đề thi và đáp án, giúp các bạn ôn thi hiệu quả vào trường Chuyên. Mời các bạn cùng tham khảo.
Đề thi thử vào lớp 10 lần 3 năm 2015 môn Ngữ văn điều kiện THPT Chuyên Nguyễn Huệ, Hà Nội
Tuyển tập đề thi vào lớp 10 môn Ngữ văn các tỉnh năm học 2014 - 2015
|
TRƯỜNG THPT CHUYÊN NGUYỄN HUỆ
|
KỲ THI THỬ VÀO LỚP 10 CHUYÊN THPT |
Bài I: (2 điểm)
- Cho a, b, c là các số thực thỏa mãn a2 + b2 + c2 = a + 2b + 3c = 14. Tính giá trị của biểu thức T = abc.
- Cho n là số nguyên dương. Chứng minh A = 24n + 1 + 34n + 2 là hợp số.
Bài II: (3 điểm)
- Giải phương trình 2x2 + 5x - 1 = 7√(x3 - 1).
- Giải hệ phương trình
| { | -5x2 - 14x + y2 - 8 = 0 |
| -5x2 + 16x + y2 - 4xy - 8y + 16 = 0 |
Bài III: (1 điểm)
Cho a, b, c là các số thực dương. Chứng minh
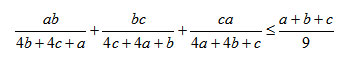
Bài IV: (3 điểm)
Cho đường tròn (O, R) và một điểm S nằm ngoài đường tròn sao cho SO = 2R. Từ S kẻ hai tiếp tuyến SA, SB (A (O), B (O)) và cát tuyến SCD (C nằm giữa S và D) thay đổi. Gọi K là trung điểm của CD và H là giao điểm của AB và SO.
- Chứng minh 4 điểm C, D, H, O nằm trên một đường tròn.
- Chứng minh AC.BD = 1/2 AB.CD.
- Tìm vị trí của điểm K sao cho 1/KA + 1/KB nhỏ nhất.
Bài V: (1 điểm)
Trong mặt phẳng tọa độ Oxy cho ngũ giác lồi ABCDE có tọa độ các đỉnh là các số nguyên. Chứng minh tồn tại ít nhất một điểm nằm trong ngũ giác đó có tọa độ là các số nguyên.
Đáp án đề thi thử vào lớp 10 môn Toán
Bài I: (2 điểm)
1. Tính giá trị của biểu thức T = abc. (1,0đ)
| Ta có | { | a2 + b2 + c2 = 14 | => { | a2 + b2 + c2 = 14 |
| a + 2b + 3c = 14 | 2a + 4b + 6c = 28 |
→ a2 + b2 + c2 – 2a – 4b – 6c = - 14
↔ (a – 1)2 + (b – 2)2 + (c – 3)2 = 0
↔ a = 1; b = 2; c = 3
T = abc = 6.
2. Chứng minh rằng A = 24n + 1 + 34n + 2 là hợp số. (1,0đ)
A = 2.16n + 81n + 2.
Vì n > 0 nên A > 2 + 1 + 2 = 5 (1)
Vì 2.16n ≡ 2 (mod 5)
81n ≡ 1 (mod 5)
A ≡ 2 + 1 + 2 (mod 5) ≡ 0 (mod 5). (2)
Từ (1) và (2) suy ra với mọi n > 0, A > 5 và A chia hết cho 5 nên A là hợp số.
Bài II: (3 điểm)
1. Giải phương trình 2x2 + 5x - 1 = 7√(x3 - 1). (1,5đ)
Điều kiện x ≥ 1
Ta có 3(x - 1) + 2(x2 + x + 1) = 7 √(x - 1)(x2 + x + 1)
Đặt a = x - 1 ≥ 0; b = x2 + x + 1 > 0 ta được: 3a + 2b = 7√ab ↔ b = 9a hoặc b = 1/4a
Giải phương trình ta tìm được x = 4 ± √6.
2. Giải hệ phương trình (1,5đ)
Ta có:
-5x2 - 14x + y2 - 8 = 0 (1)
-5x2 + 16x + y2 - 4xy - 8y + 16 = 0 (2)
Coi (2) là phương trình bậc 2 ẩn y, suy ra: Δ = 9x2
Với y = 5x + 4 suy ra: (5x + 4)2 = 5x2 + 14x + 8 ta được nghiệm (-1/2; 3/2); (-4/5; 0)
Với y = 4 - x suy ra: (4 - x)2 = 5x2 + 14x + 8 ta được nghiệm ((-11 + 3√17)/4; (27 - 3√17)/4); ((-11 - 3√17)/4; (27 + 3√17)/4).
Bài III: (1 điểm)
Chứng minh bất đẳng thức
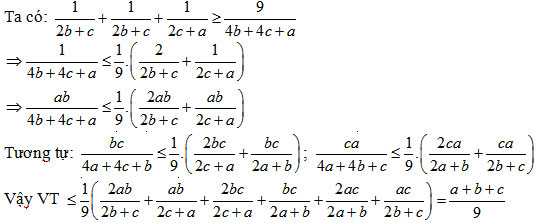
Dấu “ = ” xảy ra khi và chỉ khi a = b = c





