Đề thi tuyển sinh lớp 10 THPT TP Hà Nội môn Toán - Có đáp án
Đề thi tuyển sinh lớp 10 môn Toán
Nhằm giúp các bạn chuẩn bị thật tốt kiến thức để làm bài thi đạt hiệu quả cao, Vndoc.com xin giới thiệu: Đề thi tuyển sinh lớp 10 THPT TP Hà Nội năm học 2013 - 2014 môn Toán - Có đáp án. Đây là tài liệu ôn thi vào lớp 10 môn Toán hay, giúp các em học sinh tự luyện đề, làm quen với các dạng bài thi vào lớp 10. Mời các bạn tham khảo.
Đề thi tuyển sinh vào lớp 10 môn Toán năm học 2015-2016 Sở GD-ĐT TP Hồ Chí Minh
Đề thi - Đáp án thi tuyển sinh lớp 10 THPT tỉnh Thanh Hóa năm 2014 - 2015
Ôn thi vào lớp 10 môn Văn online
|
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ CHÍNH THỨC |
KỲ THI TUYỂN SINH LỚP 10 THPT MÔN THI: TOÁN |
Bài I (2,0 điểm)
Với x > 0, cho hai biểu thức
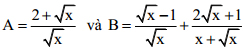
1) Tính giá trị của biểu thức A khi x = 64.
2) Rút gọn biểu thức B.
3) Tìm x để ![]()
Bài II (2,0 điểm) Giải bài toán bằng cách lập phương trình:
Quãng đường từ A đến B dài 90 km. Một người đi xe máy từ A đến B. Khi đến B, người đó nghỉ 30 phút rồi quay trở về A với vận tốc lớn hơn vận tốc lúc đi là 9 km/h. Thời gian kể từ lúc bắt đầu đi từ A đến lúc trở về đến A là 5 giờ. Tính vận tốc xe máy lúc đi từ A đến B.
Bài III (2,0 điểm)
1) Giải hệ phương trình: 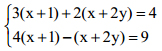
2) Cho parabol ![]() và đường thẳng
và đường thẳng ![]()
a) Với m = 1, xác định tọa độ các giao điểm A, B của (d) và (P).
b) Tìm các giá trị của m để (d) cắt (P) tại hai điểm phân biệt có hoành độ x1, x2 sao cho |x1 - x2| = 2
Bài IV (3,5 điểm)
Cho đường tròn (O) và điểm A nằm bên ngoài (O). Kẻ hai tiếp tuyến AM, AN với đường tròn (O) (M, N là các tiếp điểm). Một đường thẳng d đi qua A cắt đường tròn (O) tại hai điểm B và C (AB < AC, d không đi qua tâm O).
1) Chứng minh tứ giác AMON nội tiếp.
2) Chứng minh AN2 = AB.AC. Tính độ dài đoạn thẳng BC khi AB = 4 cm, AN = 6 cm.
3) Gọi I là trung điểm của BC. Đường thẳng NI cắt đường tròn (O) tại điểm thứ hai T. Chứng minh MT // AC.
4) Hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau ở K. Chứng minh K thuộc một đường thẳng cố định khi d thay đổi và thỏa mãn điều kiện đề bài.
Bài V (0,5 điểm)
Với a, b, c là các số dương thỏa mãn điều kiện a + b + c + ab + bc + ca = 6abc, chứng minh: ![]()
Đáp án đề thi tuyển sinh lớp 10 môn Toán
Bài I (2,0 điểm)
1) Với x = 64 ta có
![]()
2) 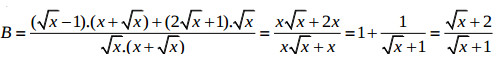
3) Với x > 0 ta có:
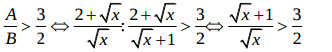
↔ 2√x + 2 > 3√x ↔ √x < 2 ↔ 0 < x < 4 (Do x > 0)
Bài II: (2,0 điểm)
Đặt x (km/h) là vận tốc đi từ A đến B, vậy vận tốc đi từ B đến A là x + 9 (km/h)
Do giả thiết ta có:
90/x + 90/(x + 9) = 5 - 1/2 ↔ 10/x + 10/(x + 9) = 1/2 ↔ x(x + 9) = 20(2x + 9)
↔ x2 - 31x - 180 = 0 ↔ x = 36 (vì x > 0)




