Đề thi tuyển sinh vào lớp 10 THPT môn Toán sở GD&ĐT Phú Thọ năm 2015 - 2016
Đề thi tuyển sinh vào lớp 10 THPT môn Toán
Đề thi tuyển sinh vào lớp 10 THPT môn Toán sở GD&ĐT Phú Thọ năm 2015 - 2016 được VnDoc sưu tầm và đăng tải là tài liệu tham khảo hữu ích dành cho các bạn học sinh lớp 9, giúp các bạn ôn tập và nâng cao kiến thức môn Toán, chuẩn bị cho kì thi tuyển sinh vào lớp 10 hiệu quả. Đề thi có đáp án, mời các bạn tham khảo.
Đề thi tuyển sinh lớp 10 chuyên môn Toán sở GD&ĐT Thái Bình năm 2015 - 2016
Đề thi tuyển sinh vào lớp 10 THPT môn Ngữ văn trường THPT chuyên Thái Nguyên năm 2015 - 2016
| SỞ GIÁO DỤC VÀ ĐÀO TẠO PHÚ THỌ |
KỲ THI TUYỂN SINH VÀO LỚP 10 TRUNG HỌC PHỔ THÔNG NĂM HỌC 2015-2016 Môn Toán Thời gian làm bài: 120 phút, không kể thời gian giao đề Đề thi có 01 trang |
Câu 1 (2,0 điểm)
a) Giải phương trình: x + 2015 = 2016
b) Trong các hình sau, hình nào nội tiếp đường tròn: Hình vuông; hình chữ nhật; hình thang cân; hình thang vuông.
Câu 2 (2,0 điểm) Cho hệ phương trình:
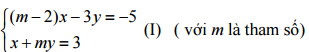
a) Giải hệ phương trình (I) với m=1.
b) Chứng minh hệ phương trình (I) có nghiệm duy nhất với mọi m. Tìm nghiệm duy nhất đó theo m.
Câu 3 (2,0 điểm)
Cho Parabol (P): y = x2 và đường thẳng (d) có phương trình: y = 2(m + 1)x - 3m + 2
a) Tìm tọa độ giao điểm của (P) và (d) với m=3.
b) Chứng minh (P) và (d) luôn cắt nhau tại hai điểm phân biệt A, B với mọi m.
c) Gọi x1, x2 là hoành độ giao điểm A, B. Tìm m để x12 + x22 = 20
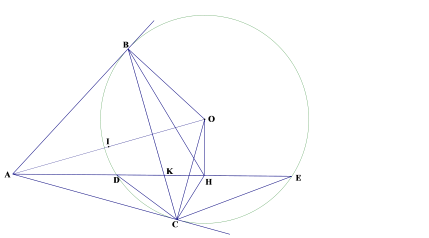
Câu 4 (3,0 điểm) Cho đường tròn (O; R) dây DE < 2R. Trên tia đối DE lấy điểm A, qua A kẻ hai tiếp tuyến AB và AC với đường tròn (O), (B, C là tiếp điểm). Gọi H là trung điểm DE, K là giao điểm của BC và DE.
a) Chứng minh tứ giác ABOC nội tiếp.
b) Gọi (I) là đường tròn ngoại tiếp tứ giác ABOC. Chứng minh rằng H thuộc đường tròn (I) và HA là phân giác ![]()
c) Chứng minh rằng: ![]()
Câu 5 (1,0 điểm) Cho ba số thực dương a, b, c thỏa mãn:
![]()
Tìm giá trị lớn nhất của biểu thức: ![]()
Đáp án đề thi tuyển sinh vào lớp 10 THPT môn Toán
Câu 1:
a) x + 2015 = 2016 <=> x = 2016 - 2015 <=> x = 1 (0,25đ)
Vậy phương trình có nghiệm x = 1 (0,25đ)
b) Hình vuông, hình chữ nhật, hình thang cân (1,5đ)
Câu 2:
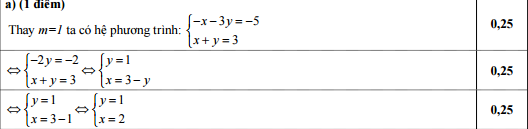

Câu 3:
a) Thay m = 3 ta có (d): y = 8x - 7(0,25đ)
Phương trình hoành độ giao điểm (P) và (d) khi m = 3 là: x2 = 8x - 7 <=> x2 - 8x + 7 = 0 (0,25đ)
Giải phương trình x1 = 1; x2 = 7 (0,25đ)
Tọa độ giao điểm (P) và (d) là (1; 1); (7; 49) (0,25đ)
b) Xét phương trình hoành độ giao điểm (P) và (d): x2 - 2(m + 1)x + 3m - 2 = 0 (0,25đ)
![]()
Nên phương trình (1) có hai nghiệm phân biệt mọi m. Suy ra (P) và (d) luôn cắt nhau tại hai điểm phân biệt A, B với mọi m (0,25đ)

Câu 4:

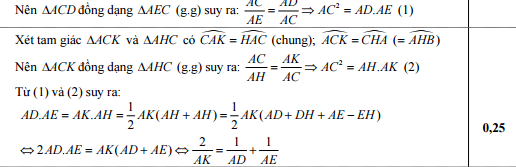
Câu 5: