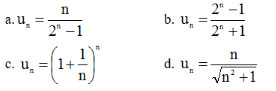Giải bài tập Toán 11 bài 2: Dãy số
Giải Toán 11 Giải tích: Dãy số
VnDoc xin giới thiệu tới bạn đọc tài liệu Giải bài tập Toán 11 bài 2: Dãy số, nội dung tài liệu bao gồm 5 bài tập trang 92 SGK kèm theo lời giải chi tiết sẽ là nguồn thông tin hữu ích để phục vụ các bạn học sinh có kết quả cao hơn trong học tập. Mời thầy cô cùng các bạn học sinh tham khảo.
- Giải bài tập trang 17, 18 SGK Giải tích 11: Hàm số lượng giác
- Giải bài tập Toán 11 ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác
- Giải bài tập trang 28, 29 SGK Giải tích 11: Phương trình lượng giác cơ bản
- Giải bài tập Toán 11 ôn tập chương 2: Tổ hợp - xác suất
- Giải bài tập Toán 11 bài 1: Phương pháp quy nạp toán học
Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 11, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 11 sau: Nhóm Tài liệu học tập lớp 11. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.
Giải bài tập Toán 11 Dãy số
Bài 1 (trang 92 SGK Đại số 11): Viết năm số hạng đầu của dãy số có số hạng tổng quát un cho bởi công thức:
Hướng dẫn giải
Ứng với mỗi giá trị của n ta thu được một số hạng của dãy số. Thay n = 1, 2, 3, 4, 5 vào dãy số đã cho ta được kết quả bài toán.
Lời giải:
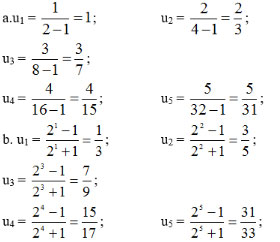
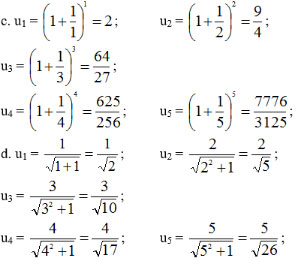
Bài 2 (trang 92 SGK Đại số 11): Cho dãy số (un), biết 
\(u_1 = - 1\), un+ 1 = un + 3 với n ≥ 1.
a. Viết năm số hạng đầu của dãy số;
b. Chứng minh bằng phương pháp quy nạp: \(u_n = 3n – 4\)
Hướng dẫn giải
a. Thay n = 1 vào dãy số ta được \(u_2=u_1+3\), thay giá trị \(u_1\) vào biểu thức ta nhận được \(u_2\)
Tương tự thay n = 2, 3, 4 vào dãy số ta được\(u_3=u_2+3,u_4=u_3+3,u_5=u_4+3\)rồi thay lần lượt theo thứ tự \(u_2,u_3,u_4\) vào biểu thức.
Ta được năm số hạng đầu của dãy số.
b. Các bước để chứng minh quy nạp:
- Quy trình 3 bước:
+ Bước cơ sở: Chứng minh A(0) đúng.
+ Bước quy nạp: Chứng minh với tất cả các số thứ tự bất kì tiếp theo n + 1
A(n + 1) là hệ quả của A(n).
+ Bước giới hạn: Chứng minh rằng với mọi thứ tự giới hạn k, A(k) là hệ quả của A(m) với mọi m < k.
Lời giải:
a. u1 = - 1, un+ 1 = un + 3 với n > 1
u1 = - 1 ; u2 = u1 + 3 = - 1 + 3 = 2
Ta có: u3 = u2 + 3 = 2 + 3 = 5
u4 = u3 + 3 = 5 + 3 = 8
u5 = u4 + 3 = 8 + 3 = 11
b. Chứng minh phương pháp quy nạp: un = 3n – 4 (1)
Khi n = 1 thì u1 = 3.1 - 4 = - 1, vậy (1) đúng với n = 1.
Giả sử công thức (1) đúng với n = k > 1 tức là uk = 3k – 4 (2)
Ta phải chứng minh (1) đúng với n = k + 1, tức là uk+1 = 3(k + 1) – 4 = 3k – 1
Theo giả thiết: uk+1 = uk + 3
(2) \(u_{k+1}\)= 3k – 4 + 3 = 3 ( k + 1) – 4
(1) đúng với n = k + 1
Vậy (1) đúng với n ∈ N*
Bài 3 (trang 92 SGK Đại số 11): Dãy số (un) cho bởi u1 = 3, \(u_n+1 = \sqrt{1+u_n^2}\) , n > 1
a. Viết năm số hạng đầu của dãy số.
b. Dự đoán công thức số hạng tổng quát \(u_n\) và chứng minh công thức đó bằng phương pháp quy nạp.
Hướng dẫn giải
a. Tương tự bài 2.
b. Quan sát kết quả câu a ta thấy \(u_n =\sqrt{n+8}\). Chứng minh bằng phương pháp qui nạp
- Quy trình 3 bước:
+ Bước cơ sở: Chứng minh A(0) đúng.
+ Bước quy nạp: Chứng minh với tất cả các số thứ tự bất kì tiếp theo n + 1
A(n + 1) là hệ quả của A(n).
+ Bước giới hạn: Chứng minh rằng với mọi thứ tự giới hạn k, A(k) là hệ quả của A(m) với mọi m < k.
Lời giải:
a. Năm số hạng đầu của dãy số
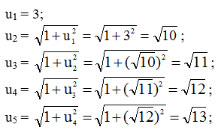
b. Dự đoán công thức số hạng tổng quát của dãy số:
un =\(\sqrt{n+8}\) (1)
Rõ ràng (1) đúng với n = 1
Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)
Vậy (1) đúng với n = k + 1, do đó đúng với mọi n ∈ N*.
Bài 4 (trang 92 SGK Đại số 11): Xét tính tăng, giảm của các dãy số (un), biết:
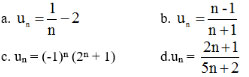
Hướng dẫn giải
♦ Dãy số (\(u_n\)) gọi là dãy tăng nếu \(u_n\) < \(u_n\)+1 ∀n ∈ \(\mathbb{N}^*\)
♦ Dãy số (\(u_n\)) gọi là dãy giảm nếu \(u_n\) > \(u_n\)+1 ∀n ∈ \(\mathbb{N}^*\)
Lời giải:
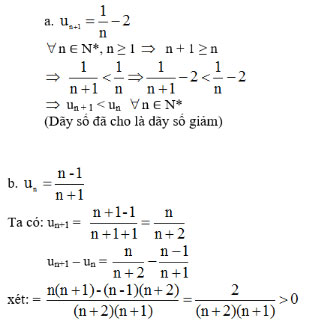
∀n ∈ N*, n ≥ 1 => un+1 – un > 0
=> un+1 > un => (un) là dãy số tăng
c. un = (-1)n(2n + 1)
Nhận xét:
{(-1)n > 0 nếu n chẵn {un > 0 nếu n chẵn
{(-1)n < 0 nếu n lẻ {un < 0 nếu n lẻ
Và \(2^n\)+ 1 > 0 ∀ n ∈ N*
=>u1 < 0, u2 > 0, u3 < 0, u4> 0,…
=>u1 < u2, u2 > u3, u3 < u4,…
=> Dãy số (un) không tăng, không giảm.
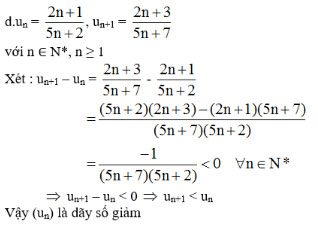
Bài 5 (trang 92 SGK Đại số 11): Trong các dãy số (un) sau, dãy nào bị chặn dưới, bị chặn trên và bị chặn?
Hướng dẫn giải
♦ Dãy số (\(u_n\)) gọi là dãy bị chặn trên nếu có một số thực sao cho \(u_n\) < M ∀n ∈ \(\mathbb{N}^*\)
♦ Dãy số (\(u_n\)) gọi là dãy bị chặn dưới nếu có một số thực sao cho \(u_n\) > m ∀n ∈ \(\mathbb{N}^*\)
♦ Dãy số vừa bị chặn trên vừa bị chặn dưới gọi là dãy bị chặn, tức là tồn tại số thực dương M sao cho |\(u_n\) | < M ∀n ∈ \(\mathbb{N}^*\)
Lời giải:
a. un = 2n2 – 1
Ta có: n ≥ 1
<=> n2 ≥ 1 <=> 2n2 ≥ 2 <=> 2n2 -1≥1
Hay un ≤ 1
=> dãy (un) bị chặn dưới ∀n ∈ N*.
Nhưng (un) không bị chặn trên vì không có số M nào thỏa:
un = 2n2 – 1 ≤ M ∀n ∈N*.
Vậy dãy số (un) bị chặn dưới và không bị chặn trên nên không bị chặn.
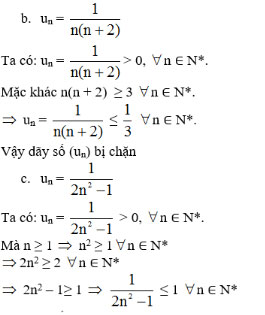
Vậy dãy số vừa bị chặn dưới vừa bị chặn trên, do đó bị chặn.
d. un = sin n + cos n
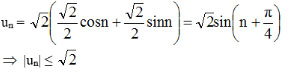
Vậy dãy số (un) bị chặn n ∈ N*
------------------------------------
Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải bài tập Toán 11 bài 2: Dãy số. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Hóa học lớp 10, Giải bài tập Hóa học lớp 11, Hóa học lớp 12, Thi thpt Quốc gia môn Văn, Thi thpt Quốc gia môn Lịch sử, Thi thpt Quốc gia môn Địa lý, Thi thpt Quốc gia môn Toán, đề thi học kì 1 lớp 11, đề thi học kì 2 lớp 11 mà VnDoc tổng hợp và đăng tải.
