Hình học 11 bài 1: Đại cương về đường thẳng và mặt phẳng
Đại cương về đường thẳng và mặt phẳng
Hình học 11 bài 1: Đại cương về đường thẳng và mặt phẳng được VnDoc biên soạn bao gồm hướng dẫn lý thuyết và hướng dẫn giải cho từng bài tập sách giáo khoa và sách bài tập giúp các bạn học sinh luyện tập và hiểu rõ hơn về phần đường thẳng và mặt phẳng trong không gian. Qua đó giúp các bạn học sinh ôn tập, củng cố và rèn luyện thêm kiến thức đã học trong chương trình Toán 11, Mời các bạn học sinh và quý thầy cô cùng tham khảo chi tiết.
Toán 11 Bài 1: Đại cương về đường thẳng và mặt phẳng
A. Lý thuyết về đường thẳng và mặt phẳng
1. Định nghĩa điểm, đường thẳng và mặt phẳng
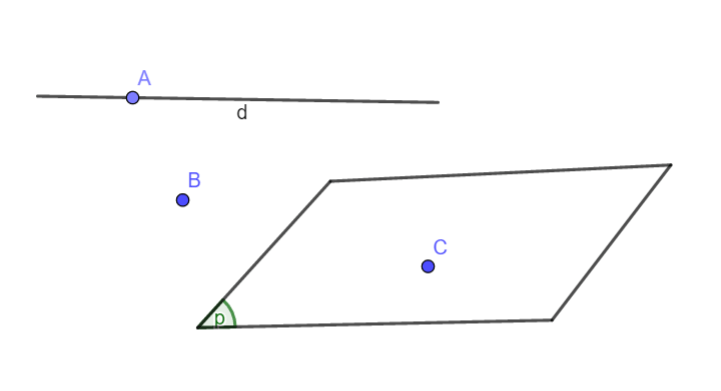
Nhìn vào hình vẽ ta có:
- Điểm A thuộc đường thẳng d, kí hiệu
\(A\in d\) - Điểm C thuộc mặt phẳng (P), kí hiệu \(C\in(P)\)
- Điểm B không thuộc đường thẳng d, không thuộc mặt phẳng (P), kí hiệu: \(B\notin d, B \notin(P)\)
2. Các tính chất
- Có một và chỉ một đường thảng đi qua hai điểm.
- Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.
- Nếu một đường thẳng có hai điểm phân biệt cùng thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
- Có bốn điểm không cùng thuộc một mặt phẳng.
- Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa.
- Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.
3. Cách xác định một mặt phẳng
Một mặt phẳng được xác định nếu:
- Mặt phẳng đi qua ba điểm không thẳng hàng.
- Mặt phẳng đi qua một điểm và một đường thẳng không đi qua điểm đó.
- Mạt phẳng đi qua hai đường thẳng cắt nhau.
4. Giao tuyến của hai mặt phẳng
- Giả sử (P), (Q) là hai mặt phẳng phân biệt có điểm chung A. Khi đó, (P), (Q) có đường thẳng chung duy nhất d đi qua A. Đường thẳng d được gọi là giao tuyến của hai mặt phẳng.
- Đường thẳng d được gọi là giao tuyến của hai mặt phẳng (P), (Q), kí hiệu \(d=(P)\cap (Q)\).
Câu 1. Cho hình lăng trụ \(ABC.A'B'C'\). Gọi \(M;M'\) lần lượt là trung điểm của \(BC\) và \(B'C'\). Xác định giao của \(AM'\) với \((A'BC)\).
Hướng dẫn giải:
Hình vẽ minh họa
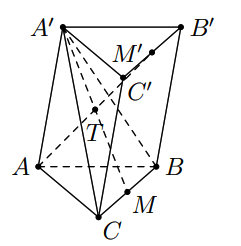
Vì \(M;M'\) là trung điểm của \(BC\) và \(B'C'\) nên \(MM'//BB'//CC'//AA'\)
Suy ra \(A;A';M';M\) cùng thuộc một mặt phẳng.
Trong mặt phẳng \((AA'M'M)\) gọi \(T\) là giao điểm của \(A'M\) và \(AM'\).
Ta có: \(\left\{ \begin{matrix}
A'M \cap AM' \equiv T \\
A'M \subset (A'BC) \\
\end{matrix} \right.\)
\(\Rightarrow AM' \cap (A'BC) =
A'M \cap AM' = T\)
Vậy giao của \(AM'\) với \((A'BC)\) là giao của \(AM'\) với \(A'M\).
Câu 2. Cho hình chóp tứ giác \(S.ABCD\). Gọi \(A_{1}\) là trung điểm của \(SA\), \(B_{1} \in
SB\). Xác định các giao tuyến của mặt phẳng \(\left( A_{1}B_{1}C \right)\) với các mặt của hình chóp. Khi đó hình tạo bởi các giao tuyến trên là hình gì?
A. Tam giác B. Tứ giác
C. Tam giác hoặc tứ giác D. Tứ giác hoặc ngũ giác
Hướng dẫn giải:
Trường hợp 1:
Hình vẽ minh hoạ
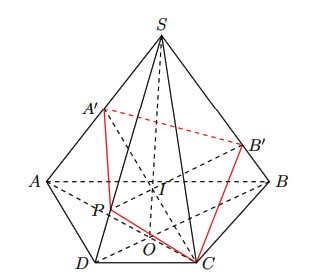
Nếu \(B_{1} \neq S\). Gọi \(O = AC \cap BD,\ I = SO \cap A_{1}C\)
Nếu \(P = IB_{1} \cap SD\)
=> Hình tạo bởi các giao tuyến của mặt phẳng \(\left( A_{1}B_{1}C \right)\) với hình chóp là tứ giác \(A_{1}B_{1}CP\)
Nếu \(P = IB \cap BD\). Gọi \(Q = CP \cap AD\) Thiết diện của mặt phẳng \(\left( A_{1}B_{1}C \right)\) với hình chóp là tứ giác \(A_{1}B_{1}CQ\)
Trường hợp 2:
Hình vẽ minh hoạ
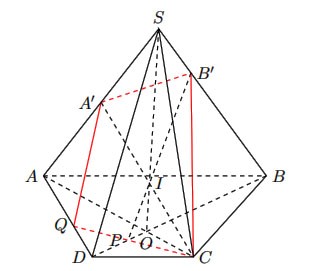
Nếu \(B_{1} \equiv S\). Hình tạo bởi các giao tuyến của mặt phẳng \(\left(
A_{1}B_{1}C \right)\) với hình chóp là tam giác \(SAC\).
Vậy hình tạo bởi các giao tuyến trên có thể là tứ giác hoặc tam giác.
Câu 3. Cho hình chóp \(S.ABCD\) có đáy là hình bình hành \(ABCD\). Gọi \(M \in CD;(M \neq C;M \neq D)\). Giả sử mặt phẳng \((\alpha)\) đi qua \(M\) và song song với \(SC;AC\). Xác định các giao tuyến của mặt phẳng \((\alpha)\) với hình chóp. Hình tạo bởi các giao tuyến trên là hình gì?
A. Tam giác B. Hình vuông
C. Hình bình hành D. Hình thang
Hướng dẫn giải:
Hình vẽ minh họa
Ta có: \(\left\{ \begin{matrix}
(\alpha) \cap (ABCD) = M \\
(\alpha)//AC \\
AC \subset (ABCD) \\
\end{matrix} \right.\)
\(\Rightarrow (\alpha) \cap (ABCD) =
Mx//AC\) và \(Mx \cap AD =
N\)
Tương tự ta cũng có \((\alpha) \cap (SDC) =
MP//SC\)
Khi đó \((\alpha) \cap (SAD) =
NP\)
=> Hình tạo bởi các giao tuyến của (α) với hình chóp là tam giác MNP.
5. Các quy tắc vẽ hình, biểu diễn của hình không gian
- Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.
- Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, của hai đường thẳng cắt nhau là hai đường thẳng cắt nhau.
- Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.
- Đường nhìn thấy vẽ nét liền, đường che khuất vẽ nét đứt.
B. Giải Toán 11 bài 1 SGK
Trong Sách giáo khoa Toán lớp 11, các bạn học sinh chắc hẳn sẽ gặp những bài toán khó, phải tìm cách giải quyết. Hiểu được điều này, VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho các bài tập trong Sách giáo khoa Toán lớp 11. Mời các bạn học sinh tham khảo:
C. Giải Toán 11 bài 1 SBT
Sách bài tập Toán 11 tổng hợp các bài Toán từ cơ bản tới nâng cao, đi kèm với đó là đáp án. Tuy nhiên, nhiều đáp án không được giải chi tiết khiến cho các bạn học sinh gặp nhiều khó khăn khi tiếp xúc với dạng bài mới. VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho từng dạng bài tập trong Sách bài tập để các bạn có thể nắm vững, hiểu rõ hơn về dạng bài tập này. Mời các bạn học sinh tham khảo:
------------------------------------
Đại cương về đường thẳng và mặt phẳng là bước đầu tiên giúp học sinh làm quen với tư duy không gian – một kỹ năng quan trọng trong hình học 11. Hy vọng với nội dung bài học chi tiết và hệ thống bài tập minh họa kèm lời giải trong bài viết, bạn đã có thể hiểu rõ và ghi nhớ những kiến thức trọng tâm. Đừng quên luyện tập thường xuyên để thành thạo hơn khi làm bài kiểm tra và chuẩn bị tốt cho các kỳ thi lớn.
