Toán 11 Bài 3: Đường thẳng vuông góc với mặt phẳng
Lý thuyết Toán 11 Bài 3
VnDoc.com xin gửi tới bạn đọc bài viết Toán 11 Bài 3: Đường thẳng vuông góc với mặt phẳng để bạn đọc cùng tham khảo và có thêm tài liệu học tập nhé.
I. Định nghĩa
- Đường thẳng d được gọi là vuông góc vơi mặt phẳng (α) nếu d vuông góc với mọi đường thẳng a nằm trong mặt phẳng (α).

- Khi d vuông góc với (α) ta còn nói (α) vuông góc với d hoặc d và (α) vuông góc với nhau và kí hiệu là d ⊥(α)
II. Điều kiện để đường thẳng vuông góc mặt phẳng
- Định lí: Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
- Hệ quả. Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì nó cũng vuông góc với cạnh thứ ba của tam giác đó.
Ví dụ 1. Cho tứ diện ABCD có hai tam giác ABC và ABD là các tam giác đều. Gọi I là trung điểm của AB. Chứng minhh AB vuông góc với mặt phẳng (CDI).
Lời giải
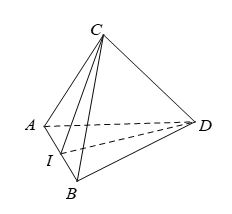
Khi đó, AB ⊥ (CDI) trong đó I là trung điểm của AB.
Thật vậy, vì ABC và ABD là các tam giác đều nên đường trung tuyến đồng thời là đường cao: CI ⊥ AB; DI ⊥ AB
Suy ra: AB ⊥ (CDI).
III. Tính chất.
- Tính chất 1. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
- Mặt phẳng trung trực của một đoạn thẳng.
Người ta gọi mặt phẳng đi qua trung điểm I của đoạn thẳng AB và vuông góc với đường thẳng AB là mặt phẳng trung trực của đoạn thẳng AB.
- Tính chất 2. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
IV. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng.
- Tính chất 1.
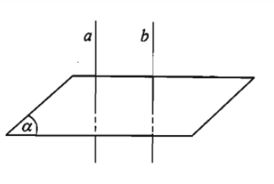
a) Cho hai đường thẳng song song.Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
- Tính chất 2.
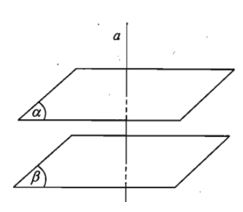
a) Cho hai mặt phẳng song song. Đường thẳng nào vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.
b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
- Tính chất 3.
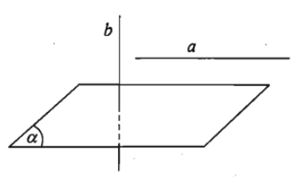
a) Cho đường thẳng a và mặt phẳng (α) song song với nhau. Đường thẳng nào vuông góc với (α) thì cũng vuông góc với a.
b) Nếu một đường thẳng và một mặt phẳng ( không chứa đường thẳng đó) cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.
Ví dụ 2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA⊥(ABCD). Gọi I; J; K lần lượt là trung điểm của AB, BC và SB. Chứng minh:
a) (IJK) // (SAC).
b) BD ⊥ (SAC)
c) BD ⊥ (IJK).
Lời giải:
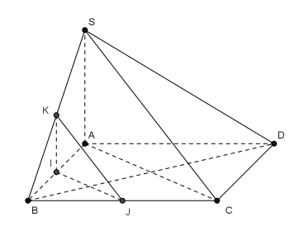
a) Tam giác ABC có IJ Là đường trung bình của tam giác nên IJ // AC (1)
Tam giác SAB có IK là đường trung bình của tam giác nên IK // SA (2)
Từ (1) và (2) suy ra: (IJK) // (SAC) .
b) Do BD⊥ AC; BD⊥SA
Mà BD, AC ⊂ (SAC) nên BD⊥(SAC)
c) Do BD⊥(SAC) và (IJK) // ( SAC) nên BD⊥(IJK)
V. Phép chiếu vuông góc và định lí ba đường vuông góc.
1. Phép chiếu vuông góc.
Cho đường thẳng ∆ vuông góc với mặt phẳng (α). Phép chiếu song song theo phương của ∆ lên mặt phẳng (α) được gọi là phép chiếu vuông góc lên mặt phẳng (α).
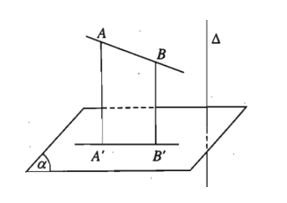
Nhận xét: Phép chiếu vuông góc lên một mặt phẳng là trường hợp đặc biệt của phép chiếu song song nên có đầy đủ các tính chất của phép chiếu song song.
2. Định lí ba đường vuông góc.
Cho đường thẳng a nằm trong mặt phẳng (α) và b là đường thẳng không thuộc (α) đồng thời không vuông góc với (α). Gọi b’ là hình chiếu vuông góc của b trên (α). Khi đó, a vuông góc với b khi và chỉ khi a vuông góc với b’.
3. Góc giữa đường thẳng và mặt phẳng.
Định nghĩa:
Cho đường thẳng d và mặt phẳng (α).
+ Trường hợp đường thẳng d vuông góc với mặt phẳng (α) thì ta nói rằng góc giữa đường thẳng d và mặt phẳng (α) bằng 900.
+ Trường hợp đường thẳng d không vuông góc với mặt phẳng (α) thì góc giữa d và hình chiếu d’ của nó trên (α) gọi là góc giữa đường thẳng d và mặt phẳng (α).
Khi d không vuông góc với (α) thì d cắt (α) tại điểm O, ta lấy một điểm A tùy ý trên d khác điểm O. Gọi H là hình chiếu vuông góc của A lên (α) và φ là góc giữa d và (α) thì ![]() \(\hat{AOH}\) = φ
\(\hat{AOH}\) = φ
- Chú ý: Nếu là góc giữa d và mặt phẳng (α) thì ta luôn có: 00 ≤ φ ≤ 900.
Ví dụ 3. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên ( ABC) trùng với trung điểm BC. Biết SB = a. Tính số đo của góc giữa SA và ( ABC).
Lời giải:

Gọi H là trung điểm của BC.
Vì tam giác ABC vuông góc tại A có đường trung tuyến AH nên suy ra AH = BH = CH = ![]() \(\frac{1}{2}\)BC =
\(\frac{1}{2}\)BC = ![]() \(\frac{a}{2}\)
\(\frac{a}{2}\)
Ta có:
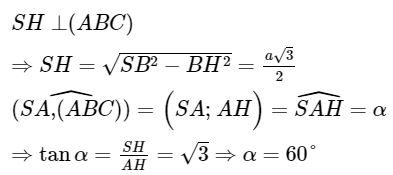
Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Bài 3: Đường thẳng vuông góc với mặt phẳng. Hi vọng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán lớp 11. Mời các bạn cùng tham khảo thêm Lý thuyết Toán 11...









