VnDoc.com

Lí thuyết và bài tập hàm số lượng giác

Hàm số lượng giác Toán 11

Bài trước

Bài sau

Lớp: Lớp 11

Môn: Toán

Phân loại: Tài liệu Tính phí

Hàm số lượng giác Toán 11

I. Lí thuyết hàm số lượng giác
II. Các phương pháp giải toán
III. Giải bài tập SGK Toán 11 KNTT
V. Bài tập trắc nghiệm ôn tập hàm số lượng giác
VI. Bài tập tự luận ôn tập hàm số lượng giác

VnDoc.com xin giới thiệu tới quý thầy cô và các bạn học sinh tài liệu tham khảo Lí thuyết và bài tập hàm số lượng giác. Nội dung tài liệu bao gồm lí thuyết hàm số lượng giác trọng tâm chương trình học, hướng dẫn làm bài tập SGK, SBT, các phương pháp giải toán và bài tập trắc nghiệm hàm lượng giác tổng hợp. Tài liệu được VnDoc biên soạn và đăng tải, hi vọng sẽ giúp các bạn ôn tập kiến thức môn Toán hiệu quả, sẵn sàng cho những kì thi sắp tới. Mời các bạn tham khảo và tải về miễn phí tại đây!

Toán 11: Hàm số lượng giác

I. Lí thuyết hàm số lượng giác

1. Các hằng đẳng thức lượng giác

$1.{{\sin }^{2}}x+{{\cos }^{2}}x=1$	$2.\tan x.\cot x=1$
$3.{{\tan }^{2}}x+1=\frac{1}{{{\cos }^{2}}x}$	$4.{{\cot }^{2}}x+1=\frac{1}{{{\sin }^{2}}x}$

2. Tính tuần hoàn của hàm số

Định nghĩa: Hàm số y= f(x) xác định trên tập D được gọi là hàm số tuần hoàn nếu có số $T\ne 0$ sao cho với mọi ta có:

Nếu có số T dương nhỏ nhất thỏa mãn các điều kiện trên thì hàm số đó được gọi là hàm số tuần hoàn với chu kì T

3. Các hàm số lượng giác

a. Hàm số

Tập xác định:
$-1\le \sin x\le 1$
Hàm số đồng biến trên mỗi khoảng , nghịch biến trên mỗi khoảng
Hàm số là hàm số lẻ nên có đồ thị hàm số nhận gốc tọa độ O làm tâm đối xứng
Hàm số là hàm số tuần hoàn với chu kì

b. Hàm số

Tập xác định:
$-1\le \cos x\le 1$
Hàm số đồng biến trên mỗi khoảng , nghịch biến trên mỗi khoảng $\left( -\pi +k2\pi ,k2\pi \right)$
Hàm số là hàm số lẻ nên có đồ thị hàm số nhận Oy làm trục đối xứng
Hàm số là hàm số tuần hoàn với chu kì

c. Hàm số

Tập xác định:
Tập giá trị
là hàm số lẻ
là hàm số tuần hoàn với chu kì $T=\pi$
Hàm số đồng biến trên khoảng Đồ thi nhận mỗi đường thẳng làm một đường tiệm cận

d, Hàm số

Tập xác định:
Tập giá trị
là hàm số lẻ
là hàm số tuần hoàn với chu kì
Hàm số nghịch biến trên khoảng
Đồ thi nhận mỗi đường thẳng làm một đường tiệm cận

II. Các phương pháp giải toán

Dạng 1: Tìm tập xác định của hàm số

Dạng 2: Tìm giá trị lớn nhất, nhỏ nhất của hàm số lượng giác

III. Giải bài tập SGK Toán 11 KNTT

Bài 1.14 trang 30 SGK Toán 11 Kết nối tri thức

Tìm tập xác định của các hàm số sau:

a) $y=\frac{1-cosx}{sinx}$ b) $y=\sqrt{\frac{1+cosx}{2-cosx}}$

Hướng dẫn giải

a) Biểu thức $\frac{1-cosx}{sinx}$ có nghĩa khi sin x ≠ 0, tức là x ≠ kπ, k ∈ ℤ.

Vậy tập xác định của hàm số $y=\frac{1-cosx}{sinx}$ là D = ℝ \ {kπ | k ∈ ℤ}.

b) Biểu thức $\sqrt{\frac{1+cosx}{2-cosx}}$ có nghĩa khi $\sqrt{\frac{1+cosx}{2-cosx}}≥ 0$ và $2-cosx\neq 0$

Vì – 1 ≤ cos x ≤ 1 nên 1 + cos x ≥ 0 với mọi x ∈ ℝ và 2 – cos x ≥ 1 > 0 với mọi x ∈ ℝ.

Do đó, 2 – cos x ≠ 0 với mọi x ∈ ℝ và $\sqrt{\frac{1+cosx}{2-cosx}}≥ 0$ với mọi x ∈ ℝ.

Vậy tập xác định của hàm số $y=\sqrt{\frac{1+cosx}{2-cosx}}$ là D = ℝ.

Bài 1.15 trang 30 SGK Toán 11 Kết nối tri thức

Xét tính chẵn lẻ của các hàm số sau:

a) y = sin 2x + tan 2x; b) y = cos x + sin²x;

c) y = sin x cos 2x; d) y = sin x + cos x.

Hướng dẫn giải

a) Biểu thức sin 2x + tan 2x có nghĩa khi cos 2x ≠ 0 (do $tan2x=\frac{sin2x}{cos2x}$ ), tức là $2x\neq \frac{\pi }{2}+k\pi ,k\in Z\Leftrightarrow x\neq \frac{\pi }{4}+k\frac{\pi }{2},k\in Z$

Suy ra tập xác định của hàm số y = f(x) = sin 2x + tan 2x là D = R \ { $\frac{\pi }{4}+k\frac{\pi }{2}|k\in Z$ }

Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.

Ta có: f(– x) = sin (– 2x) + tan (– 2x) = – sin 2x – tan 2x = – (sin 2x + tan 2x) = – f(x), ∀ x ∈ D.

Vậy y = sin 2x + tan 2x là hàm số lẻ.

b) Tập xác định của hàm số y = f(x) = cos x + sin²x là D = ℝ.

Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.

Ta có: $f(– x) = cos (– x) + sin^{2} (– x) = cos x + (– sin x)^{2}$

$= cos x + sin^{2} x = f(x), ∀ x ∈ D$ .

Vậy y = cos x + sin²x là hàm số chẵn.

c) Tập xác định của hàm số y = f(x) = sin x cos 2x là D = ℝ.

Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.

Ta có: f(– x) = sin (– x) cos (– 2x) = – sin x cos 2x = – f(x), ∀ x ∈ D.

Vậy y = sin x cos 2x là hàm số lẻ.

d) Tập xác định của hàm số y = f(x) = sin x + cos x là D = ℝ.

Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.

Ta có: f(– x) = sin (– x) + cos (– x) = – sin x + cos x ≠ – f(x).

Vậy y = sin x + cos x là hàm số không chẵn, không lẻ.

Bài 1.16 trang 30 SGK Toán 11 Kết nối tri thức

Tìm tập giá trị của các hàm số sau:

a) $y=2sin(x-\frac{\pi }{4})-1$ b) $y=\sqrt{1+cosx}-2$

Hướng dẫn giải

a) Ta có: $-1\leq sin(x-\frac{\pi }{4})\leq 1$ với mọi $x\in R$

$\Leftrightarrow -2\leq 2sin(x-\frac{\pi }{4})\leq 2$ với mọi $x\in R$

$\Leftrightarrow -2-1\leq 2sin(x-\frac{\pi }{4})-1\leq 2-1$ với mọi $x\in R$

$\Leftrightarrow -3\leq 2sin(x-\frac{\pi }{4})-1\leq 1$ với mọi $x\in R$

$\Leftrightarrow -3\leq y\leq 1$ với mọi $x\in R$

Vậy tập giá trị của hàm số $y=2sin(x-\frac{\pi }{4})-1$ là [– 3; 1].

b) Vì – 1 ≤ cos x ≤ 1 với mọi x ∈ ℝ nên 0 ≤ 1 + cos x ≤ 2 với mọi x ∈ ℝ.

Do đó, $0\leq \sqrt{1+cosx}\leq \sqrt{2}$ với mọi x ∈ ℝ.

Suy ra $-2\leq \sqrt{1+cosx}-2\leq \sqrt{2}-2$ với mọi x ∈ ℝ.

Hay $-2\leq y\leq \sqrt{2}-2$ với mọi x ∈ ℝ.

Vậy tập giá trị của hàm số $y=\sqrt{1+cosx}-2$ là $[-2;\sqrt{2}-2]$

Bài 1.17 trang 30 SGK Toán 11 Kết nối tri thức

Từ đồ thị của hàm số y = tan x, hãy tìm các giá trị x sao cho tan x = 0.

Hướng dẫn giải

Ta có đồ thị của hàm số y = tan x như hình vẽ dưới đây.

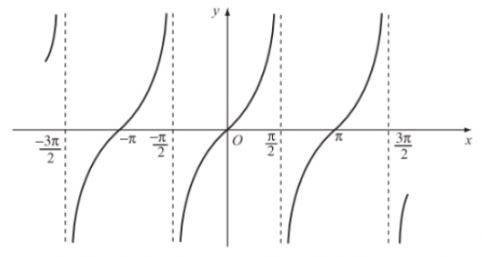
Toán 11 Kết nối tri thức bài 3

Ta có tan x = 0 khi hàm số y = tan x nhận giá trị bằng 0 ứng với các điểm x mà đồ thị giao với trục hoành. Từ đồ thị ở hình trên ta suy ra y = 0 hay tan x = 0 khi x = kπ, k ∈ ℤ.

Bài 1.18 trang 30 SGK Toán 11 Kết nối tri thức

Giả sử khi một cơn sóng biển đi qua một cái cọc ở ngoài khơi, chiều cao của nước được mô hình hóa bởi hàm số h $(t) = 90cos(\frac{\pi }{10}t)$ , trong đó h(t) là độ cao tính bằng centimét trên mực nước biển trung bình tại thời điểm t giây.

a) Tìm chu kì của sóng.

b) Tìm chiều cao của sóng, tức là khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng.

Hướng dẫn giải

a) Chu kì của sóng là $T=\frac{2\pi }{\frac{\pi }{10}}=20$ (giây).

b) Chiều cao của sóng tức là chiều cao của nước đạt được trong một chu kì dao động.

Ta có: $h(20)=90cos(\frac{\pi }{10}\times 20)=90$ (cm).

Vậy chiều cao của sóng là 90 cm.

V. Bài tập trắc nghiệm ôn tập hàm số lượng giác

Câu 1: Hàm số nào sau đây là hàm số chẵn:

$A. y=\sin 5x$	$B.y=3\sin 2x$
$C. y=4\sin x$	$D. y=\left\| \sin x \right\|$

Câu 2: Điều kiện xác định của hàm số là:

$A. x\ne \frac{2\pi }{5}+k2\pi$	$B. x\ne \frac{-2\pi }{5}+k2\pi$
$C. x\ne \frac{2\pi }{5}+k\pi$	$D. x\ne \frac{-2\pi }{5}+k\pi$

Câu 3: Giá trị lớn nhất của hàm số:

Câu 4: Điều kiện xác định của hàm số

$A. x\ne k\pi$
$B. x\ne \frac{\pi }{2}+k2\pi$
$C. x\ne \frac{\pi }{2}+k2\pi$
$D. x\ne k2\pi$

Câu 5: Hàm số có chu kì bằng bao nhiêu?

$A. 7\pi$	$B. 5\pi$
$C. 2\pi$	$D. 10\pi$

Câu 6: Hàm số đồng biến trên khoảng nào sau đây?

$A. \left( 0,\frac{\pi }{3} \right)$	$B. \left( -\frac{\pi }{2},0 \right)$
$C. \left( \frac{\pi }{2},\frac{2\pi }{3} \right)$	$D. \left( 0,\pi \right)$

Câu 7: Trong các hàm sau hàm nào là hàm số chẵn?

$A. y=\sin x$	$B.y=-\cos x$
$C. y=-\sin x$	$D. y=\sin 2x$

Câu 8: Hàm số nghịch biến trên khoảng nào sau đây?

$A. \left( 0,\frac{\pi }{2} \right)$	$C. \left( \frac{\pi }{2},\pi \right)$
$B. \left( 0,\pi \right)$	$D. \left( \frac{7\pi }{6},\frac{3\pi }{2} \right)$

Câu 9: Đồ thị hàm số đi qua điểm nào sau đây?

$A. \left( 0,\frac{\pi }{4} \right)$	$C. \left( \frac{\pi }{4},\frac{\pi }{2} \right)$
$B. \left( -\frac{\pi }{4},0 \right)$	$D. \left( \frac{\pi }{2},-\frac{\pi }{4} \right)$

Câu 10: Hàm số $y=\frac{1-\sin x}{1+\sin x}$ xác định khi và chỉ khi:

$A. x\ne \frac{\pi }{2}+k2\pi$	$C. x\ne \frac{\pi }{2}+k\pi$
$B. x\ne \frac{-\pi }{2}+k2\pi$	$D. x\ne \frac{-\pi }{2}+k\pi$

Câu 11: Hàm số nào sau đây nhận giá trị âm nếu

$A. y=\cot \left( x+\pi \right)$	$B. y=\tan \left( x+\pi \right)$
$C. y=\cos \left( x+\pi \right)$	$D. y=\sin \left( x+\pi \right)$

Câu 12: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số: lần lượt là:

A. 3 và 1 B. 3 và 2 C. 9 và 1 D. 3 và 0

Câu 13: Tập xác định của hàm số:

$A. x\ne \pi +k\pi$	$C. x\ne \frac{k\pi }{4}$
$B. x\ne \frac{k\pi }{3}$	$D. x\ne \frac{k\pi }{2}$

Câu 14: Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số $y=8-4\cos \left( \frac{\pi }{4}-3x \right)$ là:

Câu 15: Mệnh đề nào sau đây đúng?

$A. \sin x\ne 0\Leftrightarrow x\ne \frac{k\pi }{2}$ $B. \sin x=0\Leftrightarrow x=k\pi$
$C. \tan x=0\Leftrightarrow x=\frac{\pi }{2}+k\pi$ $D. \cos x=-1\Leftrightarrow x=\pi +k\pi$

Câu 16: Điều kiện xác định của hàm số: là:

$A. x\ge 1$	$B. x\ne 1$
	$D. x-1\ne 0$

Câu 17: Trong các hàm số sau hàm số nào là hàm số lẻ?

$A. y=-\cos x$	$B. y=\cos 2x$
$C. y=\sin x$	$D. y=\cos x$

Câu 18: Tập giá trị của hàm số là:

$A. \left[ 1,2 \right]$	$B. \left[ -1,2 \right]$
$C. \left[ \frac{3}{4},1 \right]$	$D. \left[ \frac{3}{4},3 \right]$

Câu 19: Điều kiện xác định của hàm số:

$A. x\ne \frac{k\pi }{4}$	$B. x\ne k\pi$
$C. x\ne \frac{k\pi }{2}$	$D. x\ne k2\pi$

Câu 20: Đồ thị hàm số đi qua điểm nào sau đây?

$C. \left( \pi ,1 \right)$ $D. \left( 2,\pi \right)$

Mời các bạn tham khảo đáp án trắc nghiệm tại đây: Đáp án trắc nghiệm hàm số lượng giác

VI. Bài tập tự luận ôn tập hàm số lượng giác

Câu 1. a. Tìm tập xác định của hàm số $y = \sqrt{1 - \sin\ 2x} - \sqrt{1 + sin2x}.$

b. Tìm tập xác định của hàm số $y = \sqrt{5 + 2cot^{2}x - \sin x} + \cot\left( \frac{\pi}{2} + x \right).$

Hướng dẫn giải:

Vì hàm số được cho có các biểu thức chứa căn nên để tìm tập xác định, ta sẽ tìm điều kiện xác định của biểu thức dưới căn phải lớn hơn hoặc bằng 0.

a. Ta có

$- 1 \leq sin2x \leq 1 \Rightarrow \left\{ \begin{matrix} 1 + sin2x \geq 0 \\ 1 - \sin\ 2x \geq 0 \\ \end{matrix} \right.\ ,\forall x\mathbb{\in R}.$

Vậy tập xác định $D\mathbb{= R}.$

b. Hàm số xác định khi và chỉ khi các điều kiện sau thỏa mãn đồng thời:

$5 + 2cot^{2}x - \sin x \geq 0$ , $\cot\left( \frac{\pi}{2} + x \right)$ xác định và $\cot x$ xác định.

Ta có

$\left\{ \begin{matrix} 2cot^{2}x \geq 0 \\ - 1 \leq \sin x \leq 1\overset{}{\rightarrow}5 - \sin x \geq 0 \\ \end{matrix} \right.\ \overset{}{\rightarrow}5 + 2cot^{2}x - \sin x \geq 0,\ \forall x\mathbb{\in R}.$

$\cot\left( \frac{\pi}{2} + x \right)$ xác định $\Leftrightarrow \sin\left( \frac{\pi}{2} + x \right) \neq 0 \Leftrightarrow \frac{\pi}{2} + x \neq k\pi \Leftrightarrow x \neq - \frac{\pi}{2} + k\pi,\ k\mathbb{\in Z}.$

$\cot x$ xác định $\Leftrightarrow \sin x \neq 0 \Leftrightarrow x \neq k\pi,\ k\mathbb{\in Z}.$

Do đó hàm số xác định $\Leftrightarrow \left\{ \begin{matrix} x \neq - \frac{\pi}{2} + k\pi \\ x \neq k\pi \\ \end{matrix} \right.\ \Leftrightarrow x \neq \frac{k\pi}{2},k\mathbb{\in Z}.$

Vậy tập xác định $D\mathbb{= R}\backslash\left\{ \frac{k\pi}{2},k\mathbb{\in Z} \right\}.$

Câu 2. Cho hai hàm số $f(x) = \frac{cos2x}{1 + sin^{2}3x}$ và $g(x) = \frac{|sin2x| - cos3x}{2 + tan^{2}x}$ . Mệnh đề nào sau đây là đúng?

A. lẻ và chẵn. B. và chẵn.

C. chẵn, lẻ. D. và lẻ.

Gợi ý:

Áp dụng tính chẵn lẻ của hàm số và xét biểu thức .

Hướng dẫn giải:

Xét hàm số $f(x) = \frac{cos2x}{1 + sin^{2}3x}.$

TXĐ: $D\mathbb{= R}$ . Do đó $\forall x \in D \Rightarrow - x \in D.$

Ta có

$f( - x) = \frac{\cos( - 2x)}{1 + sin^{2}( - 3x)} = \frac{cos2x}{1 + sin^{2}3x} = f(x)\overset{}{\rightarrow}f(x)$ là hàm số chẵn.

Xét hàm số $g(x) = \frac{|sin2x| - cos3x}{2 + tan^{2}x}.$

TXĐ: $D\mathbb{= R}\backslash\left\{ \frac{\pi}{2} + k\pi\ \left( k\mathbb{\in Z} \right) \right\}$ . Do đó $\forall x \in D \Rightarrow - x \in D.$

Ta có

$g( - x) = \frac{\left| \sin( - 2x) \right| - \cos( - 3x)}{2 + tan^{2}( - x)} = \frac{|sin2x| - cos3x}{2 + tan^{2}x} = g(x)\overset{}{\rightarrow}g(x)$ là hàm số chẵn.

Vậy và chẵn.

Câu 3. a. Tìm chu kì T của hàm số $y = 3cos(2x + 1) - 2sin\left( \frac{x}{2} - 3 \right).$

b. Tìm chu kì của hàm số $y = \sin\left( 2x + \frac{\pi}{3} \right) + 2cos\left( 3x - \frac{\pi}{4} \right).$

Hướng dẫn giải:

a. Hàm số tuần hoàn với chu kì $T_{1} = \frac{2\pi}{2} = \pi.$

Hàm số $y = - 2sin\left( \frac{x}{2} - 3 \right).$ tuần hoàn với chu kì $T_{2} = \frac{2\pi}{\frac{1}{2}} = 4\pi.$

b. Hàm số $y = \sin\left( 2x + \frac{\pi}{3} \right)$ tuần hoàn với chu kì $T_{1} = \frac{2\pi}{2} = \pi.$

Hàm số $y = 2cos\left( 3x - \frac{\pi}{4} \right)$ tuần hoàn với chu kì $T_{2} = \frac{2\pi}{3}.$

Suy ra hàm số $y = \sin\left( 2x + \frac{\pi}{3} \right) + 2cos\left( 3x - \frac{\pi}{4} \right)$ tuần hoàn với chu kì $T = 2\pi.$

Câu 4. Đồ thị hàm số $y = \sin x$ được suy từ đồ thị của hàm số $y = \cos x + 1$ bằng cách:

A. Tịnh tiến qua trái một đoạn có độ dài là $\frac{\pi}{2}$ và lên trên đơn vị.

B. Tịnh tiến qua phải một đoạn có độ dài là $\frac{\pi}{2}$ và lên trên đơn vị.

C. Tịnh tiến qua trái một đoạn có độ dài là $\frac{\pi}{2}$ và xuống dưới đơn vị.

D. Tịnh tiến qua phải một đoạn có độ dài là $\frac{\pi}{2}$ và xuống dưới đơn vị.

Gợi ý:

Áp dụng lý thuyết về phép tịnh tiến đối với đồ thị hàm số.

Nhắc lại lý thuyết:

Cho là đồ thị của hàm số và , ta có:

+ Tịnh tiến lên trên đơn vị thì được đồ thị của hàm số .

+ Tịnh tiến xuống dưới đơn vị thì được đồ thị của hàm số .

+ Tịnh tiến sang trái đơn vị thì được đồ thị của hàm số .

+ Tịnh tiến sang phải đơn vị thì được đồ thị của hàm số .

Ngoài ra ta cần biến đổi hàm y = sin (x) về hàm có chứa cos (x).

Hướng dẫn giải:

Ta có $y = \sin x = \cos\left( \frac{\pi}{2} - x \right) = \cos\left( x - \frac{\pi}{2} \right).$

Tịnh tiến đồ thị $y = \cos x + 1$ sang phải $\frac{\pi}{2}$ đơn vị ta được đồ thị hàm số $y = \cos\left( x - \frac{\pi}{2} \right) + 1.$

Tiếp theo tịnh tiến đồ thị $y = \cos\left( x - \frac{\pi}{2} \right) + 1$ xuống dưới đơn vị ta được đồ thị hàm số $y = \cos\left( x - \frac{\pi}{2} \right).$

Tải thêm tài liệu tại: Chuyên đề toán 11

Trên đây VnDoc đã chia sẻ đến các bạn học sinh Lí thuyết và bài tập hàm số lượng giác nhằm cung cấp cơ sở kiến thức ôn tập cho các bạn học sinh, giúp các bạn tiếp xúc với nhiều dạng bài về hàm số lượng giác. Chúc các bạn ôn tập thật tốt!

Bài học tiếp theo: Phương trình lượng giác cơ bản

Ngoài ra, VnDoc mời bạn đọc tham khảo thêm một số tài liệu liên quan:

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

30 lượt tải tài liệu

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Chia sẻ bởi:
Bơ

3

4.165

Bài trước

Bài sau

Có thể bạn quan tâm

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!