Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Toán 11 Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song

Lí thuyết, Bài tập Hình học lớp 11

Bài trước

Tải về

Bài sau

Lớp: Lớp 11

Môn: Toán

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Hai đường thẳng chéo nhau và hai đường thẳng song song

Lí thuyết và Bài tập hai đường thẳng chéo nhau và hai đường thẳng song song được VnDoc biên soạn bao gồm hướng dẫn lý thuyết và hướng dẫn giải cho từng bài tập sách giáo khoa và sách bài tập giúp các bạn học sinh luyện tập và hiểu rõ hơn về phần đường thẳng và mặt phẳng trong không gian. Qua đó giúp các bạn học sinh ôn tập, củng cố và rèn luyện thêm kiến thức đã học trong chương trình Toán 11, Mời các bạn học sinh và quý thầy cô cùng tham khảo chi tiết.

A. Lí thuyết Đường thẳng và mặt phẳng trong không gian

I. Vị trí tương đối của hai đường thẳng trong không gian

Cho hai đường thẳng a, b trong không gian, có 2 trường hợp xảy ra:

Trường hợp 1: a, b đồng phẳng

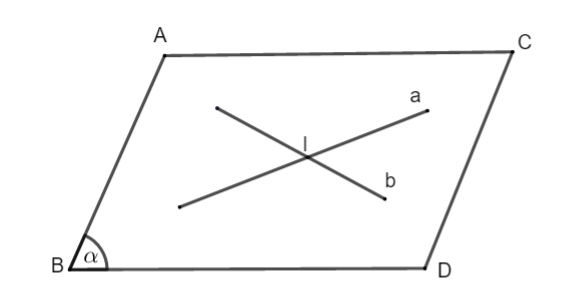
Toán 11 Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song

Đường thẳng a cắt đường thẳng b tại một điểm, $a\cap b=\left\{ I \right\}$

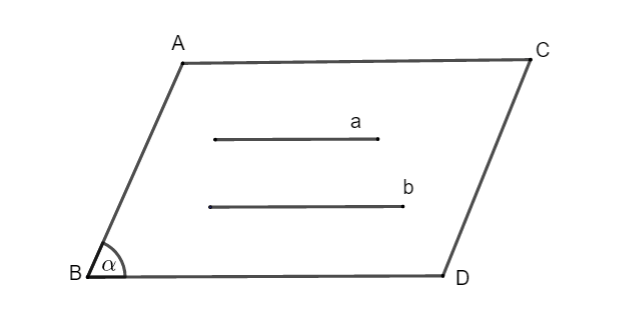
Toán 11 Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song

Đường thẳng a song song với đường thẳng b, a // b

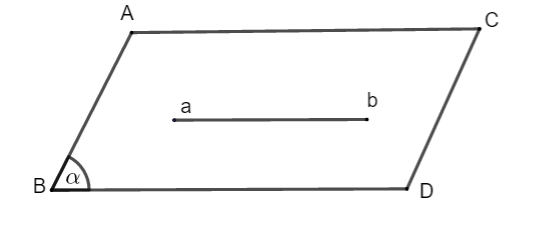
Toán 11 Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song

Đường thẳng a trùng với đường thẳng b, $a\equiv b$

$\Rightarrow$ Hai đường thẳng song song là hai đường thẳng cùng nằm trong một mặt phẳng và không có điểm chung.

Trường hợp 2: a, b không đồng phẳng

Ví dụ 1

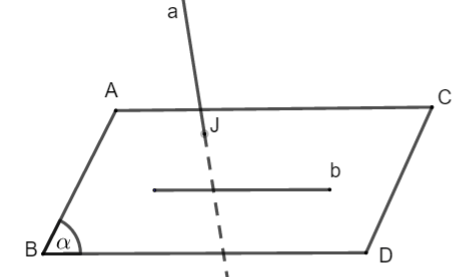Toán 11 Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song

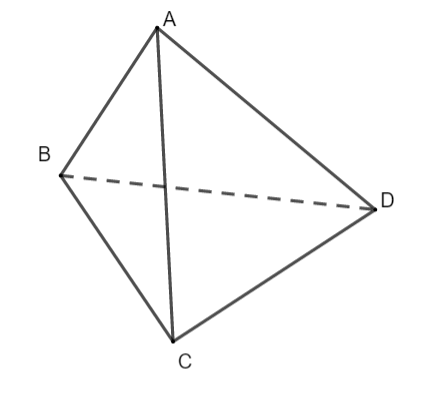
Ví dụ 2

Theo hình vẽ ở trên ta nói a, b chéo nhau hoặc a chéo với b

Ở ví dụ 2 các cặp cạnh chéo nhau là: AC và BD, AB và CD, …

II. Tính chất của hai đường thẳng song song

Dựa vào tiên đề Ơ – clít về hai đường thẳng song song trong mặt phẳng ta có:

Định lí 1: Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng cho trước.

Định lí 2: (giao tuyến của ba mặt phẳng) Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.

$\Rightarrow$ Hệ quả: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

Định lí 3: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.

III. Bài tập ví dụ minh họa Hai đường thẳng song song, chéo nhau

Ví dụ: Cho hình chóp S.ABCD có đáy là hình bình hành. Điểm M thuộc cạnh SA, điểm E và F lần lượt là trung điểm của AB và BC.

1) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD).

2) Xác định giao tuyến của hai mặt phẳng (MBC) và (SAD).

3) Xác định giao tuyến của hai mặt phẳng (MEF) và (SAC).

Hướng dẫn giải

Hình vẽ minh họa

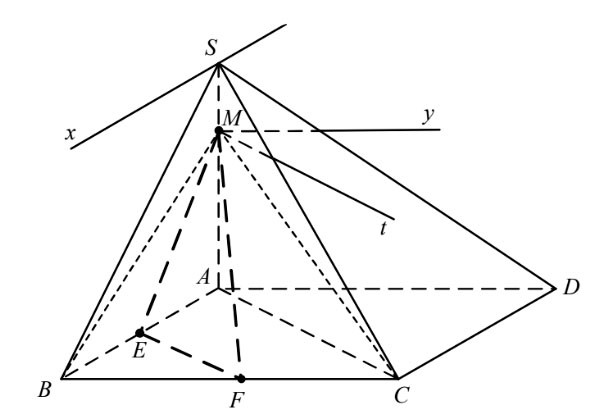
1) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD).

Ta có: $\left\{ \begin{matrix} S \in (SAB) \cap (SCD) \\ AB \subset (SAB);CD \subset (SCD) \\ AB//CD \end{matrix} \right.$

$\Rightarrow Sx = (SAB) \cap (SCD)$ với Sx // AB //CD.

2) Xác định giao tuyến của hai mặt phẳng (MBC) và (SAD).

Ta có: $\left\{ \begin{matrix} M \in SA \subset (SAD) \\ M \in (MBC) \end{matrix} \right.$

$\Rightarrow M \in (MBC) \cap (SAD)$

Lại có: $\left\{ \begin{matrix} M \in (MBC) \cap (SAD) \\ BC \subset (SBC);AD \subset (SAD) \\ BC//AD \end{matrix} \right.$

$\Rightarrow My \in (MBC) \cap (SAD)$ với My // BC // AD.

3) Xác định giao tuyến của hai mặt phẳng (MEF) và (SAC).

Ta có: $\left\{ \begin{matrix} M \in SA \subset (SAC) \\ M \in (MEF) \end{matrix} \right.$

$\Rightarrow M \in (MEF) \cap (SAC)$

Xét tam giác ABC có: EF là đường trung bình của tam giác => EF // AC.

Do $\left\{ \begin{matrix} M \in (MEF) \cap (SAC) \\ EF \subset (MEF);AC \subset (SAC) \\ EF//AC \end{matrix} \right.$

$\Rightarrow Mt \in (MEF) \cap (SAC)$ với Mt // EF // AC.

Ví dụ: Cho hình chóp S.ABC. Lấy điểm I thuộc cạnh SA sao cho IA = 2IS, các điểm M, N lần lượt là trung điểm của SB, SC. Lấy điểm H đối xứng với I qua M, K đối xứng với I qua N.

a) Chứng minh HK // BC b) Chứng minh BH // SA

Hướng dẫn giải

Hình vẽ minh họa

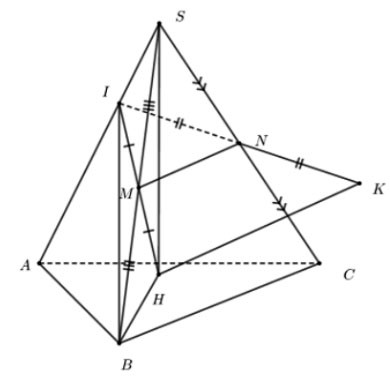
Xét tam giác IHK có MN là đường trung bình => MN // BC (1)

Xét tam giác SBC có MN là đường trung bình => MN // BC (2).

Từ (1) và (2) => HK // BC (đpcm).

b) Tứ giác SIBH có hai đường chéo SB và IH cắt nhau tại M là trung điểm của mỗi đường

=> SIBH là hình bình hành

=> SI // BH => SA // BH (đpcm).

Ví dụ: Cho hình chóp S.ABCD có đáy là tứ giác lồi. Gọi M, N lần lượt là trọng tâm tam giác SAB và SAD. Lấy E là trung điểm của BC.

a) Chứng minh MN // BD

b) Gọi L, H là giao điểm của (MNE) với SD và SB. Chứng minh UT // BD.

Hướng dẫn giải

Gọi Q là trung điểm của SA

Xét tam giác QBD có

$\frac{QN}{DQ} = \frac{QM}{QB} = \frac{1}{3}$ (Theo tính chất trọng tâm tam giác)

Vậy

b) Dựng $EK//MN \Rightarrow (MNE) \equiv (MNKE)$

Tìm $L = (MNE) \cap SB;SB \subset (SAD)$ ; gọi $F = AD \cap KE$

$\Rightarrow H = MP \cap SB$

Ta có: $\left\{ \begin{matrix} MN \subset (MNE) \\ BD \subset (SBD) \\ MN//BD \\ (MNE) \cap (SBD) = LH \end{matrix} \right.$

$\Rightarrow LH//BD//MN$

B. Giải SGK Toán 11 Kết nối tri thức

Trong Sách giáo khoa Toán lớp 11, các bạn học sinh chắc hẳn sẽ gặp những bài toán khó, phải tìm cách giải quyết. Hiểu được điều này, VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho các bài tập trong Sách giáo khoa Toán lớp 11. Mời các bạn học sinh tham khảo:

Giải bài tập SGK Toán 11 KNTT

C. Giải Toán 11 SBT Kết nối tri thức

Sách bài tập Toán 11 tổng hợp các bài Toán từ cơ bản tới nâng cao, đi kèm với đó là đáp án. Tuy nhiên, nhiều đáp án không được giải chi tiết khiến cho các bạn học sinh gặp nhiều khó khăn khi tiếp xúc với dạng bài mới. VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho từng dạng bài tập trong Sách bài tập để các bạn có thể nắm vững, hiểu rõ hơn về dạng bài tập này. Mời các bạn học sinh tham khảo:

Giải sách bài tập Toán 11 KNTT

------------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Toán 11 bài 2: Hai đường thẳng song song và hai đường thẳng chéo nhau. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Hóa học lớp 10, Giải bài tập Hóa học lớp 11, Hóa học lớp 12, Thi THPT Quốc gia môn Văn, Thi THPT Quốc gia môn Lịch sử, Thi THPT Quốc gia môn Địa lý, Thi THPT Quốc gia môn Toán, đề thi học kì 1 lớp 11, đề thi học kì 2 lớp 11 mà VnDoc tổng hợp và đăng tải.

Tải về

Chọn file muốn tải về: