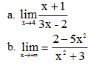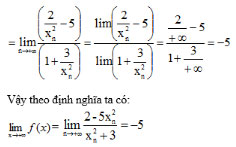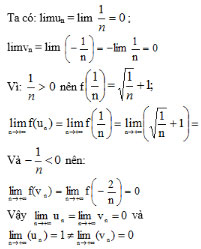VnDoc.com

Giải bài tập Toán 11 bài 2: Giới hạn của hàm số

Giải bài tập môn Toán lớp 11

Bài trước

Tải về

Bài sau

Môn: Toán

Loại File: PDF + Word

Phân loại: Tài liệu Tính phí

Giải bài tập Toán 11 Giải tích: Giới hạn của hàm số

VnDoc xin giới thiệu tới bạn đọc tài liệu Giải bài tập Toán 11 bài 2: Giới hạn của hàm số, nội dung tài liệu gồm 7 bài tập trang 132, 133 SGK kèm theo lời giải chi tiết sẽ giúp các bạn học sinh học tập hiệu quả hơn môn Toán. Mời thầy cô cùng các bạn học sinh tham khảo.

Giải bài tập Toán 11 bài 2: Dãy số

Giải bài tập Toán 11 bài 3: Cấp số cộng

Giải bài tập Toán 11 bài 4: Cấp số nhân

Giải bài tập Toán 11 ôn tập chương 3: Dãy số - Cấp số cộng và cấp số nhân

Giải bài tập Toán 11 Giới hạn của hàm số

Bài 1 (trang 132 SGK Đại số 11): Dùng định nghĩa tìm các giới hạn sau:

Lời giải:

Bài 2 (trang 132 SGK Đại số 11):

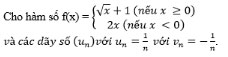
Tính limu_n, limv_n, limf(u_n), limf(v_n).

Từ đó có kết luận gì về giới hạn của hàm số đã cho khi x → 0?

Lời giải:

Bài 3 (trang 132 SGK Đại số 11): Tính các giới hạn sau:

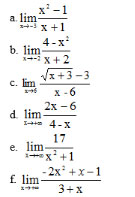
Lời giải:

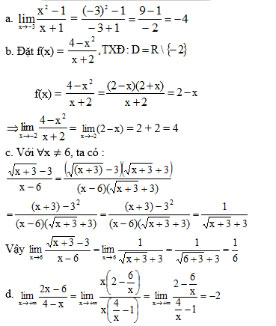
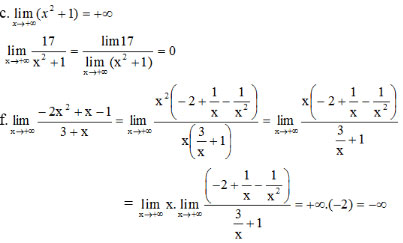
Bài 4 (trang 132 SGK Đại số 11): Tìm các giới hạn sau:

$a) \underset{x\rightarrow 2}{lim}\frac{3x -5}{(x-2)^{2}};$ $a) \underset{x\rightarrow 2}{lim}\frac{3x -5}{(x-2)^{2}};$

$b) \underset{x\rightarrow 1^{-}}{lim}\frac{2x -7}{x-1};$ $b) \underset{x\rightarrow 1^{-}}{lim}\frac{2x -7}{x-1};$

$c) \underset{x\rightarrow 1^{+}}{lim}\frac{2x -7}{x-1}.$ $c) \underset{x\rightarrow 1^{+}}{lim}\frac{2x -7}{x-1}.$

Lời giải:

a) Ta có

$\underset{x\rightarrow 2}{\lim} (x - 2)^2= 0 và (x - 2)^2> 0 với ∀x ≠ 2 và \underset{x\rightarrow 2}{\lim} (3x - 5) = 3.2 - 5 = 1 > 0$ $\underset{x\rightarrow 2}{\lim} (x - 2)^2= 0 và (x - 2)^2> 0 với ∀x ≠ 2 và \underset{x\rightarrow 2}{\lim} (3x - 5) = 3.2 - 5 = 1 > 0$

Do đó $\underset{x\rightarrow 2}{\lim}\frac{3x -5}{(x-2)^{2}} = +∞$ $\underset{x\rightarrow 2}{\lim}\frac{3x -5}{(x-2)^{2}} = +∞$.

b) Ta có

$\underset{x\rightarrow 1^{-}}{\lim} (x - 1)=0 và x - 1 < 0 với ∀x < 1 và \underset{x\rightarrow 1^{-}}{\lim} (2x - 7) = 2.1 - 7 = -5 <0.$ $\underset{x\rightarrow 1^{-}}{\lim} (x - 1)=0 và x - 1 < 0 với ∀x < 1 và \underset{x\rightarrow 1^{-}}{\lim} (2x - 7) = 2.1 - 7 = -5 <0.$

Do đó $\underset{x\rightarrow 1^{-}}{\lim}\frac{2x -7}{x-1} = +∞$ $\underset{x\rightarrow 1^{-}}{\lim}\frac{2x -7}{x-1} = +∞$.

c) Ta có

$\underset{x\rightarrow 1^{+}}{\lim} (x - 1) = 0 và x - 1 > 0 với ∀x > 1 và \underset{x\rightarrow 1^{+}}{\lim} (2x - 7) = 2.1 - 7 = -5 < 0$ $\underset{x\rightarrow 1^{+}}{\lim} (x - 1) = 0 và x - 1 > 0 với ∀x > 1 và \underset{x\rightarrow 1^{+}}{\lim} (2x - 7) = 2.1 - 7 = -5 < 0$

Do đó $\underset{x\rightarrow 1^{+}}{lim}\frac{2x -7}{x-1}= -∞.$ $\underset{x\rightarrow 1^{+}}{lim}\frac{2x -7}{x-1}= -∞.$

Bài 5 (trang 133 SGK Đại số 11): Cho hàm số f(x) = ...

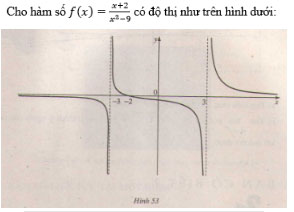
a. Quan sát đồ thị và nêu nhận xét về giá trị hàm số cho khi:

$x →- ∞, x →3^-, x →-3^+$

b. Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:

$\underset{x\rightarrow -\infty }{\lim} f(x) với f(x)$ $\underset{x\rightarrow -\infty }{\lim} f(x) với f(x)$ được xét trên khoảng $(-\infty; -3),$ $(-\infty; -3),$

$\underset{x\rightarrow 3^{-}}{\lim} f(x) với f(x)$ $\underset{x\rightarrow 3^{-}}{\lim} f(x) với f(x)$được xét trên khoảng $(-3,3),$

$\underset{x\rightarrow -3^{+}}{lim} f(x) với f(x)$ $\underset{x\rightarrow -3^{+}}{lim} f(x) với f(x)$ được xét trên khoảng $(-3; 3).$

Lời giải:

a) Quan sát đồ thị ta thấy $x → -∞ thì f(x) → 0; khi x → 3^- thì f(x) → -∞;$

$khi x → -3^+ thì f(x) → +∞.$

$b) \underset{x\rightarrow -\infty }{lim} f(x) = \underset{x\rightarrow -\infty }{lim}\frac{x+2}{x^{2}-9} = \underset{x\rightarrow -\infty }{lim}\frac{\frac{1}{x}+\frac{2}{x^{2}}}{1-\frac{9}{x^{2}}} = 0.$ $b) \underset{x\rightarrow -\infty }{lim} f(x) = \underset{x\rightarrow -\infty }{lim}\frac{x+2}{x^{2}-9} = \underset{x\rightarrow -\infty }{lim}\frac{\frac{1}{x}+\frac{2}{x^{2}}}{1-\frac{9}{x^{2}}} = 0.$

$\underset{x\rightarrow 3^{-}}{lim} f(x) = \underset{x\rightarrow 3^{-}}{lim}\frac{x+2}{x^{2}-9} = \underset{x\rightarrow 3^{-}}{lim}\frac{x+2}{x+3}.\frac{1}{x-3} = -∞ vì \underset{x\rightarrow 3^{-}}{lim}\frac{x+2}{x+3} = \frac{5}{6} > 0 và \underset{x\rightarrow 3^{-}}{\lim} \frac{1}{x-3} = -∞.$ $\underset{x\rightarrow 3^{-}}{lim} f(x) = \underset{x\rightarrow 3^{-}}{lim}\frac{x+2}{x^{2}-9} = \underset{x\rightarrow 3^{-}}{lim}\frac{x+2}{x+3}.\frac{1}{x-3} = -∞ vì \underset{x\rightarrow 3^{-}}{lim}\frac{x+2}{x+3} = \frac{5}{6} > 0 và \underset{x\rightarrow 3^{-}}{\lim} \frac{1}{x-3} = -∞.$

$\underset{x\rightarrow -3^{+}}{lim} f(x) =\underset{x\rightarrow -3^{+}}{lim}\frac{x+2}{x^{2}-9} = \underset{x\rightarrow -3^{+}}{lim}\frac{x+2}{x-3} . \frac{1}{x+3} = +∞ vì \underset{x\rightarrow -3^{+}}{lim}\frac{x+2}{x-3} = \frac{-1}{-6} = \frac{1}{6} > 0 và \underset{x\rightarrow -3^{+}}{lim}\frac{1}{x+3} = +∞.$ $\underset{x\rightarrow -3^{+}}{lim} f(x) =\underset{x\rightarrow -3^{+}}{lim}\frac{x+2}{x^{2}-9} = \underset{x\rightarrow -3^{+}}{lim}\frac{x+2}{x-3} . \frac{1}{x+3} = +∞ vì \underset{x\rightarrow -3^{+}}{lim}\frac{x+2}{x-3} = \frac{-1}{-6} = \frac{1}{6} > 0 và \underset{x\rightarrow -3^{+}}{lim}\frac{1}{x+3} = +∞.$

Bài 6 (trang 133 SGK Đại số 11): Tính:

Tính:

$\eqalign{ & a)\mathop {\lim }\limits_{x \to + \infty } ({x^4} - {x^2} + x - 1) \cr & b)\mathop {\lim }\limits_{x \to - \infty } ( - 2{x^3} + 3{x^2} - 5) \cr & c)\mathop {\lim }\limits_{x \to - \infty } (\sqrt {{x^2} - 2x + 5}) \cr & d)\mathop {\lim }\limits_{x \to + \infty } {{\sqrt {{x^2} + 1} + x} \over {5 - 2x}} \cr}$ $\eqalign{ & a)\mathop {\lim }\limits_{x \to + \infty } ({x^4} - {x^2} + x - 1) \cr & b)\mathop {\lim }\limits_{x \to - \infty } ( - 2{x^3} + 3{x^2} - 5) \cr & c)\mathop {\lim }\limits_{x \to - \infty } (\sqrt {{x^2} - 2x + 5}) \cr & d)\mathop {\lim }\limits_{x \to + \infty } {{\sqrt {{x^2} + 1} + x} \over {5 - 2x}} \cr}$

Lời giải:

$\begin{array}{l} a)\,\,\mathop {\lim }\limits_{x \to + \infty } \left( {{x^4} - {x^2} + x - 1} \right) \\= \mathop {\lim }\limits_{x \to + \infty } {x^4}\left( {1 - \frac{1}{{{x^2}}} + \frac{1}{{{x^3}}} - \frac{1}{{{x^4}}}} \right)\\ \mathop {\lim }\limits_{x \to + \infty } {x^4} = + \infty \\ \mathop {\lim }\limits_{x \to + \infty } \left( {1 - \frac{1}{{{x^2}}} + \frac{1}{{{x^3}}} - \frac{1}{{{x^4}}}} \right) = 1 > 0\\ \Rightarrow \mathop {\lim }\limits_{x \to + \infty } \left( {{x^4} - {x^2} + x - 1} \right) = + \infty \\\end{array}$ $\begin{array}{l} a)\,\,\mathop {\lim }\limits_{x \to + \infty } \left( {{x^4} - {x^2} + x - 1} \right) \\= \mathop {\lim }\limits_{x \to + \infty } {x^4}\left( {1 - \frac{1}{{{x^2}}} + \frac{1}{{{x^3}}} - \frac{1}{{{x^4}}}} \right)\\ \mathop {\lim }\limits_{x \to + \infty } {x^4} = + \infty \\ \mathop {\lim }\limits_{x \to + \infty } \left( {1 - \frac{1}{{{x^2}}} + \frac{1}{{{x^3}}} - \frac{1}{{{x^4}}}} \right) = 1 > 0\\ \Rightarrow \mathop {\lim }\limits_{x \to + \infty } \left( {{x^4} - {x^2} + x - 1} \right) = + \infty \\\end{array}$

$\begin{array}{l} b)\,\,\mathop {\lim }\limits_{x \to - \infty } \left( { - 2{x^3} + 3{x^2} - 5} \right) \\= \mathop {\lim }\limits_{x \to - \infty } {x^3}\left( { - 2 + \frac{1}{x} - \frac{5}{{{x^2}}}} \right)\\ \mathop {\lim }\limits_{x \to - \infty } {x^3} = - \infty \\ \mathop {\lim }\limits_{x \to - \infty } \left( { - 2 + \frac{1}{x} - \frac{5}{{{x^2}}}} \right) = - 2 < 0\\ \Leftrightarrow \mathop {\lim }\limits_{x \to - \infty } {x^3}\left( { - 2 + \frac{1}{x} - \frac{5}{{{x^2}}}} \right) = + \infty \\\end{array}$ $\begin{array}{l} b)\,\,\mathop {\lim }\limits_{x \to - \infty } \left( { - 2{x^3} + 3{x^2} - 5} \right) \\= \mathop {\lim }\limits_{x \to - \infty } {x^3}\left( { - 2 + \frac{1}{x} - \frac{5}{{{x^2}}}} \right)\\ \mathop {\lim }\limits_{x \to - \infty } {x^3} = - \infty \\ \mathop {\lim }\limits_{x \to - \infty } \left( { - 2 + \frac{1}{x} - \frac{5}{{{x^2}}}} \right) = - 2 < 0\\ \Leftrightarrow \mathop {\lim }\limits_{x \to - \infty } {x^3}\left( { - 2 + \frac{1}{x} - \frac{5}{{{x^2}}}} \right) = + \infty \\\end{array}$

$\begin{array}{l} c)\,\,\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - 2x + 5} } \right) = \mathop {\lim }\limits_{x \to - \infty } \left| x \right|\sqrt {1 - \frac{2}{x} + \frac{5}{{{x^2}}}} \\ = \mathop {\lim }\limits_{x \to - \infty } \left[ { - x\sqrt {1 - \frac{2}{x} + \frac{5}{{{x^2}}}} } \right]\\ \mathop {\lim }\limits_{x \to - \infty } \left( { - x} \right) = + \infty \\ \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {1 - \frac{2}{x} + \frac{5}{{{x^2}}}} } \right) = 1 > 0\\ \Rightarrow \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - 2x + 5} } \right) = + \infty \\\end{array}$ $\begin{array}{l} c)\,\,\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - 2x + 5} } \right) = \mathop {\lim }\limits_{x \to - \infty } \left| x \right|\sqrt {1 - \frac{2}{x} + \frac{5}{{{x^2}}}} \\ = \mathop {\lim }\limits_{x \to - \infty } \left[ { - x\sqrt {1 - \frac{2}{x} + \frac{5}{{{x^2}}}} } \right]\\ \mathop {\lim }\limits_{x \to - \infty } \left( { - x} \right) = + \infty \\ \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {1 - \frac{2}{x} + \frac{5}{{{x^2}}}} } \right) = 1 > 0\\ \Rightarrow \mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - 2x + 5} } \right) = + \infty \\\end{array}$

$\begin{array}{l} d)\,\,\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 1} + x}}{{5 - 2x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( {\sqrt {1 + \frac{1}{{{x^2}}}} + 1} \right)}}{{5 - 2x}}\\ = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {1 + \frac{1}{{{x^2}}}} + 1}}{{\frac{5}{x} - 2}} = \frac{{1 + 1}}{{ - 2}} = - 1 \end{array}$ $\begin{array}{l} d)\,\,\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {{x^2} + 1} + x}}{{5 - 2x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( {\sqrt {1 + \frac{1}{{{x^2}}}} + 1} \right)}}{{5 - 2x}}\\ = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {1 + \frac{1}{{{x^2}}}} + 1}}{{\frac{5}{x} - 2}} = \frac{{1 + 1}}{{ - 2}} = - 1 \end{array}$

Bài 7 (trang 133 SGK Đại số 11): Một thấu kính hội tụ có tiêu cự là f. Gọi d và d' lần lượt là khoảng cách từ một vật thật AB và ảnh A'B' của nó tới quang tâm O của thấu kính (hình dưới).

Lời giải:

a) Từ hệ thức $\frac{1}{d}+\frac{1}{d$ $\frac{1}{d}+\frac{1}{d'}=\frac{1}{f}.$

Suy ra $d' = φ(d) = \frac{fd}{d-f}$.

b)

$\begin{array}{l} + )\,\,\mathop {\lim }\limits_{d \to {f^ + }} \varphi \left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{fd}}{{d - f}}\\ \mathop {\lim }\limits_{d \to {f^ + }} \left( {fd} \right) = {f^2} > 0\\ \mathop {\lim }\limits_{d \to {f^ + }} \left( {d - f} \right) = 0;\,\,d \to {f^ + } \Rightarrow d > f \Rightarrow d - f > 0\\ \Rightarrow \mathop {\lim }\limits_{d \to {f^ + }} \varphi \left( d \right) = + \infty \end{array}$ $\begin{array}{l} + )\,\,\mathop {\lim }\limits_{d \to {f^ + }} \varphi \left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{fd}}{{d - f}}\\ \mathop {\lim }\limits_{d \to {f^ + }} \left( {fd} \right) = {f^2} > 0\\ \mathop {\lim }\limits_{d \to {f^ + }} \left( {d - f} \right) = 0;\,\,d \to {f^ + } \Rightarrow d > f \Rightarrow d - f > 0\\ \Rightarrow \mathop {\lim }\limits_{d \to {f^ + }} \varphi \left( d \right) = + \infty \end{array}$

Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn lớn hơn f thì ảnh của nó dần tới dương vô cực.

$\begin{array}{l} + )\,\,\mathop {\lim }\limits_{d \to {f^ - }} \varphi \left( d \right) = \mathop {\lim }\limits_{d \to {f^ - }} \frac{{fd}}{{d - f}}\\ \mathop {\lim }\limits_{d \to {f^ - }} \left( {fd} \right) = {f^2} > 0\\ \mathop {\lim }\limits_{d \to {f^ - }} \left( {d - f} \right) = 0;\,\,d \to {f^ - } \Rightarrow d < f \Rightarrow d - f < 0\\ \Rightarrow \mathop {\lim }\limits_{d \to {f^ - }} \varphi \left( d \right) = - \infty \end{array}$ $\begin{array}{l} + )\,\,\mathop {\lim }\limits_{d \to {f^ - }} \varphi \left( d \right) = \mathop {\lim }\limits_{d \to {f^ - }} \frac{{fd}}{{d - f}}\\ \mathop {\lim }\limits_{d \to {f^ - }} \left( {fd} \right) = {f^2} > 0\\ \mathop {\lim }\limits_{d \to {f^ - }} \left( {d - f} \right) = 0;\,\,d \to {f^ - } \Rightarrow d < f \Rightarrow d - f < 0\\ \Rightarrow \mathop {\lim }\limits_{d \to {f^ - }} \varphi \left( d \right) = - \infty \end{array}$

Ý nghĩa: Nếu vật thật AB tiến dần về tiêu điểm F sao cho d luôn nhỏ hơn f thì ảnh của nó dần tới âm vô sực.

$+) \underset{d\rightarrow +\infty }{lim} φ(d) =\underset{d\rightarrow +\infty }{lim}\frac{fd}{d-f} = \underset{d\rightarrow +\infty }{lim}\frac{f}{1-\frac{f}{d}} = f.$ $+) \underset{d\rightarrow +\infty }{lim} φ(d) =\underset{d\rightarrow +\infty }{lim}\frac{fd}{d-f} = \underset{d\rightarrow +\infty }{lim}\frac{f}{1-\frac{f}{d}} = f.$

Ý nghĩa: Nếu vật thật AB ở xa vô cực so với thấu kính thì ảnh của nó ở ngay trên tiêu diện ảnh (mặt phẳng qua tiêu điểm ảnh F' và vuông góc với trục chính).

------------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải bài tập Toán 11 bài 2: Giới hạn của hàm số. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Hóa học lớp 10, Giải bài tập Hóa học lớp 11, Hóa học lớp 12, Thi thpt Quốc gia môn Văn, Thi thpt Quốc gia môn Lịch sử, Thi thpt Quốc gia môn Địa lý, Thi thpt Quốc gia môn Toán, đề thi học kì 1 lớp 11, đề thi học kì 2 lớp 11 mà VnDoc tổng hợp và đăng tải.

Tải về

Chọn file muốn tải về: