VnDoc.com

11 đề ôn tập hè môn Toán lớp 11

Bài tập hè môn Toán lớp 11

Bài trước

Tải về

Bài sau

Lớp: Lớp 11

Môn: Toán

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Đề ôn tập hè môn Toán lớp 11

11 đề ôn tập hè môn Toán lớp 11 tổng hợp các đề kiểm tra ôn tập hè cho lớp 11 lên lớp 12, giúp các bạn củng cố lại kiến thức đã học, chuẩn bị sẵn sàng cho năm học mới hiệu quả hơn. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.

ÔN KIỂM TRA TOÁN 11

ĐỀ SỐ 1

Bài 1: Tìm tập xác định của hàm số

Bài 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: 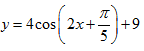11 đề ôn tập hè môn Toán lớp 11

Bài 3: Giải các phương trình sau:

a) sin2x - √3cos2x - √2 = 0.

b) 3cos²x + 2sin2x - 3sin²x = 0

c) 2cos2x + 1 = 0.

Bài 4: Cho tập A = {0; 1; 2; 3; 6; 7; 8}. Hỏi có bao nhiêu số tự nhiên chia hết cho 2 gồm có 6 chữ số khác nhau, trong đó mỗi chữ số lấy từ tập A.

Bài 5: Tìm số hạng độc lập với x trong khai triển: 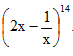11 đề ôn tập hè môn Toán lớp 11 .

Bài 6: Có hai hộp đựng bi. Hộp thứ nhất chứa 5 viên bi trắng và 4 viên bi vàng. Hộp thứ 2 chứa 6 viên bi trắng và 2 viên bi vàng. Lấy ngẫu nhiên mỗi hộp 1 viên bi. Tính xác suất để chọn được 2 viên bi khác màu.

Bài 7: Cho hình chóp S.ABCD có đáy ABCD là HBH. Gọi M, N lần lượt là trung điểm của SB, AB.

a) Tìm giao tuyến của (SAC) và (SBD); (SAD) và (SCB).

b) Gọi E thuộc SC và (SBD) sao cho SE = 2EC. Tìm giao điểm của đường thẳng AE và (SBD).

c) Gọi G₁, G₂ lần lượt là trọng tâm của ΔSBC và ΔABC. Chứng minh: G₁G₂ // (SAD).

ĐỀ SỐ 2

Bài 1: Tìm tập xác định của hàm số:

Bài 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: y = 1 - 5|sin3x|

Bài 3: Giải các phương trình:

11 đề ôn tập hè môn Toán lớp 11

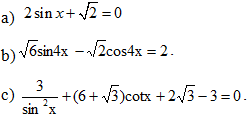
Bài 4: Tìm số nguyên dương n, biết rằng hệ số của x^n-2 trong 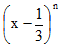11 đề ôn tập hè môn Toán lớp 11 bằng 70.

Bài 5: Cho một hộp kín chứa 8 viên bi đỏ, 7 viên bi xanh và 5 viên bi vàng.

a) Có bao nhiêu cách lấy 3 viên bi cùng màu.

b) Lấy ngẫu nhiên đồng thời 4 bi trong hộp trên. Tính xác suất để 4 bi lấy được có đủ 3 màu trong đó số bi đỏ là số lẻ.

Bài 6: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SB, CD, AD.

a) Tìm giao tuyến của (SAC) và (SBD); (SAD) và (SBC).

b) Tìm giao điểm E của SC và (MNP).

c) Chứng minh: NE // (SBP).

ĐỀ SỐ 3

Bài 1: Tìm tập xác định của hàm số: y = sin $\left(\frac{x+1}{x-1}\right)$ $\left(\frac{x+1}{x-1}\right)$

Bài 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: y = 3 $\sqrt{\cos x}$ $\sqrt{\cos x}$+2

Bài 3: Giải các phương trình:

a. $\sqrt{3}$ $\sqrt{3}$cosx + sinx = 1

b. cos2x + 3sinx - 2 = 0

c. (2cosx-1)(2sinx-1) = sin2x - sinx

Bài 4: Có bao nhiêu số tự nhiên gồm 4 chữ số được lập từ các chữ số 0; 1; 2; 3; 4; 5; 6.

Bài 5: Tìm số hạng không chứa x trong khai triển của biểu thức: (3x - 2/x³ )¹² , x≠0

Bài 6: Từ một hộp chứa 20 quả cầu, trong đó có 15 quả cầu màu xanh và 5 quả cầu màu đỏ. Lấy ngẫu nhiên đồng thời 2 quả cầu từ hộp trên. Tính xác suất để chọn được 2 quả cầu khác màu.

ĐỀ SỐ 4

Bài 1: Tìm tập xác định của hàm số: $y =\sqrt{\frac{1 - \sin x}{1 + \sin x}}$ $y =\sqrt{\frac{1 - \sin x}{1 + \sin x}}$

Bài 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: $y = \sqrt{5 - 4\sin^{2}x\cos^{2}x}$ $y = \sqrt{5 - 4\sin^{2}x\cos^{2}x}$

Bài 3: Giải các phương trình lượng giác sau:

a) $2\cos^{2}2x + 3\sin^{2}x = 2$ $2\cos^{2}2x + 3\sin^{2}x = 2$

b) $\sqrt{3}\cos x - \sin x - 2 = 0$ $\sqrt{3}\cos x - \sin x - 2 = 0$

c) $\cos4x + \sin3x.\cos x = \sin x.\cos3x$ $\cos4x + \sin3x.\cos x = \sin x.\cos3x$

Bài 4: Một hộp đựng 4 viên bi xanh, 3 viên bi đỏ và 2 viên bi vàng. Chọn ngẫu nhiên 2 viên bi.

Tính xác suất để chọn được 2 viên bi cùng màu.

Bài 5: Có bao nhiêu số chẵn gồm 6 chữ số khác nhau đôi một

Bài 6: Tìm hệ số của số hạng chứa x⁷ trong khai triển ( x + $\frac{2}{x^{3}}$ $\frac{2}{x^{3}}$)²⁷

Bài 7: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi K là trung điểm của SB, H là trung điểm của SD; và I là trọng tâm của tam giác ABD.

a. Chứng minh HK // (ABCD).

b. Cắt hình chóp bằng mp $(\alpha)$ $(\alpha)$qua I và song song với mp(SAD), mp $(\alpha)$ $(\alpha)$cắt các cạnh AB, CD, SC và

SB lần lượt tại M, N, P, Q. Vẽ thiết diện của mp $(\alpha)$ $(\alpha)$ và hình chóp. Hình tính của thiết diện?

c. Lấy điểm J trên cạnh SD sao cho DS = 3DJ. Chứng minh IJ // (SBC).

ĐỀ SỐ 5

Bài 1: Tìm tập xác định của hàm số: $y =\frac{2 - \sin x}{2\cos x - 1}$ $y =\frac{2 - \sin x}{2\cos x - 1}$

Bài 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: $y = 5 + \frac{1}{2}\cos x\sin x$ $y = 5 + \frac{1}{2}\cos x\sin x$

Câu 3: Giải các phương trình sau:

$a)2\cos^{2}x + 5\cos x - 3 = 0$ $a)2\cos^{2}x + 5\cos x - 3 = 0$

$b)\ \sqrt{3}\cos\left( x - \frac{\pi}{4} \right) + \sin\left( x - \frac{\pi}{4} \right) = 1\$ $b)\ \sqrt{3}\cos\left( x - \frac{\pi}{4} \right) + \sin\left( x - \frac{\pi}{4} \right) = 1\$

$c)\cos7x.\cos x = \cos5x.\cos3x$ $c)\cos7x.\cos x = \cos5x.\cos3x$

Câu 4: Tìm số hạng không chứa x trong khai triển $\left( \frac{4}{x} - 2x^{2} \right)^{15}\$ $\left( \frac{4}{x} - 2x^{2} \right)^{15}\$

Câu 5: a) Một hộp đựng 8 viên phấn trắng và 4 viên phấn đỏ. Hỏi có bao nhiêu cách để lấy được 3 viên phấn sao cho số viên phấn trắng nhiều hơn số viên phấn đỏ?

b) Gieo đồng thời hai con súc cân đối và đồng chất. Tính xác suất để tổng số chấm của hai mặt là một số chia hết cho 5.

Câu 6: Cho hình chóp SABCD, đáy ABCD là hình thang (AD // BC, AD > BC). Gọi M, N, K lần lượt là

trung điểm của cạnh SA, SD và AB.

a. Tìm giao tuyến của các cặp mặt phẳng: (SAC) và (SBD); (SAD) và (SBC).

b. Chứng minh đường thẳng SB song song mặt phẳng (CKM).

c. Tìm thiết diện của hình chóp SABCD cắt bởi mặt phẳng (α) qua điểm K và song song với mặt phẳng (CMN).

ĐỀ SỐ 6

Bài 1: Tìm tập xác định của hàm số: $y = \ \tan x\ \ + \frac{1}{sin2x}$ $y = \ \tan x\ \ + \frac{1}{sin2x}$

Bài 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: $y = \cos^{2}x +\cos2x$ $y = \cos^{2}x +\cos2x$

Câu 3. Giải các phương trình sau:

a) $\sin x + \sqrt{3}\cos x = 2$ $\sin x + \sqrt{3}\cos x = 2$

b) $\sin2x - 2\sin^{2}x = 2\cos2x$ $\sin2x - 2\sin^{2}x = 2\cos2x$

c) $3\sin^{2}x - \sin x\cos x - 2\cos^{2}x = 3$ $3\sin^{2}x - \sin x\cos x - 2\cos^{2}x = 3$

Câu 4. Tìm số hạng không chứa x trong khai triển $(2x^{3} - \frac{5}{x^{2}})^{20}$ $(2x^{3} - \frac{5}{x^{2}})^{20}$

Câu 5: Từ các chữ số 1; 2; 3; 4; 5 có thể lập được bao nhiêu số nguyên dương n có 5 chữ số đôi một khác nhau

Câu 6: Cho hình chóp SABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SA, BC, CD.

a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD)

b) Tìm giao tuyến của hai mặt phẳng (SAD) và (MOP)

c) Gọi K là điểm bất kỳ trên OM. Chứng minh KN//(SCD)

d) Mặt phẳng $(\alpha)$ $(\alpha)$qua N, song song với SA và CD. Tìm thiết diện của mặt phẳng $(\alpha)$ $(\alpha)$và hình chóp. Xác định hình tính thiết diện.

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

---------------------------------------------------------

Trên đây VnDoc.com vừa giới thiệu tới các bạn 11 đề ôn tập hè môn Toán lớp 11. Chắc hẳn qua bài viết bạn đọc đã nắm được những ý chính cũng như trau dồi được nội dung kiến thức của bài viết rồi đúng không ạ? Bài viết cho chúng ta thấy được các đề ôn tập hè cho môn Toán lớp 11. Mong rằng qua bài viết này các bạn có thể học tập tốt hơn môn Toán lớp 11. Để giúp các bạn có thêm nhiều tài liệu học tập hơn nữa, VnDoc.com mời các bạn cùng tham khảo thêm tài liệu học tập các môn được chúng tôi biên soạn và tổng hợp tại các mục Ngữ văn 11, Tiếng Anh 11, đề thi học kì 1 lớp 11, đề thi học kì 2 lớp 11...

Mời bạn đọc cùng tham gia nhóm Tài liệu học tập lớp 11 để có thêm tài liệu học tập nhé

Tải về

Chọn file muốn tải về: