VnDoc.com

Cách tính mốt mẫu số liệu ghép nhóm

Công thức tính mốt Toán 11

Bài trước

Tải về

Bài sau

Lớp: Lớp 11

Môn: Toán

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Tính mốt của mẫu số liệu ghép nhóm

A. Mốt của mẫu số liệu là gì?
B. Cách tìm mốt của mẫu số liệu ghép nhóm
C. Ví dụ minh họa tính mốt của mẫu số liệu ghép nhóm
D. Bài tập tự rèn luyện tính mốt mẫu số liệu ghép nhóm
- Đáp án chi tiết bài tập tự rèn luyện

Mốt (Mode) là giá trị xuất hiện nhiều nhất trong một dữ liệu, đặc biệt quan trọng khi phân tích các nhóm dữ liệu mẫu. Bài viết này sẽ hướng dẫn chi tiết công thức thu nhỏ của nhóm mẫu số liệu Toán lớp 11, giúp bạn dễ dàng áp dụng trong thống kê và phân tích dữ liệu thực tiễn.

A. Mốt của mẫu số liệu là gì?

Mốt của mẫu số liệu (tiếng Anh: mode) là giá trị xuất hiện nhiều nhất trong một tập hợp dữ liệu.

Định nghĩa đơn giản:

Mốt là giá trị có tần suất (số lần xuất hiện) cao nhất trong dãy số liệu.

Ví dụ:

Cho mẫu số liệu: 2, 3, 4, 2, 5, 2, 3

Số 2 xuất hiện 3 lần
Số 3 xuất hiện 2 lần
Các số khác xuất hiện ít hơn

Suy ra: Mốt = 2 (vì 2 là giá trị xuất hiện nhiều nhất)

B. Cách tìm mốt của mẫu số liệu ghép nhóm

Cho mẫu số liệu ghép nhóm:

Nhóm	$\left\lbrack a_{1};a_{2} \right)$	…	$\left\lbrack a_{i};a_{i + 1} \right)$	…	$\left\lbrack a_{k};a_{k + 1} \right)$
Tần số	$m_{1}$	…	$m_{i}$	…	$m_{k}$

Để tìm mốt của mẫu số liệu ghép nhóm, ta thực hiện theo các bước sau:

Bước 1: Xác định nhóm có tần số lớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm j: $\left\lbrack a_{j};a_{j + 1} \right)$ .

Bước 2: Mốt được xác định là:

$M_{0} = a_{j} + \frac{m_{j} - m_{j - 1}}{\left( m_{j} - m_{j - 1} \right) + \left( m_{j} - m_{j + 1} \right)}.h$

Trong đó $m_{j}$ là tần số của nhóm j (quy ước $m_{0} = m_{k + 1} = 0$ ) và h là độ dài của nhóm.

C. Ví dụ minh họa tính mốt của mẫu số liệu ghép nhóm

Ví dụ 1. Điểm kiểm tra khảo sát môn Tiếng Anh của lớp 11A được ghi trong bảng số liệu ghép nhóm như sau:

Điểm	[0; 20)	[20; 40)	[40; 60)	[60; 80)	[80; 100)
Số học sinh	5	9	12	10	6

Mốt của dữ liệu bằng bao nhiêu?

Hướng dẫn giải:

Mốt $M_{0}$ thuộc nhóm $\lbrack 40;60)$

Ta có:

Điểm	[0; 20)	[20; 40)	[40; 60)	[60; 80)	[80; 100)
Số học sinh	5	9	12	10	6
		$f_{0}$	$f_{1}$	$f_{2}$

$\Rightarrow l = 40;f_{0} = 9;f_{1} = 12;$ $f_{2} = 10;c = 60 - 40 = 20$

Khi đó mốt của dữ liệu được tính như sau:

$M_{0} = l + \frac{f_{1} - f_{0}}{\left( f_{1} - f_{0} \right) + \left( f_{1} - f_{2} \right)}.c$

$\Rightarrow M_{0} = 40 + \frac{12 - 9}{12 - 9 + 12 - 10}.20 = 52$

Ví dụ 2: Chị A lập bảng doanh thu bán hải sản của cửa hàng trong 20 ngày (đơn vị: triệu đồng) như sau:

Doanh thu	[5; 7)	[7; 9)	[9; 11)	[11; 13)	[13; 15)
Số ngày	2	7	7	3	1

Tìm mốt của mẫu dữ liệu ghép nhóm?

Hướng dẫn giải:

Có hai nhóm chứa mốt của mẫu số liệu trên đó là [7; 9) và [9; 11) do đó:

Xét nhóm [7; 9) ta có:

$M_{0} = 7 + \frac{7 - 2}{(7 - 2) + (7 - 7)}.(9 - 7) = 9$

Xét nhóm [9; 11) ta có:

$M'_{0} = 9 + \frac{7 - 7}{(7 - 7) + (7 - 3)}.(11 - 9) = 9$

Vậy mốt của mẫu số liệu ghép nhóm đã cho là 9.

Ví dụ 3. Tìm nhóm chứa mốt của mẫu dữ liệu dưới đây:

Nhóm dữ liệu	Tần số
(0; 15]	4
(15; 30]	12
(30; 45]	17
(45; 60]	7

Hướng dẫn giải

Nhóm chứa mốt là: (30; 45] vì có tần số cao nhất.

Ví dụ 4. Cho bảng thống kê khối lượng một số quả quýt (đơn vị: gam) trong B như sau:

Điểm trung bình	[80; 82)	[82; 84)	[84; 86)	[86; 88)	[88; 90)
Số quả thùng B	16	22	10	29	23

Xác định mốt của mẫu số liệu ở thùng B.

Hướng dẫn giải

Ta có:

Điểm trung bình	[80; 82)	[82; 84)	[84; 86)	[86; 88)	[88; 90)
Số quả thùng B	16	22	10	29	23
			$f_{0}$	$f_{1}$	$f_{2}$

$\Rightarrow l = 86;f_{0} = 10;f_{1} = 29;f_{2} = 23;c = 88 - 86 = 2$

Khi đó mốt của dữ liệu được tính như sau:

$M_{0} = l + \frac{f_{1} - f_{0}}{\left( f_{1} - f_{0} \right) + \left( f_{1} - f_{2} \right)}.c$

$\Rightarrow M_{0} = 86 + \frac{29 - 10}{29 - 10 + 29 - 23}.2 = 86,76$

D. Bài tập tự rèn luyện tính mốt mẫu số liệu ghép nhóm

Bài tập 1. Sản lượng xoài (tính bằng kg) được ghi lại trong bảng sau:

Sản lượng	[40; 50)	[50; 60)	[60; 70)	[70; 80)	[80; 90)	[90; 100)
Số cây	10	15	17	14	12	2

Tìm mốt của mẫu dữ liệu trên?

Bài tập 2. Chiều cao của một số học sinh nam được ghi trong bảng dữ liệu sau:

Chiều cao (cm)	Số học sinh
[95; 105)	9
[105; 115)	13
[115; 125)	26
[125; 135)	30
[135; 145)	12
[145; 155)	10

Tìm mốt của mẫu dữ liệu ghép nhóm. (Kết quả làm tròn đến chữ số thập phân thứ nhất).

Bài tập 3. Kết quả khảo sát cân nặng của 25 quả cam ở lô hàng A được cho ở bảng sau:

Cân nặng (g)	[150; 155)	[155; 160)	[160; 165)	[165; 170)	[170; 175)
Số quả cam ở lô hàng A	1	3	7	10	4

Nhóm chứa mốt là nhóm nào

A. $\lbrack 150;155)$ . B. $\lbrack 155;160)$ . C. $\lbrack 165;170)$ . D. $\lbrack 170;175)$ .

Bài tập 4. Người ta tiến hành phỏng vấn 30 người về một bộ phim mới chiếu trên truyền hình. Người điều tra yêu cầu cho điểm bộ phim (thang điểm là 100). Kết quả được trình bày trong bảng phân bố tần số ghép lớp sau đây:

Số điểm	[50; 60)	[60; 70)	[70; 80)	[80; 90)	[90; 100)
Số người	2	6	10	8	4

(VD) a) Ước lượng số trung bình của mẫu ghép là

(NB) b) Giá trị đại diện của nhóm $\lbrack 90;100)$ là 95.

(NB) c) Nhóm chứa mốt của mẫu số liệu trên là nhóm $\lbrack 80;90)$ .

(VD) d) Mốt của mẫu số liệu là

Bài tập 5. Bảng số liệu ghép nhóm sau cho biết chiều cao (cm) của 40 học sinh lớp 11A.

Khoảng chiều cao (cm)	[145; 1 50)	[150; 155)	[155; 160)	[160; 165)	[165; 170)
Số học sinh	7	13	6	8	6

Tìm mốt của mẫu số liệu ghép nhóm này, làm tròn đến hàng đơn vị.

Trả lời: …

Bài tập 6. Khảo sát thời gian tập thể dục của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Thời gian (phút)	[0; 20)	[20; 40)	[40; 60)	[60; 80)	[80; 100)
Số học sinh	5	9	12	10	6

Mốt của mẫu số liệu trên là

A. . B. . C. . D. .

Bài tập 7. Kết quả điểm thi của học sinh trong kì thi Tiếng Anh (thang điểm 100) được biểu diễn ở biểu đồ dưới đây:

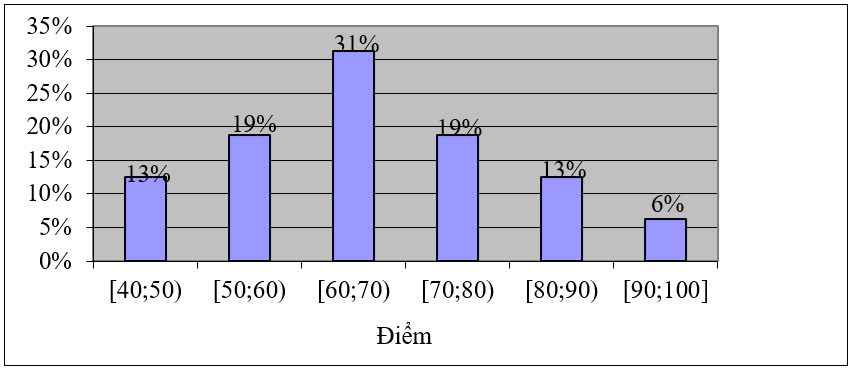
Hãy ước lượng mốt của mẫu số liệu trên?

A. . B. . C. . D. .

Bài tập 8. Khảo sát thời gian tự học bài ở nhà của một số em học sinh lớp 11 thu được mẫu ghép nhóm số lượng như sau:

Thời gian(phút)	[0; 30)	[30;60)	[60; 90)	[90; 120)	[120; 150)
Số học sinh	9	10	9	15	7

Mốt của số liệu ghép nhóm trên là

A. . B. . C. . D. .

Bài tập 9. Thời gian đề học sinh hoàn thành một câu hỏi thi được cho như sau:

Thời gian (phút)	[0,5; 10,5)	[10,5; 20,5)	[20,5; 30,5)	[30,5; 40,5)	[40,5; 50,5)
Số học sinh	2	10	6	4	3

Tìm mốt của mẫu số liệu ghép nhóm này.

A. . B. . C. . D. .

Bài tập 10. Thời gian truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:

Thời gian (phút)	[9,5; 12,5)	[12,5; 15,5)	[15,5; 18,5)	[18,5; 21,5)	[21,5; 24,5)
Số học sinh	3	12	15	24	2

Tìm mốt của mẫu số liệu ghép nhóm này.

A. . B. . C. . D. .

Đáp án chi tiết bài tập tự rèn luyện

Bài tập 1.

Quan sát bảng thống kê ta thấy tần số cao nhất là 17 nằm trong nhóm [60; 70).

Sản lượng	[40; 50)	[50; 60)	[60; 70)	[70; 80)	[80; 90)	[90; 100)
Số cây	10	15	17	14	12	2
		$f_{0}$	$f_{1}$	$f_{2}$

$\Rightarrow l = 60;f_{0} = 15;f_{1} = 17;f_{2} = 14;c = 70 - 60 = 10$

Khi đó ta tính mốt như sau:

$M_{0} = l + \frac{f_{1} - f_{0}}{2f_{1} - f_{0} - f_{2}}.c$

$\Rightarrow M_{0} = 60 + \frac{17 - 15}{2.17 - 15 - 14}.10 = 64$

Bài tập 2.

Ta có:

Chiều cao (cm)	Số học sinh
[95; 105)	9
[105; 115)	13
[115; 125)	26	$f_{0}$
[125; 135)	30	$f_{1}$
[135; 145)	12	$f_{2}$
[145; 155)	10

Ta có: Nhóm chứa mốt của mẫu dữ liệu ghép nhóm là: [125; 135)

Khi đó: $\left\{ \begin{matrix} l = 125;f_{0} = 26 \\ f_{1} = 30,f_{2} = 12;d = 135 - 125 = 10 \end{matrix} \right.$

Mốt của mẫu dữ liệu ghép nhóm là:

$M_{0} = l + \frac{f_{1} - f_{0}}{2f_{1} - f_{0} - f_{2}}.d$

$\Rightarrow M_{0} = 125 + \frac{30 - 26}{2.30 - 26 - 12}.10 = 126,8$

🔍 Để thuận tiện cho việc học tập và lưu trữ, mời bạn tải tài liệu tham khảo bên dưới.

------------------------------------------

Trên đây là hướng dẫn chi tiết cách tính mốt mẫu số liệu ghép nhóm giúp bạn hiểu rõ quy trình xác định giá trị xuất hiện nhiều nhất trong các nhóm dữ liệu phân lớp. Việc nắm vững phương pháp này không chỉ hỗ trợ phân tích thống kê chính xác hơn mà còn giúp đưa ra những nhận định khoa học, logic từ các bảng tần số đã được phân nhóm. Nếu bạn đang làm việc trong lĩnh vực nghiên cứu, giáo dục hoặc phân tích dữ liệu, hãy áp dụng công thức tính mốt vào thực tế để nâng cao hiệu quả xử lý thông tin. Đừng quên theo dõi thêm các bài viết khác trên VnDoc.com để cập nhật kiến thức thống kê hữu ích và chuẩn xác nhất!

Xem thử Tải về

Chọn file muốn tải về: