Toán 11 Bài 5: Khoảng cách
Lý thuyết Toán 11 Bài 5
VnDoc.com xin gửi tới bạn đọc bài viết Toán 11 Bài 5: Khoảng cách. Mời các bạn cùng tham khảo chi tiết.
I. Khoảng cách từ một điểm đến một đường thẳng, một mặt phẳng.
1. Khoảng cách từ một điểm đến một đường thẳng
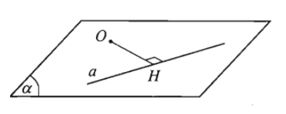
Cho điểm O và đường thẳng a. Trong mặt phẳng (O; a), gọi H là hình chiếu vuông góc của O lên a. Khi đó, khoảng cách giữa hai điểm O và H được gọi là khoảng cách từ điểm O đến đường thẳng a.
Kí hiệu: d(O; a).
Ví dụ 1. Cho hình lập phương ABCD. A'B'C'D' cạnh a. Tính khoảng cách từ B tới đường thẳng DB'.
Lời giải:
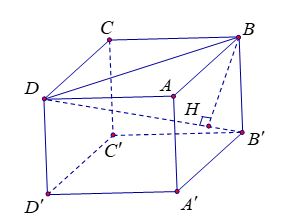
Từ giả thuyết ta suy ra: BD = 
\(\sqrt{BC^{2} + CD^{2} }\) = a\(\sqrt{2}\)
Gọi H là hình chiếu của B lên DB' ta có: BH = d (B, DB').
Xét tam giác BB'D vuông tại B ta có:
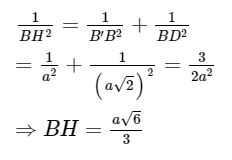
2. Khoảng cách từ một điểm đến một mặt phẳng
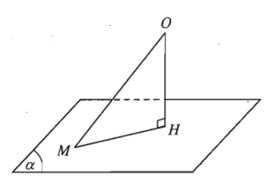
Cho điểm O và mặt phẳng (α). Gọi H là hình chiếu vuông góc của O lên mặt phẳng (α). Khi đó khoảng cách giữa hai điểm O và H được gọi là khoảng cách từ điểm O đến mặt phẳng (α) và được kí hiệu là d(O; (α)).
Ví dụ 2. Cho hình chóp S. ABC có SA⊥ (ABC), ∆ABC là tam giác đều cạnh a và tam giác SAB cân. Tính khoảng cách h từ điểm A đến mặt phẳng (SBC).
Lời giải:
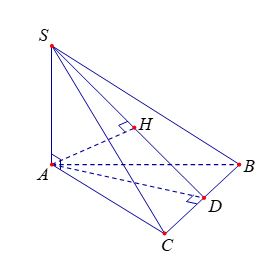
Gọi D là trung điểm BC. Do tam giác ABC đều nên AD ⊥BC (1).
Trong tam giác SAD, kẻ AH ⊥SD (2).
Do \(\left\{\begin{matrix} SA\perp (ABC) \Rightarrow SA\perp BC \\ AD \perp BC \\ SA \cap AD = (A) \end{matrix}\right.\) (3).
\(\Rightarrow BC \perp (SAD) \Rightarrow (SBC) \perp (SAD)\)
Từ (2) và (3), ta suy ra AH vuông góc với (SBC) nên d(A ; (SBC)) = AH.
Theo giả thiết, ta có SA = AB = a, AD = \(\frac{a\sqrt{3} }{2}\) (đường cao trong tam giác đều cạnh a).
Tam giác SAD vuông nên
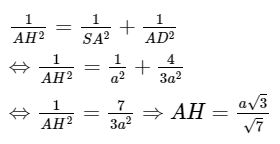
II. Khoảng cách giữa đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song.
1. Khoảng cách giữa đường thẳng và măt phẳng song song.
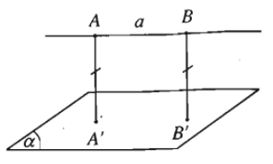
- Định nghĩa: Cho đường thẳng a song song với mặt phẳng (α). Khoảng cách giữa đường thẳng a và mặt phẳng (α) là khoảng cách từ một điểm bất kì thuộc a đến mặt phẳng (α).
Kí hiệu là d(a; (α)) .
2. Khoảng cách giữa hai mặt phẳng song song.
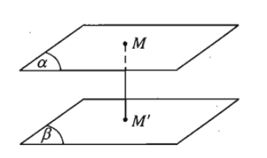
- Định nghĩa: Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này đến mặt phẳng kia.
- Kí hiệu: d((α); (β)).
Như vậy: d((α); (β)) = d(M; (β)) = d(M’; (α)).
III. Đường vuông góc chung và khoảng cách hai đường thẳng chéo nhau.
1. Định nghĩa.
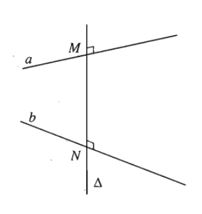
a) Đường thẳng ∆ cắt hai đường thẳng chéo nhau a, b và cùng vuông góc với mỗi đường thẳng ấy được gọi là đường vuông góc chung của a và b.
b) Nếu đường vuông góc chung ∆ cắt hai đường thẳng chéo nhau a, b lần lượt tại M; N thì độ dài đoạn thẳng MN gọi là khoảng cách giữa hai đường thẳng chéo nhau a và b.
2. Cách tìm đường vuông góc chung của hai đường thẳng chéo nhau.
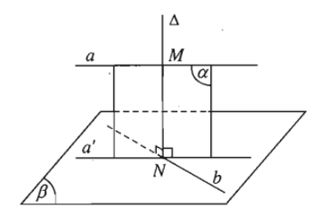
- Cho hai đường thẳng chéo nhau a và b. Gọi (β) là mặt phẳng chứa b và song song với a; a’ là hình chiếu vuông góc của a trên mặt phẳng (β).
Vì a// (β) nên a// a’. Do đó; a’ cắt b tại 1 điểm là N
Gọi (α) là mặt phẳng chứa a và a’; ∆ là đường thẳng đi qua N và vuông góc với (β). Khi đó, (α) vuông góc (β).
Như vậy.∆ nằm trong (α) nên cắt đường thẳng a tại M và cắt đường thẳng b tại N.Đồng thời, ∆ vuông góc với cả a và b.
Do đó, ∆ là đường vuông góc chung của a và b.
Ví dụ 3. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BC.
Lời giải :
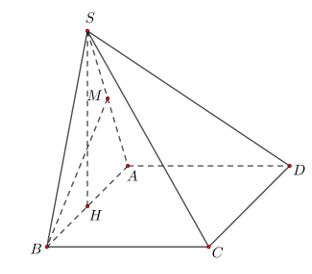
Do SAB ⊥ ABCD và BC ⊥ AB ⇒ BC ⊥ SAB.
Vì tam giác SAB đều nên gọi M là trung điểm của SA thì BM ⊥ SA nên BM là đoạn vuông góc chung của BC và SA.
Vậy dSA; BC = BM = \(\frac{a\sqrt{3} }{2}\).
3. Nhận xét
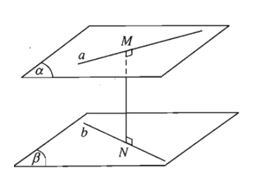
a) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó đến mặt phẳng song song với nó và chứa đường thẳng còn lại.
b) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.
Ví dụ 4. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, SA= a. Khoảng cách giữa hai đường thẳng SB và CD là
Lời giải :
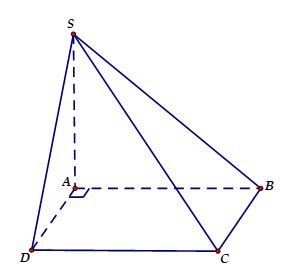
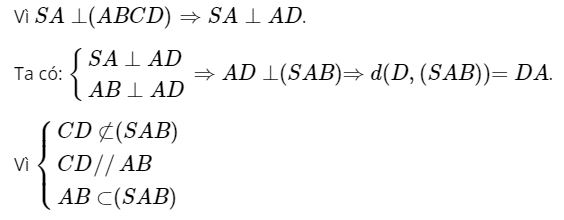
Suy ra: CD // (SAB) nên:
d(CD, SB) = d(CD, (SAB)) = d(D, (SAB)) = DA = a,
Trên đây VnDoc.com vừa gửi tới bạn đọc bài viết Toán 11 Bài 5: Khoảng cách. Hi vọng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán lớp 11. Mời các bạn cùng tham khảo thêm Lý thuyết Toán 11...
