Tứ diện đều

Bạn đang tìm hiểu về tứ diện đều trong hình học không gian? Đây là một trong những khối đa diện đặc biệt, thường xuyên xuất hiện trong chương trình Hình học lớp 11 cũng như các đề thi học kỳ, đề thi đại học. Bài viết “Tứ diện đều” dưới đây sẽ giúp bạn nắm rõ khái niệm, đặc điểm hình học, công thức tính toán liên quan và đặc biệt là tổng hợp tính chất tứ diện đều một cách đầy đủ, khoa học và dễ hiểu. Với hệ thống kiến thức chuẩn và ví dụ minh họa, bạn sẽ dễ dàng áp dụng vào bài tập và nâng cao tư duy hình học không gian của mình.

1. Tứ diện

• Tứ diện là hình có bốn đỉnh, thường được kí hiệu A, B, C, D. Bất kì điểm nào trong số các điểm trên được gọi là đỉnh, mặt tam giác đối diện với đỉnh đó được gọi là đáy. 
• Ví dụ: Chọn A là đỉnh thì (BCD) là mặt đáy.

2. Tứ diện đều

• Tứ diện đều là tứ diện có 4 mặt là tam giác đều.
• Tứ diện đều là một hình chóp tam giác đều.
• Hình chóp tam giác đều có thêm điều kiện cạnh bên bằng cạnh đáy là tứ diện đều.

Hình vẽ minh họa tứ diện đều

3. Tính chất tứ diện đều

- Tứ diện đều có các tính chất như sau:

• Bốn mặt xung quanh là các tam giác đều bằng nhau.
• Các mặt của tứ diện là những tam giác có ba góc đều nhọn.
• Tổng các góc tại một đỉnh bất kì của tứ diện là 180⁰.
• Hai cặp cạnh đối diện trong một tứ diện có độ dài bằng nhau.
• Tất cả các mặt của tứ diện đều tương đương nhau.
• Bốn đường cao của tứ diện đều có độ dài bằng nhau.
• Tâm của các mặt cầu nội tiếp và ngoại tiếp nhau, trùng với tâm của tứ diện.
• Hình hộp ngoại tiếp tứ diện là hình hộp chữ nhật.
• Các góc phẳng nhị diện ứng với mỗi cặp cạnh đối diện của tứ diện bằng nhau.
• Đoạn thẳng nối trung điểm của các cạnh đối diện là một đường thẳng đứng vuông góc của cả hai cạnh đó.
• Một tứ diện có ba trục đối xứng.
• Tổng các cos của các góc phẳng nhị diện chứa cùng một mặt của tứ diện bằng 1.

4. Cách vẽ tứ diện đều

Để giải các bài toán hình học không gian liên quan đến tứ diện đều, việc vẽ chính xác hình tứ diện là bước khởi đầu rất quan trọng. Một hình tứ diện đều được xây dựng như sau:

Bước 1: Xác định hình chóp tam giác đều

Hình tứ diện đều có thể được hình dung như một hình chóp tam giác đều với đỉnh A và mặt đáy là tam giác BCD.

Bước 2: Vẽ mặt đáy tam giác BCD

Bắt đầu bằng cách vẽ tam giác BCD, đảm bảo rằng đây là một tam giác đều.

Bước 3: Tìm trọng tâm của tam giác đáy

Dựng các đường trung tuyến của tam giác BCD để xác định trọng tâm G, điểm giao của các đường trung tuyến.

Bước 4: Dựng đường cao của hình

Từ trọng tâm G của tam giác BCD, dựng một đường thẳng vuông góc với mặt phẳng chứa tam giác BCD. Đây chính là đường cao của hình tứ diện.

Bước 5: Định vị đỉnh A

Chọn đỉnh A trên đường cao vừa dựng sao cho khoảng cách từ A đến mặt phẳng đáy BCD đảm bảo tứ diện đều (thường dựa vào bài toán hoặc mô hình).

Bước 6: Hoàn thiện các cạnh

Nối đỉnh A với các đỉnh B, C, D của tam giác đáy. Bạn sẽ thu được một hình tứ diện đều hoàn chỉnh.

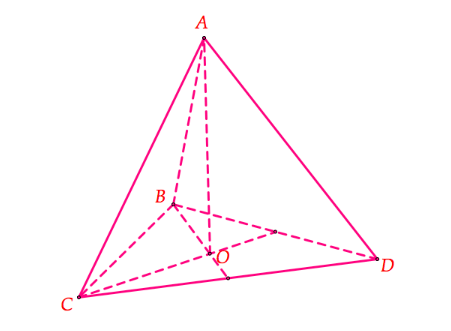
5. Hình tứ diện đều có bao nhiêu mặt phẳng đối xứng

Chúng ta xem hình sau thì sẽ hiểu rõ về 6 mặt phẳng đối diện nhau của hình tứ diện đều:

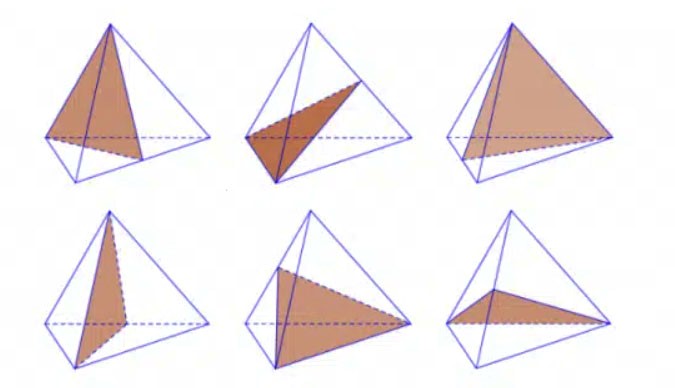
5. Thể tích tứ diện đều

- Một tứ diện đều sẽ có 6 cạnh bằng nhau và 4 mặt tam giác đều sẽ có các công thức tính thể tích tứ diện

Thể tích tứ diện ABCD

Thể tích của một khối tứ diện bằng một phần ba tích số của diện tích mặt đáy và chiều cao của khối tứ diện tương ứng:

\(V=\dfrac{1}{3}.S_{BCD}.AH\)
Thể tích tứ diện đều tam giác S.ABC

Thể tích của một khối chóp bằng một phần ba tích số của diện tích mặt đáy và chiều cao của khối chóp đó:

\(V=\dfrac{1}{3}.B.h\)

6. Công thức tính nhanh thể tích tứ diện đều cạnh a

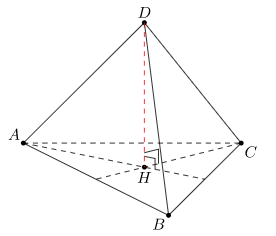
Cho tứ diện đều ABCD cạnh a. từ A kẻ AH là đường cao của hình chóp A.BCD, H thuộc (BCD) thì H sẽ là tâm của tam giác đều BCD. Suy ra 

• Chiều cao của hình chóp A.BCD đều cạnh a là _{\(h = AH=\frac{a\sqrt{6}}{3}\)}
• Thể tích khối tứ diện đều cạnh a là _{\(V=\frac{a^3\sqrt{2}}{12}\)}

Chứng minh 

Hình vẽ minh họa

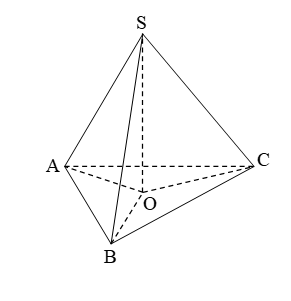
Gọi tứ diện \(ABCD\) đều cạnh \(a\).

Gọi \(H\) là hình chiếu của \(A\) lên \((BCD)\).

Ta có: \(BH = \frac{a\sqrt{3}}{3}\)

\(\Rightarrow AH = \sqrt{AB^{2} - BH^{2}} = \frac{a\sqrt{6}}{3}\)

\(S_{\Delta BCD} = \frac{a^{2}\sqrt{3}}{4}\) \(\Rightarrow V_{ABCD} = \frac{a^{3}\sqrt{2}}{12}\).

Ví dụ 1. Giả sử \(V\) là thể tích khối tứ diện đều \(ABCD\). Trung điểm tất cả các cạnh của tứ diện tạo thành một đa diện có thể tích \(V'\). Tỉ số \(\frac{V'}{V}\) bằng bao nhiêu?

(Kết quả được ghi dưới dạng phân số tối giản a/b)

Hướng dẫn giải:

Hình vẽ minh họa

Giả sử tứ diện đều cạnh bằng a

Hình đa diện cần tính có được bằng cách cắt 4 góc tứ diện

Mỗi góc cũng là một tứ diện đều có cạnh bằng \(\frac{a}{2}\)

Do đó thể tích phần cắt bỏ là \(V'' = 4.\frac{V}{8} = \frac{V}{2}\)

(Vì tứ diện cạnh giảm một nưả thì thể tích giảm \(\left( \frac{1}{2} \right)^{3} = \frac{1}{8}\)

Vậy \(V' = \frac{V}{2} \Rightarrow \frac{V'}{V} = \frac{1}{2}\)

Ví dụ 2. Tính thể tích khối tứ diện đều \(A.BCD\), biết \(AB = 3\)?

Hướng dẫn giải:

Hình vẽ minh họa

Gọi E là trung điểm của CD, H là trọng tâm giác giác BCD \(SH\bot(ABC)\)

Tam giác BCD đều cạnh bằng 5

\(\Rightarrow BE = \sqrt{3^{2} - \left( \frac{3}{2} \right)^{2}} = \frac{3\sqrt{3}}{2} \Rightarrow BH = \sqrt{3}\)

Tam giác ABH vuông tại H nên

\(\Rightarrow AH = \sqrt{AB^{2} - BH^{2}} = \sqrt{3^{2} - \left( \sqrt{3} \right)^{2}} = \sqrt{6}\)

\(\Rightarrow S_{ABCD} = \frac{1}{2}BE.CD = \frac{1}{2}.\frac{3\sqrt{3}}{2}.3 = \frac{9\sqrt{3}}{4}\)

Vậy thể tích khối chóp tam giác là: \(V = \frac{1}{3}.\frac{9\sqrt{3}}{4}.\sqrt{6} = \frac{9\sqrt{2}}{4}cm^{3}\)

Ví dụ 3. Cho tứ diện đều \(ABCD\) cạnh bằng \(a\), \(M\) là trung điểm của cạnh \(BC\). Gọi \(\alpha\) là góc giữa hai đường thẳng \(AB\) và \(DM\). Khi đó \(\cos\alpha\) bằng bao nhiêu?

Hướng dẫn giải:

Hình vẽ minh họa

Gọi N là trung điểm của BC

=> MN là đường trung bình tam giác ABC

\(\Rightarrow \left\{ \begin{matrix} MN//AB \\ MN = \frac{1}{2}AB \\ \end{matrix} \right.\)

Vì tam giác BCD và tam giác ACD là các tam giác đều cạnh a

\(\Rightarrow MD = ND = \frac{a\sqrt{3}}{2}\)

Vì \(MN//AB \Rightarrow \alpha = (AB,DM) = (MN,DM)\)

Xét tam giác MND ta có:

\(\cos\widehat{NMD} = \frac{MN^{2} + MD^{2} - ND^{2}}{2MN.MD}\)\(= \frac{\left( \frac{a}{2} \right)^{2} + \left( \frac{a\sqrt{3}}{2} \right)^{2} - \left( \frac{a\sqrt{3}}{2} \right)^{2}}{2.\frac{a}{2}.\frac{a\sqrt{3}}{2}} = \frac{\sqrt{3}}{6} > 0\)

\(\Rightarrow \widehat{NMD} < 90^{0} \Rightarrow (MN,DM) = \widehat{NMD}\)

\(\Rightarrow \cos\alpha = \cos\widehat{NMD} = \frac{\sqrt{3}}{6}\)

7. Ứng dụng thực tế của tứ diện đều

Tứ diện đều là một hình khối đa diện có tính đối xứng cao, do đó nó có nhiều ứng dụng trong thực tiễn, đặc biệt là trong các lĩnh vực khoa học, kỹ thuật và thiết kế. Dưới đây là một số ứng dụng cụ thể:

- Trong Hóa học:

• Cấu trúc phân tử: Nhiều phân tử hóa học có cấu trúc tứ diện đều, chẳng hạn như phân tử metan (CH4). Cấu trúc này giúp phân tử đạt được độ bền vững cao do sự phân bố đều của các liên kết.
• Tinh thể học: Một số tinh thể có cấu trúc mạng lưới tứ diện đều, điều này ảnh hưởng đến tính chất vật lý và hóa học của vật liệu.

- Trong Kiến trúc và Thiết kế:

• Thiết kế mái vòm: Cấu trúc tứ diện đều có thể được sử dụng để thiết kế các mái vòm có độ bền cao và khả năng chịu lực tốt.
• Thiết kế đồ chơi và trò chơi: Hình dạng tứ diện đều được sử dụng trong thiết kế đồ chơi và trò chơi, chẳng hạn như rubik tứ diện.
• Thiết kế các công trình có tính thẩm mỹ cao: tính đối xứng của tứ diện đều được áp dụng vào các công trình kiến trúc hoặc vật dụng để tạo ra tính thẩm mỹ.

- Trong Toán học và Khoa học máy tính:

• Hình học không gian: Tứ diện đều là một đối tượng nghiên cứu quan trọng trong hình học không gian, giúp chúng ta hiểu rõ hơn về các khái niệm như thể tích, diện tích và tính đối xứng.
• Đồ họa máy tính: Tứ diện đều được sử dụng trong đồ họa máy tính để tạo ra các mô hình 3D và các hiệu ứng đặc biệt.

- Trong Vật liệu học:

• Vật liệu nano: Cấu trúc tứ diện đều được sử dụng trong việc thiết kế và chế tạo các vật liệu nano có tính chất đặc biệt.
• Vật liệu xây dựng: Một số vật liệu xây dựng có cấu trúc tinh thể tứ diện đều, điều này ảnh hưởng đến độ bền và khả năng chịu lực của vật liệu.

8. Bài tập tính thể tích khối tứ diện đều

Câu 1: Khối chóp tứ diện đều cạnh a có thể tích bằng:

\(A. \frac{a^3}{3}\)	\(B.\frac{a^3\sqrt{6} }{12}\)
\(C.\frac{a^3\sqrt{2} }{12}\)	\(D.\frac{a^3\sqrt{3} }{12}\)

Câu 2: Số mặt phẳng đối xứng của hình tứ diện đều là:

A. 4 mặt phẳng	B. 6 mặt phẳng
C. 8 mặt phẳng	D. 10 mặt phẳng

Câu 3: Trung điểm các cạnh của một tứ diện đều tạo thành:

A. Các đỉnh của một hình hai mươi mặt đều.

B. Các đỉnh của một hình mười hai mặt đều.

C. Các đỉnh của một hình bát diện đều.

D. Các đỉnh của một hình tứ diện.

Câu 4: Cho khối chóp tam giác đều S. ABC có cạnh đáy bằng a, cạnh bên gấp 2 lần cạnh đáy. Tính theo a thể tích V của khối chóp S.ABC.

\(A.V=\frac{\sqrt{11}a^3 }{4}\)	\(B.V=\frac{\sqrt{13}a^3 }{12}\)
\(C.V=\frac{\sqrt{11}a^3 }{12}\)	\(D.V=\frac{\sqrt{11}a^3 }{6}\)

Câu 5: Cho hình chóp tam giác đều S.ABC có cạnh đáy a và cạnh bên bằng _{\(\frac{a\sqrt{21} }{6}\). Tính thể tích khối chóp S.ABC.}

\(A.V=\frac{\sqrt{3}a^3 }{6}\)	\(B.V=\frac{\sqrt{3}a^3 }{8}\)
\(C.V=\frac{\sqrt{3}a^3 }{12}\)	\(D.V=\frac{\sqrt{3}a^3 }{24}\)

Câu 6: Cho tứ diện đều ABCD có thể tích bằng 12 và G là trọng tâm của tam giác BCD. tính thể tích của khối chóp A.GBC.

\(A.V=4\)	\(B.V=5\)
\(C.V=3\)	\(D.V=6\)

Câu 7: Cho tứ diện đều ABCD có canh 2a. Tính thể tích khối tứ diện ABCD theo a

\(A.V=\frac{1}{3}a^3\)	\(B.V=\frac{\sqrt{2}a^3 }{3}\)
\(A.V=\frac{2\sqrt{2}a^3 }{3}\)	\(A.V=\frac{2a^3 }{3}\)

Câu 8: Cho tứ diện đều ABCD có canh _{\(\sqrt{2} a\)}. Tính thể tích khối tứ diện ABCD theo a

\(A.V=\frac{2a^3}{3}\)	\(B.\frac{\sqrt{2}a^3}{3}\)
\(C.V=\frac{a^3}{3}\)	\(D.V=\frac{4a^3}{3}\)

Câu 9: Cho tứ diện đều ABCD có thể tích bằng 1. Tìm độ dài các cạnh của tứ diện

A. \(2\sqrt{3}\)

B. \(3\sqrt{2}\)

C. \(6\sqrt{2}\)

D. \(\sqrt[3]{6\sqrt{2}}\)

Bài tập tự luận

Bài 1: Hãy tính thể tích khối tứ diện đều ABCD biết:

a) cạnh AB = 4 cm

b) cạnh CD = 6 cm

c) cạnh BD = 3 cm

Hướng dẫn giải

a) Vì là tứ diện đều nên các cạnh có độ dài bằng nhau: BC = CD = DA = BD = AC = AB = 4 cm nên thể tích là

Cho hình tứ diện đều ABCD cạnh a = 5 cm. Hỏi thế tích bằng bao nhiêub) Vì là tứ diện đều nên AB = BC = DA = BD = AC = CD = 6 cm nên thể tích là

c) Vì là tứ diện đều nên AB = BC = CD = DA = AC = BD = 3 cm nên thể tích

Bài 2: Cho hình chóp đều S.ABCD (đáy là hình vuông), đường SA vuông góc với mặt phẳng (ABCD). Xác định hình chóp này có mặt đối xứng nào.

Lời giải:

Ta có: BD vuông góc với AC, BD vuông góc với SA. Suy ra, BD vuông góc với (SAC). Từ đó ta suy ra (SAC) là mặt phẳng trung trực của BD. Ta kết luận rằng, (SAC) là mặt đối xứng của hình chóp và đây là mặt phẳng duy nhất.

Bài 3: Tìm số mặt phẳng đối xứng của hình tứ diện đều.

Lời giải: Các mặt phẳng đối xứng của hình tứ diện đều là các mặt phẳng chứa một cạnh và qua trung điểm cạnh đối diện. Vì vậy, hình tứ diện đều sẽ có 6 mặt phẳng đối xứng.

Bài 4: Cho tứ diện đều ABCD cạnh a. Tính góc giữa AB và CD?

Bài 5: Cho ABCD là tứ diện đều, cạnh a. Kéo dài BC 1 đoạn CE = a. Kéo dài BD 1 đoạn DF = a. M là trung điểm của AB.

a. Tìm thiết diện của tứ diện với mp(MEF).

b. Tính diện tích của thiết diện theo a.

----------------------------------------------------------------

Qua bài viết này, bạn đã có cái nhìn toàn diện về tứ diện đều cùng những tính chất tứ diện đều quan trọng giúp giải nhanh các dạng bài tập từ cơ bản đến nâng cao. Việc nắm chắc kiến thức này không chỉ giúp bạn học tốt hình học không gian mà còn tăng khả năng xử lý các bài toán ứng dụng trong đề thi.
Hãy lưu lại bài viết này để ôn tập thường xuyên, chia sẻ cho bạn bè đang học cùng để cùng nhau nâng cao kỹ năng. Đừng quên khám phá thêm nhiều chuyên đề hình học khác như lăng trụ, hình chóp hay quan hệ song song – vuông góc để xây dựng nền tảng vững chắc. Chúc bạn học tốt và chinh phục mọi đề toán một cách dễ dàng!