Cách bấm máy tính đạo hàm
Cách tính đạo hàm bằng máy tính Casio Toán 11
Bấm máy tính Casio tính đạo hàm Toán lớp 11 vừa được VnDoc.com sưu tầm và xin gửi tới bạn đọc cùng tham khảo. Mời các bạn cùng theo dõi bài viết dưới đây nhé.
- Trong giải tích toán học, đạo hàm là một hàm mô tả sự biến thiên tại một điểm. Nói cách khác, đạo hàm là tỷ số giữa số gia và hàm số tại một điểm x0. Độ lớn của biến thể và hướng của biến thể đại diện cho giá trị của đạo hàm. Tuy nhiên, theo một định nghĩa khác của Wikipedia thì đạo hàm được hiểu là sự biến thiên lên xuống của hàm số tại điểm thay đổi. Ngoài ra trong Vật lý đạo hàm được coi là vận tốc tức thời khi một vật đang chuyển động.
A. Cách bấm máy tính đạo hàm cấp 1
Bấm máy tính cầm tay tính đạo hàm cấp 1
- Bước 1: Bấm tổ hợp phím
 +
+ 
- Bước 2: Nhập hàm số tại điểm x0 và ẩn bằng.
Ví dụ 1: Cho hàm số ![]() \(y = \sqrt {4x - 1}\). Tính đạo hàm của hàm số tại x = 2
\(y = \sqrt {4x - 1}\). Tính đạo hàm của hàm số tại x = 2
Hướng dẫn giải
Bước 1: Bấm tổ hợp phím ![]() +
+![]() ta được:
ta được: 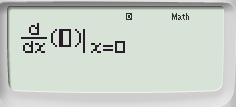
Bước 2: Nhập hàm số ![]() \(y = \sqrt {4x - 1}\) và x = 2 ta được
\(y = \sqrt {4x - 1}\) và x = 2 ta được 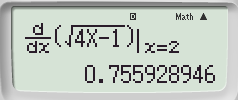
Nhấn “=” ta được kết quả cần tìm: 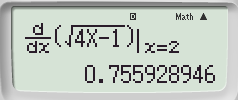
B. Cách bấm máy tính đạo hàm cấp 2
Công thức tính đạo hàm cấp 2:
![]() \(y''\left( {{x_0}} \right) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y'}}{{\Delta x}} = \frac{{y'\left( {{x_0} + 0,000001} \right) - y'\left( {{x_0}} \right)}}{{0,000001}}\)
\(y''\left( {{x_0}} \right) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y'}}{{\Delta x}} = \frac{{y'\left( {{x_0} + 0,000001} \right) - y'\left( {{x_0}} \right)}}{{0,000001}}\)
- Bước 1: Tính đạo hàm cấp 1 tại x = x0
- Bước 2: Tính đạo hàm cấp 1 tại x = x0 + 0,000001
- Nhập vào máy tính
 \(\frac{{Ans - \Pr eAns}}{x}\) rồi nhấn "="
\(\frac{{Ans - \Pr eAns}}{x}\) rồi nhấn "="
Ví dụ 2: Tính giá trị gần đúng đạo hàm cấp hai của hàm số ![]() \(y = 4{x^3} + \sqrt {x + 1}\) tại x0 = 3
\(y = 4{x^3} + \sqrt {x + 1}\) tại x0 = 3
Hướng dẫn giải
Bước 1: Tính đạo hàm cấp 1 của hàm số tại tại x0 = 3
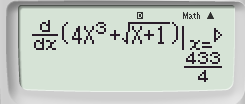
Bước 2: Lưu kết quả vừa tìm được vào hàm A
Bấm tổ hợp phím ![]() +
+ ![]() +
+ ![]() ta được:
ta được: 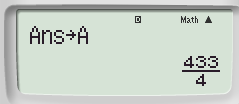
Bước 3: Tính đạo hàm cấp 1 của hàm số tại tại x0 = 3 + 0.000001
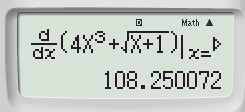
Lưu kết quả vào hàm B
Bấm tổ hợp phím ![]() +
+ ![]() +
+ ![]() ta được:
ta được: 
Bước 4: Áp dụng công thức đạo hàm cấp 2 ta có: ![]() \(y'' = \frac{{y'\left( {3 + 0.00001} \right) - y'\left( 3 \right)}}{{0.000001}}\)
\(y'' = \frac{{y'\left( {3 + 0.00001} \right) - y'\left( 3 \right)}}{{0.000001}}\)
Ta được kết quả: 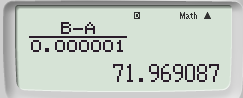
Dự đoán công thức đạo hàm bậc n:
- Bước 1: Tính đạo hàm cấp 1, đạo hàm cấp 2, đạo hàm cấp 3
- Bước 2: Tìm quy luật về dấu, về hệ số, về biến số, về số mũ rồi rút ra công thức tổng quát
C. Tính đạo hàm của hàm số bằng máy tính cầm tay
Bài tập 1: Tính đạo hàm của hàm số ![]() \(y =
\frac{x + 1}{4^{x}}\)?
\(y =
\frac{x + 1}{4^{x}}\)?
A.  \(y' = \frac{1 - 2(x +
1)ln2}{2^{2x}}\) \(y' = \frac{1 - 2(x +
1)ln2}{2^{2x}}\) |
B.  \(y' = \frac{1 + 2(x +
1)ln2}{2^{2x}}\) \(y' = \frac{1 + 2(x +
1)ln2}{2^{2x}}\) |
C.  \(y' = \frac{1 - 2(x +
1)ln2}{2^{x^{2}}}\) \(y' = \frac{1 - 2(x +
1)ln2}{2^{x^{2}}}\) |
D.  \(y' = \frac{1 + 2(x +
1)ln2}{2^{x^{2}}}\) \(y' = \frac{1 + 2(x +
1)ln2}{2^{x^{2}}}\) |
Hướng dẫn giải
Ta sẽ tính đạo hàm tại điểm bất kì ví dụ chọn x = 0,5 rồi tính đạo hàm của hàm số tại X = 0,5
Bước 1: Nhấn tổ hợp phím SHIFT ⟶ ![]()
Bước 2: Nhập vào máy tính biểu thức ta được
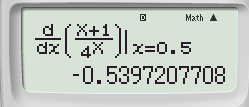
Bước 3: Nhấn tổ hợp phím SHIFT ⟶ RCL ⟶ (-) để gán kết quả vào biến A ta được:

Bước 4: Lấy A trừ đi kết quả tình các giá trị ở các đáp án nếu ra kết quả bằng 0 thì chọn đáp án đó
Ví dụ ta thử với đáp án A như sau:
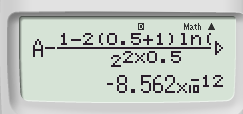
Vì kết quả này xấp xỉ bằng 0 nên ta chọn đáp án A
Chú ý: Nếu chưa ra kết quả bằng 0 thì ta thay tiếp tục vào các đáp án còn lại, khi nào đạt kết quả bằng 0 thì chọn.
Bài tập 2: Đạo hàm cấp 2 của hàm số ![]() \(y =
x^{4} - \sqrt{x}\) tại điểm có hoành độ x0 = 2 gần số giá trị nào nhất trong các giá trị sau:
\(y =
x^{4} - \sqrt{x}\) tại điểm có hoành độ x0 = 2 gần số giá trị nào nhất trong các giá trị sau:
| A. 7 | B. 19 | C. 25 | D. 48 |
Hướng dẫn giải
Bước 1: Nhấn tổ hợp phím SHIFT ⟶ ![]()
Bước 2: Tính đạo hàm cấp 1 tại điểm x = 2
Nhập vào máy tính biểu thức ta được
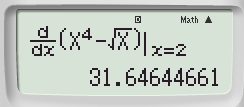
Bước 3: Tính đạo hàm cấp 1 tại điểm x = 2 + 0,000001 ta được:
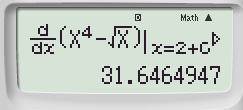
Bước 4: Áp dụng công thức  \(y''\left( x_{0} \right) = \lim_{\Delta x
\rightarrow 0}\frac{\Delta y'}{\Delta x} = \frac{y'\left( x_{0}
+ 0,000001 \right) - y'\left( x_{0} \right)}{0,000001}\) nhờ
\(y''\left( x_{0} \right) = \lim_{\Delta x
\rightarrow 0}\frac{\Delta y'}{\Delta x} = \frac{y'\left( x_{0}
+ 0,000001 \right) - y'\left( x_{0} \right)}{0,000001}\) nhờ ![]() \(\frac{Ans - \Pr eAns}{X}\) ⟶ = ta được
\(\frac{Ans - \Pr eAns}{X}\) ⟶ = ta được
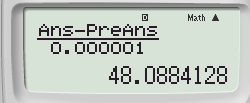
Vậy y’’(2) xấp xỉ 48
Chọn đáp án D
D. Bài tập tính đạo hàm bằng máy tính casio
Bài 1. Cho hàm số ![]() \(y = f(x) = \frac{3x +5}{ 1 + 2x}\). Mệnh đề nào dưới đây là mệnh đề sau?
\(y = f(x) = \frac{3x +5}{ 1 + 2x}\). Mệnh đề nào dưới đây là mệnh đề sau?
A. \(f'(x) = \frac{7}{(2x +
1)^{2}}\) \(f'(x) = \frac{7}{(2x +
1)^{2}}\) |
B. \(f'(x) = \frac{1}{(2x +
1)^{2}}\) \(f'(x) = \frac{1}{(2x +
1)^{2}}\) |
C.  \(f'(x) = \frac{- 13}{(2x +
1)^{2}}\) \(f'(x) = \frac{- 13}{(2x +
1)^{2}}\) |
D. \(f'(x) = \frac{13}{(2x +
1)^{2}}\) \(f'(x) = \frac{13}{(2x +
1)^{2}}\) |
Bài 2. Đạo hàm của hàm số ![]() \(y = \frac{1}{2}
- \frac{1}{3}x + x^{2} - 0,25x^{4}\) là:
\(y = \frac{1}{2}
- \frac{1}{3}x + x^{2} - 0,25x^{4}\) là:
A.  \(y' = - \frac{1}{3} + 2x -
2x^{3}\) \(y' = - \frac{1}{3} + 2x -
2x^{3}\) |
B. |
C.  \(y' = \frac{1}{3} + x -
2x^{3}\) \(y' = \frac{1}{3} + x -
2x^{3}\) |
D.  \(y' = - \frac{1}{3} + 2x -
x^{3}\) \(y' = - \frac{1}{3} + 2x -
x^{3}\) |
Bài 3. Tính đạo hàm của hàm số ![]() \(f(x) =
\left( x^{3} - 2x^{2} \right)^{2}\)?
\(f(x) =
\left( x^{3} - 2x^{2} \right)^{2}\)?
A. \(f'(x) = 6x^{5} - 20x^{4} +
16x^{3}\) \(f'(x) = 6x^{5} - 20x^{4} +
16x^{3}\) |
B. \(f'(x) = 6x^{5} +
16x^{3}\) \(f'(x) = 6x^{5} +
16x^{3}\) |
C. \(f'(x) = 6x^{5} - 20x^{4} +
4x^{3}\) \(f'(x) = 6x^{5} - 20x^{4} +
4x^{3}\) |
D.  \(f'(x) = 6x^{5} - 20x^{4} -
16x^{3}\) \(f'(x) = 6x^{5} - 20x^{4} -
16x^{3}\) |
Bài 4. Cho hàm số ![]() \(f(x) = \frac{x -
1}{\sqrt{x^{2} + 1}}\). Biết
\(f(x) = \frac{x -
1}{\sqrt{x^{2} + 1}}\). Biết  \(f'(x) = \frac{ax + b}{\left( x^{2} + 1
\right)\sqrt{x^{2} + 1}},\forall x\). Tính giá trị biểu thức
\(f'(x) = \frac{ax + b}{\left( x^{2} + 1
\right)\sqrt{x^{2} + 1}},\forall x\). Tính giá trị biểu thức ![]() \(S = 2a + b\)?
\(S = 2a + b\)?
Bài 5. Cho hàm số ![]() \(y = f(x) = \sqrt{1 -
4x} + \frac{1 - x}{x - 3}\). Tính
\(y = f(x) = \sqrt{1 -
4x} + \frac{1 - x}{x - 3}\). Tính  \(f'(x)\).
\(f'(x)\).
---------------------------------------------------------
Trên đây là hướng dẫn chi tiết cách bấm đạo hàm bằng máy tính cầm tay, đặc biệt với các dòng máy Casio phổ biến như fx-570VN Plus và fx-580VN X. Việc sử dụng thành thạo chức năng tính đạo hàm sẽ giúp bạn tiết kiệm thời gian và tăng độ chính xác khi làm bài kiểm tra hoặc luyện thi. Hãy luyện tập thường xuyên để ghi nhớ thao tác nhanh chóng. Đừng quên chia sẻ bài viết nếu bạn thấy hữu ích và theo dõi thêm nhiều mẹo sử dụng máy tính cầm tay trong môn Toán nhé!


