VnDoc.com

Chuyên đề giới hạn của dãy số

Toán lớp 11

Bài trước

Tải về

Bài sau

Chuyên đề giới hạn của dãy số được VnDoc.com tổng hợp và gửi tới bạn đọc cùng tham khảo nhé.

Chuyên đề giới hạn của dãy số lớp 11

Chi tiết Chuyên đề giới hạn của dãy số lớp 11

CHỦ ĐỀ 1: GIỚI HẠN CỦA DÃY SỐ

Dạng 1: Tìm giới hạn của dãy số

I. Dãy số có giới hạn hữu hạn

1. Định nghĩa:

Ta nói dãy số (u_n) có giới hạn là L hay (u_n) dần tới L khi n dần tới vô cực (n → +oo), nếu lim _{n →+oo} (u_n - L) = 0.

Kí hiệu:

lim_{L→ +oo} (u_n) = L hay u_n → L khi _n→+oo

2. Một số định lý:

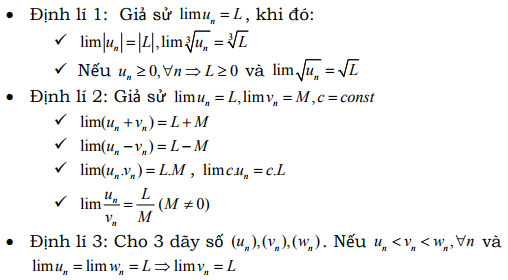
Chi tiết Chuyên đề giới hạn của dãy số lớp 11

Định lí 4: Dãy số tăng và bị chặn trên thì có giới hạn. Dãy số giảm và bị chặn dưới thì có giới hạn.

3. Tổng của cấp số nhân lùi vô hạn

$S = {u_1} + {u_2}q + ... = \frac{{{u_1}}}{{1 - q}};\left( {\left| q \right| < 1} \right)$ $S = u_{1} + u_{2} q + . . . = \frac{u_{1}}{1 - q}; (| q | < 1)$

II. Dãy số có giới hạn vô cực

Dãy số có giới hạn +∞: $\lim {u_n} = + \infty$ $lim u_{n} = + \infty$ ⇔ Mọi số hạng của dãy số đều lớn hơn một số dương tùy ý cho trước kể từ số hạng nào đó trở đi.
Dãy số có giới hạn -∞: $\lim {u_n} = - \infty$ $lim u_{n} = - \infty$ ⇔ Mọi số hạng của dãy số đều nhỏ hơn một số âm tùy ý cho trước kể từ số hạng nào đó trở đi.

Chú ý: $\lim {u_n} = + \infty \to \lim \left( { - {u_n}} \right) = - \infty$ $lim u_{n} = + \infty \to lim (- u_{n}) = - \infty$

Một vài quy tắc tìm giới hạn vô cực

Loại 1: Giới hạn của dãy hữu tỉ

Phương pháp: Xét xem bậc cao nhất của tử và mẫu. Sau đó, chia tử và mẫu cho bậc cao nhất của tử và mẫu. Hoặc cũng có thể đặt nhân tử cao nhất của tử và mẫu để được những giới hạn cơ bản. Tính giới hạn này.

Nhận xét:

Nếu bậc của tử lớn hơn bậc của mẫu thì giới hạn đó bằng +∞ hoặc -∞
Nếu bậc của tử bằng bậc của mẫu thì giới hạn đó bằng hệ số bậc cao nhất của tử trên hệ số bậc cao nhất của mẫu.
Nếu bậc của tử bé hơn bậc của mẫu thì giới hạn đó bằng 0.

Điều này rất cần thiết cho chúng ta giải toán giới hạn dạng hữu tỉ khi giải trắc nghiệm. Bởi vì một giới hạn hữu tỉ khi nhìn vào bài toán có thể biết được kết quả ngay lập tức.

Loại 2: Giới hạn của dãy có căn thức

Phương pháp: Nếu dãy số có chứa căn thức mà không có dạng hữu tỉ để xét bậc, thì ta tiến hạnh nhận thêm lượng liên hợp để tính giới hạn. Nhưng đồng thời các em cũng sử dụng nhận xét ở tính giới hạn hữu tỉ.

Lưu ý:

Biểu thức nhận lượng liên hợp bậc hai: $\left( {A + B} \right)\left( {A - B} \right) = {A^2} - {B^2}$ $(A + B) (A - B) = A^{2} - B^{2}$
Biểu thức nhận lượng liên hợp bậc ba:

$\begin{matrix} \left( {A + B} \right)\left( {{A^2} - AB + {B^2}} \right) = {A^3} + {B^3} \hfill \\ \left( {A - B} \right)\left( {{A^2} + AB + {B^2}} \right) = {A^3} - {B^3} \hfill \\ \end{matrix}$ $\begin{matrix} (A + B) (A^{2} - A B + B^{2}) = A^{3} + B^{3} \\ (A - B) (A^{2} + A B + B^{2}) = A^{3} - B^{3} \end{matrix}$

Sau khi nhận thêm lượng liên hợp thì ta cũng có thể sử dụng nhận xét của giới hạn dãy số hữu tỉ để tính giới hạn nhanh hơn.

Loại 3: Giới hạn của dãy số có chữa lũy thừa - mũ

Phương pháp: Tương tự như dãy số hữu tỉ, ta tiến hành chia tử và mẫu cho mũ với cơ số lớn nhất.

Một số công thức cần lưu ý:

$\frac{{{a^n}}}{{{b^n}}} = {\left( {\frac{a}{b}} \right)^n};{\text{ }}\frac{1}{{{a^n}}} = {a^{ - n}};{\text{ }}\sqrt[n]{a} = {a^{\frac{1}{n}}};{\text{ }}{1^n} = 1$ $\frac{a^{n}}{b^{n}} = {(\frac{a}{b})}^{n}; \frac{1}{a^{n}} = a^{- n}; \sqrt[n]{a} = a^{\frac{1}{n}}; 1^{n} = 1$

Giới hạn của lũy thừa: $\lim {a^n} = 0;\left( {0 < a < 1} \right)$ $lim a^{n} = 0; (0 < a < 1)$ .

Dạng 2. Tính giới hạn bằng chúng minh hoặc theo định nghĩa

Phương pháp 1: Dùng định lí kẹp

Phát biểu: Cho 3 dãy số $\left( {{u_n}} \right);\left( {{v_n}} \right);\left( {{w_n}} \right)$ $(u_{n}); (v_{n}); (w_{n})$ . Nếu ${u_n} < {v_n} < {w_n}$ $u_{n} < v_{n} < w_{n}$ với mọi n và $\lim {u_n} = \lim {w_n} = L \Rightarrow \lim {v_n} = L$ $lim u_{n} = lim w_{n} = L \Rightarrow lim v_{n} = L$

----------------------------------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Chuyên đề giới hạn của dãy số. Hi vọng qua bài viết bạn đọc có thể học tập tốt hơn môn Toán lớp 11. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh cùng tham khảo thêm một số tài liệu học tập các môn tại các mục giải bài tập Toán lớp 11, giải bài tập Toán lớp 10, đề thi học kì 1 lớp 10, Thi thpt Quốc gia môn Toán, mà VnDoc tổng hợp và đăng tải.

Xem thêm các bài Tìm bài trong mục này khác:

Chia sẻ, đánh giá bài viết

8

24.455

Bài trước

Bài sau

Chia sẻ bởi:
Biết Tuốt

Tải về

Chọn file muốn tải về:

Chuyên đề giới hạn của dãy số

450,5 KB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!