Cách bấm máy căn bản cần biết phục vụ kì thi THPT Quốc Gia
Cách bấm máy tính fx 570vn plus Toán 12
Để giúp các bạn học sinh lớp 12 học tập tốt hơn môn Toán, VnDoc xin mời các bạn tham khảo tài liệu Cách bấm máy tính hỗ trợ học sinh làm bài tập trắc nghiệm ôn thi THPT Quốc gia. Tàì liệu được xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12 và ma trận đề thi THPT Quốc gia. Chúc các bạn học tập thật tốt!
- Tìm m để hàm số đồng biến, nghịch biến trên R
- 300 câu hỏi trắc nghiệm môn Toán lớp 12 (Có đáp án)
- Bài tập trắc nghiệm cực trị của hàm số và điểm uốn (Có đáp án)
- Bài tập trắc nghiệm tính đơn điệu của hàm số
- Câu hỏi trắc nghiệm môn Toán lớp 12: Cực trị của hàm s
Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.
1. Bấm các kí tự biến số
- Để gọi một kí tự A, B, C, X, Y, M ta có thể nhấn nút 
kết hợp với các nút có chứa biến số 
2. Công cụ CALC
- Nút 
có tác dụng thay số vào một biểu thức, thử nghiệm của phương trình loại trừ đáp án, …
Ví dụ: Tính giá trị của hàm số 
\(y = \sqrt {2{x^2} + 3x + 1} - x\) tại x = 3
Hướng dẫn
Bước 1: Nhập biểu thức: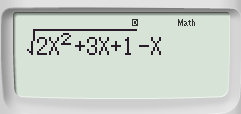 
Bước 2: Bấm CALC, màn hình hiển thị X? ta nhập giá trị 3 rồi nhấn “=” ta thu được kết quả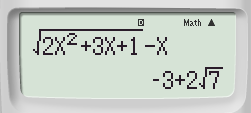 
3. Dò nghiệm của phương trình bằng SOLVE
Để xuất hiện SOLVE ta phải bấm tổ hợp phím SHIFT + CALC
Ví dụ: Tìm nghiệm của phương trình: \(\frac{x}{{12}} - \frac{5}{{16}} = \frac{x}{{40}} - \frac{{19}}{{60}}\)
Hướng dẫn
Bước 1: Nhập phương trình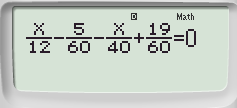 
Bước 2: Nhấn tổ hợp phím SHIFT + CALC: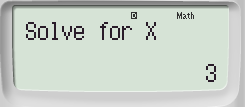 
Bước 3: Nhập một số bất kì thỏa mãn điều kiện xác đinh ví dụ 645555555 
Rồi nhấn “=” ta thu được kết quả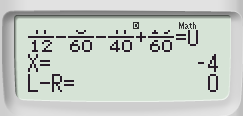 
4. Lập bảng giá trị TABLE
- TABLE là công cụ quan trọng để lập bảng giá trị của hàm số, từ bảng giá trị ta dễ dàng hình dung được hình dạng, xác định được cực trị, giá trị lớn nhất, nhỏ nhất của hàm số.
Ví dụ: Lập bảng giá trị của hàm số \(y = {x^3} - 2x + 1\) trên [1,5]
Hướng dẫn
Bước 1: Chuyển sang công cụ bảng ta nhấn MODE + 7
Bước 2: Nhập hàm số: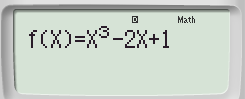 
sau đó bấm “ = “
Bước 3: Máy hiển thị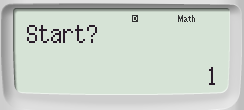 
nhập 1 rồi nhấn “ = “ , máy hiển thị
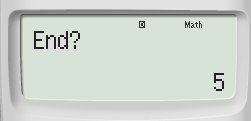nhập 5 rồi nhấn “ = “
Bước 4: Máy hiển thị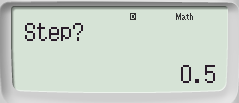 
chọn STEP là 0,5 ta được kết quả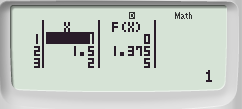 
5. Ứng dụng tính tích phân
Bài toán 1. Ban đầu trong một mẫu nước có khoảng \(600\)con vi khuẩn, trong 1 giờ số lượng này tăng lên với tốc độ \(v(t) =
400e^{1.25t}\). Hỏi sau 3 giờ, 5giờ và 7 giờ số lượng vi khuẩn trong mẫu lần lượt là bao nhiêu?
- \(13886 - 166044 - 2019700\)
- \(17608 - 207805 - 2524875\)
- \(18808 - 210205 - 2528475\)
- \(18702 - 220350 - 2516969\)
Hướng dẫn giải
Cách 1: Đặt \(S(t)\) là số vi khuẩn trong mẫu sau \(t\) giờ
Khi đó ta có: \(S(t) = \int_{}^{}{v(t)dt =
\int_{}^{}{400e^{1.25t}dt = 320e^{1.25t} + C}}\)
Theo đề bài ta có: \(S(0) = 600
\Leftrightarrow 320 + C = 600 \Leftrightarrow C = 280\)
Suy ra: \(S(t) = 320e^{1.25t} +
280\)
Sử dụng Casio fx 580vnx tìm số lượng vi khuẩn sau 3 giờ, 5giờ và 7 giờ
Nhập biểu thức vào máy:
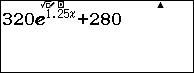
Sử dụng lệnh r lần lượt tại các giá trị \(x
= 3\); \(x = 5\) và \(x = 7\)
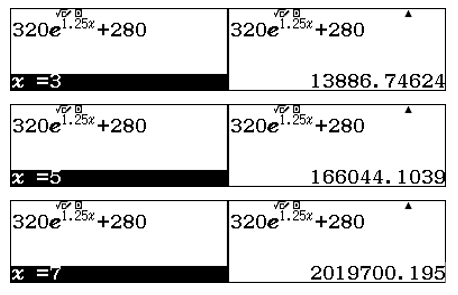
Đáp án A
Cách 2 Đặt \(S(t)\) là số vi khuẩn trong mẫu sau \(t\) giờ
Ta có \(S(t) = S(0) +
\int_{0}^{t}{400e^{1.25x}dx = 600
+}\int_{0}^{t}{400e^{1.25x}dx}\)
Nhập biểu thức vào máy:
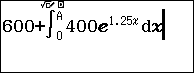
Sử dụng lệnh r lần lượt tại các giá trị \(A
= 3\); \(A = 5\) và \(A = 7\)
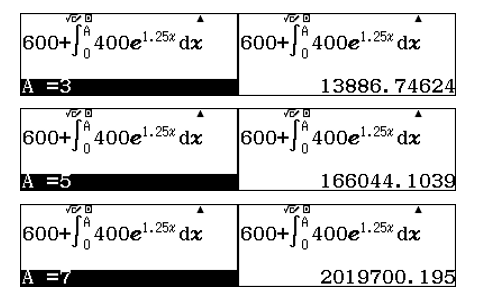
Đáp án A
Bài toán 2. Một công ty dự định đầu tư một khu nhà máy sản xuất. Giả sử sau \(t\) năm, dự án lần 1 có tốc độ phát sinh lợi nhuận là \(P_{1}(t) = 100 +
t^{2}\)trăm đôla/năm, tiếp sau đó dự án lần 2 có tốc độ phát sinh lợi nhuận là \(P_{2}(t) = 150 + 5t\) trăm đôla/năm. Biết rằng sau thời gian \(t\) thì tốc độ lợi nhuận lần 1 gấp 2 lần tốc độ lợi nhuận lần 2. Tính lợi nhuận chênh lệch thực tế cho khoảng thời gian trên
- \(676.66\) trăm đô
- \(755\) trăm đô
- \(750\) trăm đô
- \(666.67\) trăm đô
Hướng dẫn giải
Khoảng thời gian \(t(t > 0)\) để tốc độ lợi nhuận lần 1 gấp 2 lần tốc độ lợi nhuận lần 2 là nghiệm dương của phương trình:
\(P_{1}(t) = 2P_{2}(t) \Leftrightarrow 100
+ t^{2} = 300 + 10t \Leftrightarrow \left\lbrack \begin{matrix}
t = 20 \\
t = - 10 \\
\end{matrix} \right.\)
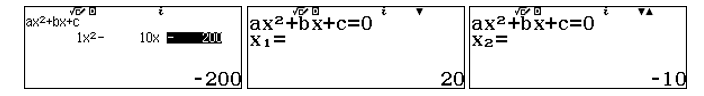
Vậy lợi nhuận chênh lệch thực tế cho khoảng thời gian \(0 \leq t \leq 20\) là
\(\int_{0}^{20}\left\lbrack P_{1}(t) -
P_{2}(t) \right\rbrack dt = \int_{0}^{20}{\left\lbrack \left( 100 +
t^{2} \right) - (150 + 5t) \right\rbrack dt = \int_{0}^{20}{\left( t^{2}
- 5t - 50 \right)dt}}\)
Đáp án D
--------------------------------------------------------------------
Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Cách bấm trắc nghiệm bằng máy tính. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán lớp 12, Thi THPT Quốc gia môn Toán, Thi THPT Quốc gia môn Văn, Thi THPT Quốc gia môn Lịch sử mà VnDoc tổng hợp và đăng tải.
