Cách tìm ma trận nghịch đảo bằng máy tính Casio 580, 570, Matlab, Gauss

Ma trận nghịch đảo là gì? Tính chất của ma trận nghịch đảo và cách tính ma trận nghịch đảo bằng máy tính như thế nào?... Để giúp các bạn giải đáp thắc mắc này, VnDoc gửi tới các bạn tài liệu Cách tính định thức, ma trận nghịch đảo bằng máy tính Casio Fx-570ES để rõ hơn nhé. Sau đây mời các bạn tham khảo chi tiết bài viết dưới đây nhé.

• Tham khảo một số máy tỉnh bỏ túi chất lượng hiện nay
• Hướng dẫn sử dụng và giải toán trên máy tính Casio fx 500MS
• Một số bẫy Casio học sinh dễ mắc và cách khắc phục

I. Ma trận nghịch đảo là gì?

Cho ma trận A vuông cấp n. Ta nói ma trận A là ma trận khả nghịch nếu tồn tại ma trận B sao cho AB = BA = E_n . Khi đó, B gọi là ma trận nghịch đảo của ma trận A, kí hiệu là A^-1.

Như vậy, A.A^-1= A^-1.A= I_n

II. Tính chất của ma trận nghịch đảo

- Điều kiện cần và đủ để ma trận A vuông cấp n khả nghịch là định thức của A là phần tử khả nghịch trong vành V.

- Nếu A là ma trận trên một trường F thì A là khả nghịch khi và chỉ khi định thức của nó khác 0.

- Ma trận đơn vị là ma trận khả nghịch.

- Nếu A, B là các ma trận khả nghịch thì AB khả nghịch và (AB)^-1 = B^-1.A^-1

- Nếu A khả nghịch thì A^T khả nghịch và (A^T)^-1= (A^-1)^T

- Tập hợp các ma trận vuông cấp n trên K khả nghịch, được ký hiệu là GLn(K).

III. Ví dụ về ma trận nghịch đảo

Xét các ma trận vuông thực, cấp 2 sau đây:

Ta có: A.B = B.A = I₂. Do đó: A, B là khả nghịch và A là nghịch đảo của B; B là nghịch đảo của A

Ma trận C không khả nghịch vì với mọi ma trận vuông cấp 2 ta đều có:

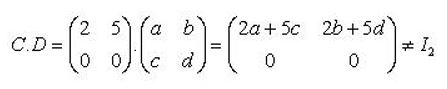
Nhận xét: Ma trận có ít nhất 1 dòng không (hoặc cột không) đều không khả nghịch.

Để tính định thức và tìm ma trận nghịch đảo của ma trận bậc n <= 3×3, ta có thể dùng máy tính bỏ túi Fx – 570ES để tính như sau:

Lưu ý: dấu “–>” chỉ bước tiếp theo phải thực hiện.

IV. Cách tìm ma trận nghịch đảo bằng máy tính 570

1. Cách tìm ma trận nghịch đảo bằng máy tính 580

• Nhấn Mode 6 (Matrix) –> Chọn 1( matA) –> Chọn matrix có số dòng và cột tương ứng cần tính toán. Ví dụ: 1 – ma trận 3 dòng 3 cột.
• Nhập kết quả vào bằng phím =,
• Sau khi nhập xong ma trận A, có thể nhập thêm ma trận B bằng cách: Nhấn Shift 4 (Matrix) –> 1 (Dim) –> 2 (MatB)
• Lập lại tương tự cho MatC.

Ví dụ: Cho ma trận: _{\(A = \left( {\begin{array}{*{20}{c}} 2&1&3\\ { - 3}&1&2\\ 1&2&1 \end{array}} \right)\)}. Hãy nhập dữ liệu ma trận vào máy tính cầm tay.

Hướng dẫn cách bấm máy

Bước 1: Nhấn phím MODE →6( chọn MATRIX)

Bước 2: Nhấn phím 1( chọn ma trận A)

Bước 3: Nhấn phím 1 (chọn dạng ma trận 3 x 3)

Bước 4: Nhập các hạng tử trong ma trận A vào máy tính.

2. Tính định thức

Thao tác như sau để tính định thức cho MatA: Shift 4 (Matrix) –> 7 (Det) –> Shift 4 (Matrix) –> 3 (MatA) –> =

Ví dụ: Tìm định thức của ma trận vuông _{\(A = \left( {\begin{array}{*{20}{c}} 2&1&3\\ { - 3}&1&2\\ 1&2&1 \end{array}} \right)\)}.

Hướng dẫn bấm máy

Bước 1: Nhấn phím MODE →6( chọn MATRIX)

Bước 2: Nhấn phím 1( chọn ma trận A)

Bước 3: Nhấn phím 1 (chọn dạng ma trận 3 x 3). Nhập các hạng tử trong ma trận A vào máy tính. (như ví dụ 1)

Bước 4: Nhấn phím AC→Shift→4→7 (chọn công thức det)

Bước 5: Nhấn phím Shift→4→3 (chọn ma trận A)

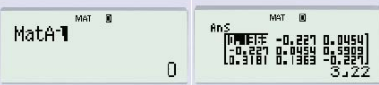
3. Tìm ma trận nghịch đảo

Thao tác như sau để tìm ma trận nghịch đảo của MatA: Shift 4 (Matrix) –> 3 (MatA) –> x^-1 (x^-1: là phím nghịch đảo của máy tính)

Ví dụ: Tìm ma trận nghịch đảo của ma trận _{\(A = \left( {\begin{array}{*{20}{c}} 2&1&3\\ { - 3}&1&2\\ 1&2&1 \end{array}} \right)\)}

Hướng dẫn bấm máy

Bước 1: Nhấn phím MODE →6( chọn MATRIX)

Bước 2: Nhấn phím 1( chọn ma trận A)

Bước 3: Nhấn phím 1 (chọn dạng ma trận 3 x 3). Nhập các hạng tử trong ma trận A vào máy tính. (như ví dụ 1)

Bước 4: Nhấn phím Shift→4→3 (chọn ma trận A)

Bước 5: Nhấn phím x^-1 (tính ma trận nghịch đảo A^-1)

Bước 6: Nhấn phím =

4. Cộng, trừ hai ma trận

Ví dụ: Cho hai ma trận \(A = \left( {\begin{array}{*{20}{c}} 2&1&3\\ { - 3}&1&2\\ 1&2&1 \end{array}} \right),B = \left( {\begin{array}{*{20}{c}} 5&1&2\\ 4&{ - 1}&0\\ 1&1&{ - 3} \end{array}} \right)\). Hãy tính các ma trận A + B; A - 2B

Hướng dẫn bấm máy

Bước 1: Nhấn phím MODE →6( chọn MATRIX)

Bước 2: Nhấn phím 1( chọn ma trận A)

Bước 3: Nhấn phím 1 (chọn dạng ma trận 3 x 3). Nhập các hạng tử trong ma trận A vào máy tính. (như ví dụ 1)

Bước 4: Nhấn phím Shift→4→1→2→∇→2 (nhập ma trận B kích thước 3 x 3)

Bước 5: Nhấn phím Shift→4→3 (chọn ma trận A)

Bước 6: Nhấn phím + hoặc - hoặc x

Bước 7: Nhấn phím Shift→4→4 (chọn ma trận B)

Bước 8: Nhấn phím =

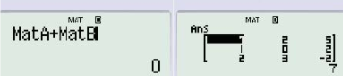
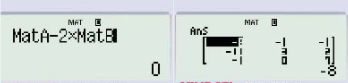
5. Giải phương trình: AX = B

Thao tác theo các bước bên trên để tính: MatA –> x^-1 –> x –> MatB để cho kết quả của X.

Mua máy tính bỏ túi Casio FX-570VN Plus

...................

Trên đây VnDoc đã gửi tới các bạn tài liệu Cách tính định thức, ma trận nghịch đảo bằng máy tính Casio Fx-570ES. Chắc hẳn qua bài viết bạn đọc đã nắm được những ý chính cũng như trau dồi được nội dung kiến thức của bài học rồi đúng không ạ? Bài viết cho chúng ta thấy được cách tính định thức, tính chất của ma trận nghịch đảo, cách bấm ma trận nghịch đảo bằng máu tính Casio... Hy vọng thông qua tài liệu này, các bạn sẽ nắm được thế nào là ma trận nghịch đảo, ví dụ về ma trận nghịch đảo và các bước tính ma trận nghịch đảo bằng máy tính Casio Fx-570ES.

Để tham khảo các tài liệu phục vụ công việc học tập khác, mời các bạn cùng tham khảo vào chuyên mục Học tập trên VnDoc.com nhé.

Để giúp bạn đọc có thể giải đáp được những thắc mắc và trả lời được những câu hỏi khó trong quá trình học tập. VnDoc.com mời bạn đọc cùng đặt câu hỏi tại mục hỏi đáp học tập của VnDoc. Chúng tôi sẽ hỗ trợ trả lời giải đáp thắc mắc của các bạn trong thời gian sớm nhất có thể nhé.