Cách tính khoảng cách giữa hai mặt phẳng
Tính khoảng cách giữa hai mặt phẳng
Trong hình học không gian, việc xác định khoảng cách giữa hai mặt phẳng song song là một kỹ năng quan trọng thường xuất hiện trong các bài kiểm tra, đề thi học kỳ và kỳ thi THPT Quốc gia. Tuy là một chuyên đề nhỏ trong chương trình Toán lớp 12, nhưng nếu nắm chắc cách tính khoảng cách giữa hai mặt phẳng, bạn sẽ dễ dàng giải quyết nhiều dạng bài liên quan đến mặt phẳng, đường thẳng và tọa độ không gian. Bài viết dưới đây sẽ hướng dẫn chi tiết cách xác định khoảng cách 2 mặt phẳng bằng công thức chuẩn, kèm theo ví dụ minh họa cụ thể, giúp bạn tiếp cận kiến thức một cách logic, dễ hiểu và hiệu quả.
A. Cách tính khoảng cách 2 mặt phẳng
1. Khoảng cách giữa hai mặt phẳng song song
Hình vẽ minh họa
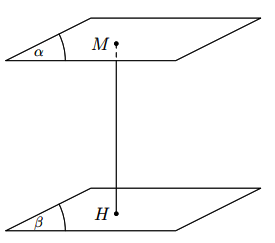
Cho hai mặt phẳng (α) và (β) song song với nhau, khoảng cách từ một điểm bất kì trên mặt phẳng này đến mặt phẳng kia được gọi là khoảng cách giữa hai mặt phẳng (α) và (β).
![]() \(d\left( (\alpha);(\beta) \right) =
d\left( M;(\beta) \right) = d\left( N,(\alpha) \right),M \in (\alpha),N
\in (\beta)\)
\(d\left( (\alpha);(\beta) \right) =
d\left( M;(\beta) \right) = d\left( N,(\alpha) \right),M \in (\alpha),N
\in (\beta)\)
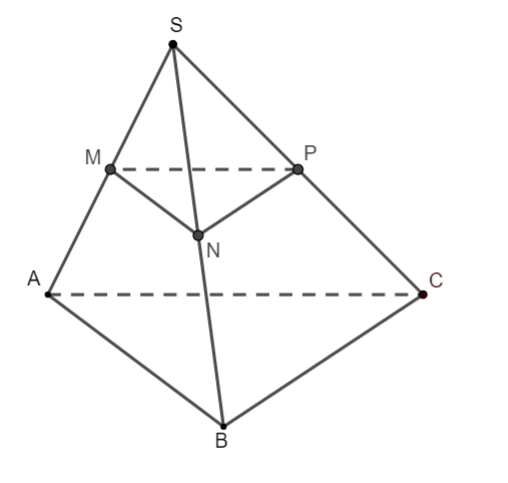
Ví dụ: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng a, mặt bên (SBC) vuông góc với đáy. Gọi M, N, P theo thứ tự là trung điểm AB, SA, AC. Tính khoảng cách giữa hai mặt phẳng (MNP) và (SBC).
Hướng dẫn giải
Hình vẽ minh họa
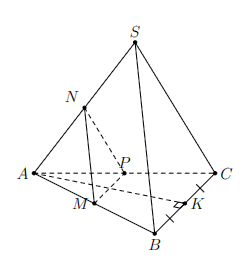
Ta chứng minh được (MNP) // (SBC)
=> d((MNP), (SBC)) = d(P, (SBC))
Giả sử AP ∩ (SBC) = C
=> ![]() \(d\left( P;(SBC) \right) =
\frac{AP}{AC}.d\left( A,(SBC) \right) = \frac{1}{2}d\left( A,(SBC)
\right)\)
\(d\left( P;(SBC) \right) =
\frac{AP}{AC}.d\left( A,(SBC) \right) = \frac{1}{2}d\left( A,(SBC)
\right)\)
Gọi K là trung điểm của BC.
Tam giác ABC đều => AK ⊥ BC
Do (ABC) ⊥ (SBC) theo giao tuyến BC => AK ⊥ (SBC)
=> ![]() \(d\left( A,(SBC) \right) = AK =
\frac{a\sqrt{3}}{2}\)
\(d\left( A,(SBC) \right) = AK =
\frac{a\sqrt{3}}{2}\)
Vậy ![]() \(d\left( (MNP),(SBC) \right) =
\frac{a\sqrt{3}}{4}\)
\(d\left( (MNP),(SBC) \right) =
\frac{a\sqrt{3}}{4}\)
2. Khoảng cách giữa hai đường thẳng chéo nhau
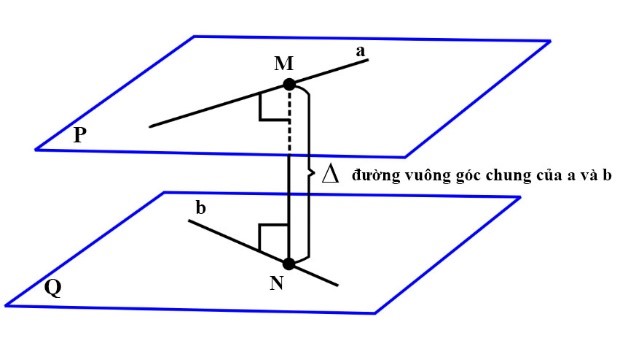
Đường thẳng ∆ cắt hai đường thẳng chéo nhau a, b và vuông góc với cả hai đường thẳng đó được gọi là đường vuông góc chung của a và b.
Nếu đường vuông góc chung ∆ cắt a, b tương ứng tại M, N thì độ dài đoạn thẳng MN được gọi là khoảng cách giữa hai đường thẳng chéo nhau.
Hình vẽ minh họa
Ví dụ: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, ![]() \(SA\bot(ABC)\). Biết rằng SA = AB = BC = a. Tính khoảng cách giữ hai đường thẳng AB và SC?
\(SA\bot(ABC)\). Biết rằng SA = AB = BC = a. Tính khoảng cách giữ hai đường thẳng AB và SC?
Hướng dẫn giải
Hình vẽ minh họa
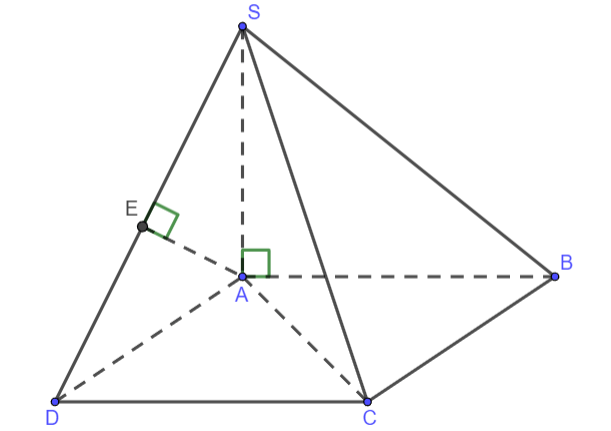
Dựng hình bình hành ABCD vì tam giác ABC vuông cân tại B nên ABCD là hình vuông.
Vì ![]() \(\left\{ \begin{matrix}
CD\bot AD \\
CD\bot SA \\
\end{matrix} \right.\ \Rightarrow CD\bot(SAD)\)
\(\left\{ \begin{matrix}
CD\bot AD \\
CD\bot SA \\
\end{matrix} \right.\ \Rightarrow CD\bot(SAD)\)
Kẻ ![]() \(AE\bot SD\) tại E mà
\(AE\bot SD\) tại E mà ![]() \(AE\bot CD\) nên
\(AE\bot CD\) nên ![]() \(AE\bot(SCD)(*)\)
\(AE\bot(SCD)(*)\)
Vì mặt phẳng (SCD) chứa SC và song song với AB suy ra
![]() \(d(AB;SC) = d\left( AB;(SCD) \right) =
d\left( A;(SCD) \right)(**)\)
\(d(AB;SC) = d\left( AB;(SCD) \right) =
d\left( A;(SCD) \right)(**)\)
Từ (*) và (**) suy ra ![]() \(d(AB;SC) =
AE\)
\(d(AB;SC) =
AE\)
Vì tam giác SAD vuông cân tại A, đường cao AE nên ![]() \(AE = \frac{a\sqrt{2}}{2}\)
\(AE = \frac{a\sqrt{2}}{2}\)
![]() \(\Rightarrow d(AB;SC) =
\frac{a\sqrt{2}}{2}\).
\(\Rightarrow d(AB;SC) =
\frac{a\sqrt{2}}{2}\).
Ví dụ: Cho hình hộp ABCD.A’B’C’D’ có ABCD là hình thoi cạnh a,  \(AA'\bot(ABCD)\);
\(AA'\bot(ABCD)\);  \(AA' = 2a;AC = a\). Tính:
\(AA' = 2a;AC = a\). Tính:
a)  \(d\left( A;(BCC'B')
\right)\).
\(d\left( A;(BCC'B')
\right)\).
b)  \(d\left(
(ABB'A'),(CDD'C') \right)\).
\(d\left(
(ABB'A'),(CDD'C') \right)\).
Hướng dẫn giải
Hình vẽ minh họa
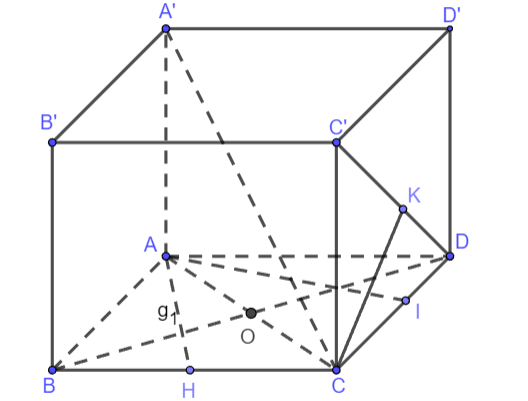
a) Gọi H là hình chiếu của A trên BC
Khi đó  \(AH\bot(BCC'B')\)
\(AH\bot(BCC'B')\)
Vì tam giác ABC đều cạnh bằng a nên ![]() \(AH =
\frac{a\sqrt{3}}{2}\)
\(AH =
\frac{a\sqrt{3}}{2}\)
 \(\Rightarrow d\left( A;(BCC'B')
\right) = \frac{a\sqrt{3}}{2}\)
\(\Rightarrow d\left( A;(BCC'B')
\right) = \frac{a\sqrt{3}}{2}\)
b) Vì ABCD.A’B’C’D’ là hình hộp nên (ABCD)//(CDD’C’)
Gọi I là hình chiếu của A trên CD
Vì tam giác ACD đều cạnh bằng a nên ![]() \(AI =
\frac{a\sqrt{3}}{2}\)
\(AI =
\frac{a\sqrt{3}}{2}\)
 \(\Rightarrow d\left(
(ABB'A'),(CDD'C') \right) =
\frac{a\sqrt{3}}{2}\).
\(\Rightarrow d\left(
(ABB'A'),(CDD'C') \right) =
\frac{a\sqrt{3}}{2}\).
Nhận xét:
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó đến mặt phẳng song song với nó và chứa đường thẳng còn lại.
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song tương ứng chứa hai đường thẳng đó.
II. Bài tập khoảng cách giữa hai mặt phẳng
Câu 1: Chọn mệnh đề sai
Tìm mệnh đề sai trong các mệnh đề sau:
- Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm A bất kì trên a đến (P).
- Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm M bất kì trên mặt phẳng này đến mặt phẳng kia.
- Khoảng cách giữa hai đường thẳng chéo nhau a và b là khoảng cách từ một điểm M thuộc mặt phẳng (P) chứa a và song song với b đến một điểm N bất kì trên b.
- Nếu hai đường thẳng a và b chéo nhau và vuông góc với nhau thì đường vuông góc chung của chúng nằm trong mặt phẳng (P) chứa đường thẳng này và vuông góc với đường thẳng kia.
Câu 2. Cho hình chóp ![]() \(S.ABC\) có
\(S.ABC\) có ![]() \(SA\bot(ABC),SA = h\). Gọi
\(SA\bot(ABC),SA = h\). Gọi ![]() \(M,N,P\) tương ứng là trung điểm của
\(M,N,P\) tương ứng là trung điểm của ![]() \(SA,SB,SC\).
\(SA,SB,SC\).
a) Tính ![]() \(d\left( (MNP),(ABC)
\right)\) và
\(d\left( (MNP),(ABC)
\right)\) và ![]() \(d\left( NP,(ABC)
\right)\).
\(d\left( NP,(ABC)
\right)\).
b) Giả sử tam giác ![]() \(ABC\) vuông tại
\(ABC\) vuông tại ![]() \(B\) và
\(B\) và ![]() \(AB
= a\). Tính
\(AB
= a\). Tính ![]() \(d\left( A,(SBC)
\right)\).
\(d\left( A,(SBC)
\right)\).
Câu 3. Cho hình lập phương  \(ABCD \cdot
A'B'C'D'\) có cạnh
\(ABCD \cdot
A'B'C'D'\) có cạnh ![]() \(a\).
\(a\).
a) Chứng minh rằng hai mặt phẳng  \((D'AC)\) và
\((D'AC)\) và  \((BC'A)\) song song với nhau và
\((BC'A)\) song song với nhau và  \(DB'\) vuông góc với hai mặt phẳng đó.
\(DB'\) vuông góc với hai mặt phẳng đó.
b) Xác định các giao điểm ![]() \(E,F\) của
\(E,F\) của  \(DB'\) với
\(DB'\) với  \((D'AC),(BC'A)\). Tính
\((D'AC),(BC'A)\). Tính  \(d\left( (D'AC),(BC'A)
\right)\).
\(d\left( (D'AC),(BC'A)
\right)\).
Câu 4: Cho lăng trụ đứng ABC.A’B’C’ có AB = AC = BB’ = a, ![]() \(\widehat{BAC} = 120^{0}\). Gọi I là trung điểm của CC’. Tính cosin của góc tạo bởi hai mặt phẳng (ABC) và (AB’I).
\(\widehat{BAC} = 120^{0}\). Gọi I là trung điểm của CC’. Tính cosin của góc tạo bởi hai mặt phẳng (ABC) và (AB’I).
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D với AB = 2a, AD = DC = a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Góc giữa SC và mặt đáy bằng 600. Tính khoảng cách d giữa hai đường thẳng AC và SB?
Câu 6. Cho hình lăng trụ tam giác đều  \(ABC.A'B'C'\) có
\(ABC.A'B'C'\) có  \(AB = a,AA' = 2a\).
\(AB = a,AA' = 2a\).
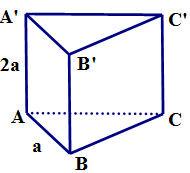
Xét tính đúng sai của các nhận định dưới đây?
a) Khoảng cách giữa hai mặt phẳng ![]() \((ABC)\) và
\((ABC)\) và  \((A'B'C')\) bằng
\((A'B'C')\) bằng ![]() \(2a\).
\(2a\).
b) Khoảng cách giữa đường thẳng  \(B'C'\) và mặt phẳng
\(B'C'\) và mặt phẳng ![]() \((ABC)\) bằng
\((ABC)\) bằng ![]() \(a\).
\(a\).
c) Khoảng cách từ điểṃ ![]() \(A\) đến mặt phẳng
\(A\) đến mặt phẳng  \((BCC'B')\) bằng
\((BCC'B')\) bằng ![]() \(a\).
\(a\).
d) Khoảng cách giữa hai đường thẳng  \(AA'\) và
\(AA'\) và ![]() \(BC\) bằng
\(BC\) bằng ![]() \(a\sqrt{3}\).
\(a\sqrt{3}\).
Câu 7. Cho hình lăng trụ  \(ABC.A'B'C'\) có
\(ABC.A'B'C'\) có  \((A'ABB')\bot(ABC),AA' =
2a,\widehat{A'AB} = 60^{\circ}\). Gọi
\((A'ABB')\bot(ABC),AA' =
2a,\widehat{A'AB} = 60^{\circ}\). Gọi ![]() \(H\) là hình chiếu của
\(H\) là hình chiếu của  \(A'\) trên
\(A'\) trên ![]() \(AB\).
\(AB\).
a) Khoảng cách giữa hai đường thẳng chéo nhau  \(A'C'\) và
\(A'C'\) và ![]() \(AB\) bằng khoảng cách giữa hai mặt phẳng
\(AB\) bằng khoảng cách giữa hai mặt phẳng  \((A'B'C')\) và
\((A'B'C')\) và ![]() \((ABC)\).
\((ABC)\).
b)  \(A'H\) không phải là đoạn vuông góc chung của hai đường thẳng chéo nhau
\(A'H\) không phải là đoạn vuông góc chung của hai đường thẳng chéo nhau  \(A'C'\) 'và
\(A'C'\) 'và ![]() \(AB\).
\(AB\).
c)  \(A'H = a\sqrt{3}\).
\(A'H = a\sqrt{3}\).
d) Khoảng cách giữa hai đường thẳng chéo nhau  \(A'C'\) và
\(A'C'\) và ![]() \(AB\) bằng
\(AB\) bằng ![]() \(a\).
\(a\).
Đáp án bài tập vận dụng
Câu 1.
Mệnh đề sai: “Khoảng cách giữa hai đường thẳng chéo nhau a và b là khoảng cách từ một điểm M thuộc mặt phẳng (P) chứa a và song song với b đến một điểm N bất kì trên b.”
Câu 4.
Hình vẽ minh họa:
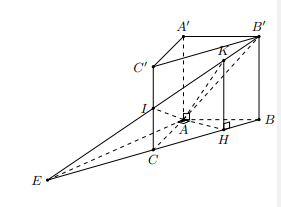
Gọi E là giao điểm của B’I và BC, H thuộc BC sao cho EA ⊥ AH tại A, K ∈ B’I sao cho KH ⊥ CB tại H.
Ta có: KH ⊥ CB => KH // CC’
=> KH ⊥ (ABC) tại H => KH ⊥ EA mà EA ⊥ AH => EA ⊥ (AKH) => EA ⊥ AK
Góc giữa hai mặt phẳng (AIB’) và (ACB) là ![]() \(\widehat{KAH}\)
\(\widehat{KAH}\)
Ta có: BC = 2a.cos 300 = ![]() \(a\sqrt{3}\)
\(a\sqrt{3}\)
Mặt khác AE2 = EC2 + AC2 − 2AC.EC. cos ACE
AE2 = 3a2 + a2 − 2a.![]() \(a\sqrt{3}\).cos 1500= 7a2
\(a\sqrt{3}\).cos 1500= 7a2
=> ![]() \(AE = a\sqrt{7}\)
\(AE = a\sqrt{7}\)
📄 Do dung lượng nội dung lớn, tài liệu chi tiết được cung cấp dưới dạng file tải về.
-------------------------------
Việc nắm vững cách tính khoảng cách giữa hai mặt phẳng song song không chỉ giúp bạn giải nhanh các bài toán trong đề thi mà còn củng cố tư duy không gian và khả năng vận dụng công thức linh hoạt. Qua các ví dụ minh họa trong bài, chắc hẳn bạn đã hiểu rõ hơn về cách áp dụng công thức khoảng cách từ một điểm đến mặt phẳng trong trường hợp đặc biệt khi hai mặt phẳng song song nhau.
Để học tốt chuyên đề khoảng cách 2 mặt phẳng, bạn nên luyện thêm nhiều bài tập thực hành với các dạng toán khác nhau, đồng thời kết hợp kiến thức về vector pháp tuyến, tọa độ điểm và mặt phẳng. Đừng quên lưu lại bài viết này để tham khảo khi cần thiết và theo dõi thêm nhiều nội dung học tập bổ ích khác tại website của chúng tôi – nơi tổng hợp đầy đủ kiến thức Toán học 12 một cách hệ thống, dễ hiểu và chuẩn thi!









