VnDoc.com

Tóm tắt lí thuyết và bài tập Đại số 11 Chương 1

Hàm số lượng giác, Phương trình lượng giác

Tải về

Lớp: Lớp 11

Môn: Toán

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Thư viện Đề thi - Trắc nghiệm - Tài liệu học tập miễn phí

Trang chủ: https://vndoc.com/ | Email hỗ trợ: hotro@vndoc.com | Hotline: 024 2242 6188

Tóm tắt lí thuyết và công thức đại số 11

CHƯƠNG I: HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG

GIÁC KÈM BÀI LUYỆN TẬP

Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

A. TÓM TẮT LÍ THUYẾT VÀ CÔNG THỨC

I. HÀM SỐ LƯỢNG GIÁC

1. Các hàm lượng giác cơ bản

a. Hàm số

sinyx=

• Tập xác định:

D =

• Tập giá trị [-1; 1] hay

1 sinx 1, x−    

b. Hàm số

cosyx=

• Tập xác định:

D =

• Tập giá trị [-1; 1] hay

1 cosx 1, x−    

c. Hàm số

tanyx=

• Tập xác định:

 

\,D k k



=

• Tập giá trị:

d. Hàm số

cotyx=

• Tập xác định:

\,

2

D k k





= + 





• Tập giá trị:

2.Tính tuần hoàn và chu kì

Định nghĩa: Hàm số

( )

y f x=

có tập xác định được gọi là hàm số tuần hoàn, nếu

tồn tại một số

0T 

sao cho với mọi

xD

ta có:

Thư viện Đề thi - Trắc nghiệm - Tài liệu học tập miễn phí

Trang chủ: https://vndoc.com/ | Email hỗ trợ: hotro@vndoc.com | Hotline: 024 2242 6188

•

x T D

−





+



•

( ) ( )

f x T f x+=

Số dương T nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kì của hàm số

tuần hoàn đó. Người ta chứng minh được:

•

sinyx=

tuần hoàn với chu kì

2T



=

•

cosyx=

tuần hoàn với chu kì

2T



=

•

tanyx=

tuần hoàn với chu kì

T



=

•

cotyx=

tuần hoàn với chu kì

T



=

Chú ý:

✓ Hàm số

( )

siny ax b=+

tuần hoàn với chu kì

2

T

a



=

✓ Hàm số

( )

cosy ax b=+

tuần hoàn với chu kì

2

T

a



=

✓ Hàm số

( )

tany ax b=+

tuần hoàn với chu kì

T

a



=

✓ Hàm số

( )

coty ax b=+

tuần hoàn với chu kì

T

a



=

Đặc biệt:

i. Hàm số

( )

sin cos , ,y a mx b nx c m n= + + 

là hàm số tuần hoàn với chu kì

( )

2

,

T

mn



=

với (m,n) là ước chung lớn nhất

ii. Hàm số

( )

tan cot , ,y a mx b nx c m n= + + 

là hàm số tuần hoàn với chu kì

( )

,

T

mn



=

với (m,n) là ước chung lớn nhất

3.Hàm số chẵn lẻ

Hàm số

( )

y f x=

có tập xác định D ta có:

( ) ( )

,,x x D f x f x −  = −



Hàm số được gọi là hàm số chẵn

Hàm số

( )

y f x=

có tập xác định D ta có:

( ) ( )

,,x x D f x f x −  = − −



Hàm số được gọi là hàm số lẻ

Thư viện Đề thi - Trắc nghiệm - Tài liệu học tập miễn phí

Trang chủ: https://vndoc.com/ | Email hỗ trợ: hotro@vndoc.com | Hotline: 024 2242 6188

II. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN

1. Phương trình lượng giác cơ bản

✓

( )

2

sin sin

2

x a k







=+

=  



= − +



✓

( )

2

cos cos

2

x a k





=+

=  



= − +



✓

( )

tan tanx a x a k k



=  = + 

✓

( )

cot cotx a x a k k



=  = + 

2. Phương trình lượng giác cơ bản đặc biệt

✓

( )

sin 0 ,x x k k



=  = 

✓

( )

sin 1 2 ,

2

x x k k



=  = + 

✓

( )

sin 1 2 ,

2

x x k k



= −  = − + 

✓

( )

cos 0 ,

2

x x k k



=  = + 

✓

( )

cos 1 2 ,x x k k



=  = 

✓

( )

cos 1 2 ,x x k k



= −  = + 

•

( )

tan 1 ,

4

x x k k



=  = + 

•

( )

tan 0 ,x x k k



=  = 

•

( )

tan 1 ,

4

x x k k



= −  = − + 

•

( )

cot 1 ,

4

x x k k



= −  = − + 

•

( )

cot 1 ,

4

x x k k



=  = + 

•

( )

cot 0 ,

2

x x k k



=  = + 

3. Bảng giá trị cung và góc lượng giác đặc biệt

Chú ý:

0

180 1



→

III. CÁC PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH LƯỢNG GIÁC

Dạng 1: Phương trình bậc nhất đối với hàm số lượng giác

sin 0a x b+=

,

cos 0a x b+=

,

tan 0a x b+=

,

cot 0a x b+=

( )

, , 0a b a

Công thức Toán 11: Hàm số lượng giác, Phương trình lượng giác

I. HÀM SỐ LƯỢNG GIÁC
II. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
III. CÁC PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH LƯỢNG GIÁC
B. BÀI TẬP TRẮC NGHIỆM

VnDoc.com xin giới thiệu tới bạn đọc tài liệu: Tóm tắt lí thuyết và bài tập Đại số 11 Chương 1. Bao gồm toàn bộ kiến thức trọng tâm Chương 1 Đại số lớp 11 kết hợp bài tập trắc nghiệm có đáp án. Tài liệu được VnDoc biên soạn và đăng tải, hi vọng sẽ giúp các bạn tổng hợp kiến thức cơ bản Đại số 11 và ôn tập kiến thức môn Toán 11 về Hàm số lượng giác và Phương trình lượng giác hiệu quả, sẵn sàng cho những kì thi sắp tới. Mời các bạn tham khảo và tải về miễn phí tại đây!

I. HÀM SỐ LƯỢNG GIÁC

1. Các hàm lượng giác cơ bản

a. Hàm số $y = \sin x$

b. Hàm số $y = \cos x$

c. Hàm số $y = \tan x$

d. Hàm số $y = \cot x$

2. Tính tuần hoàn và chu kì

Định nghĩa: Hàm số $y = f(x)$ có tập xác định được gọi là hàm số tuần hoàn, nếu tồn tại một số $T \neq 0$ sao cho với mọi $x \in D$ ta có:

$\left\{ \begin{matrix} x - T \in D \\ x + T \in D \\ \end{matrix} \right.$
$f(x + T) = f(x)$

3. Hàm số chẵn lẻ

Hàm số $y = f(x)$ có tập xác định D ta có: $\forall x, - x \in D,f(x) = f( - x)$

$\Rightarrow$ Hàm số được gọi là hàm số chẵn

Hàm số $y = f(x)$ có tập xác định D ta có: $\forall x, - x \in D,f(x) = - f( - x)$

$\Rightarrow$ Hàm số được gọi là hàm số lẻ

II. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN

1. Phương trình lượng giác cơ bản

$\sin x = \sin a \Leftrightarrow \left\lbrack \begin{matrix} x = a + k2\pi \\ x = \pi - a + k2\pi \\ \end{matrix} \right.\ \left( k\mathbb{\in Z} \right)$
$\cos x = \cos a \Leftrightarrow \left\lbrack \begin{matrix} x = a + k2\pi \\ x = - a + k2\pi \\ \end{matrix} \right.\ \left( k\mathbb{\in Z} \right)$
$\tan x = \tan a \Leftrightarrow x = a + k\pi\left( k\mathbb{\in Z} \right)$
$\cot x = \cot a \Leftrightarrow x = a + k\pi\left( k\mathbb{\in Z} \right)$

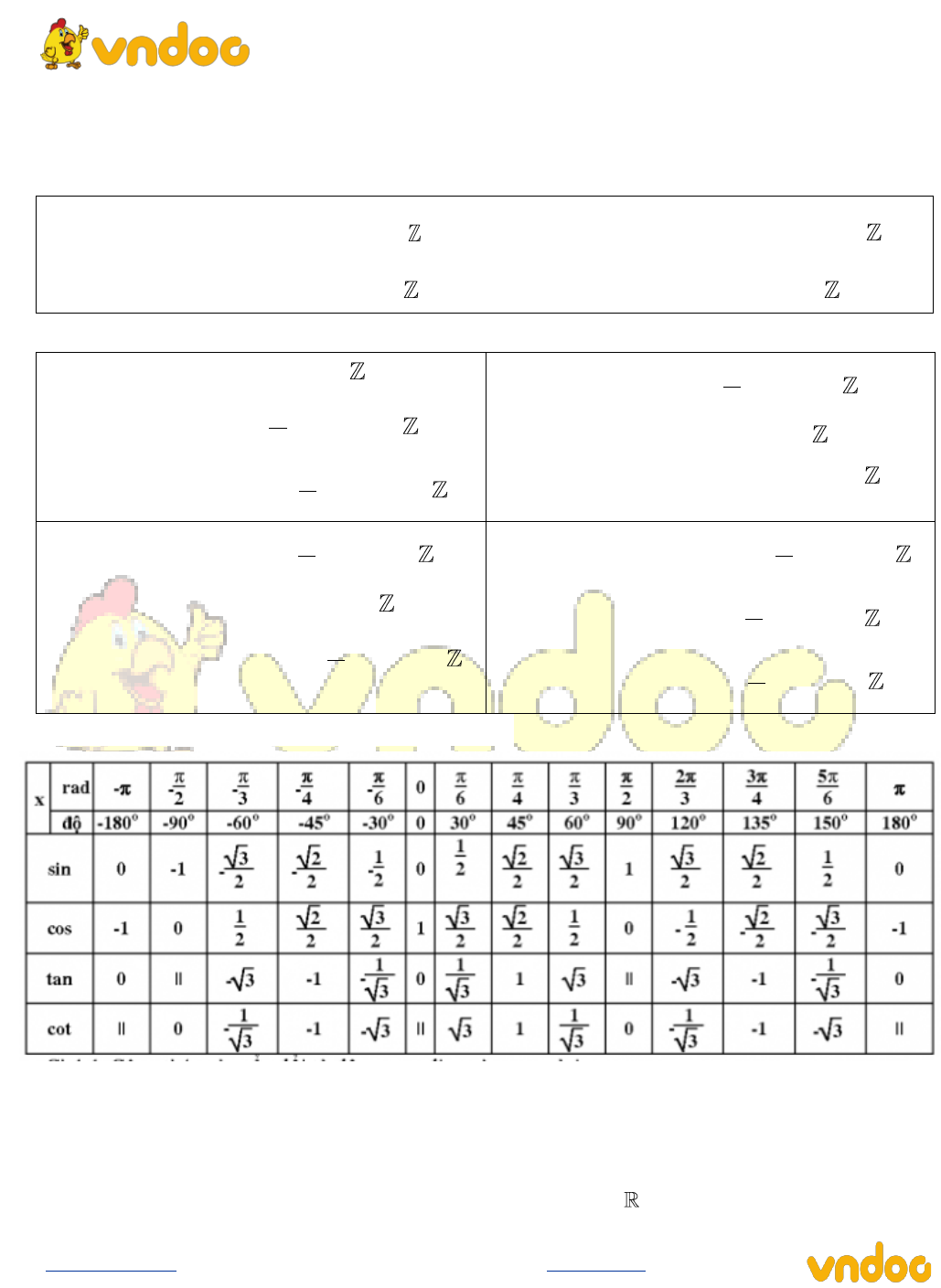
2. Phương trình lượng giác cơ bản đặc biệt

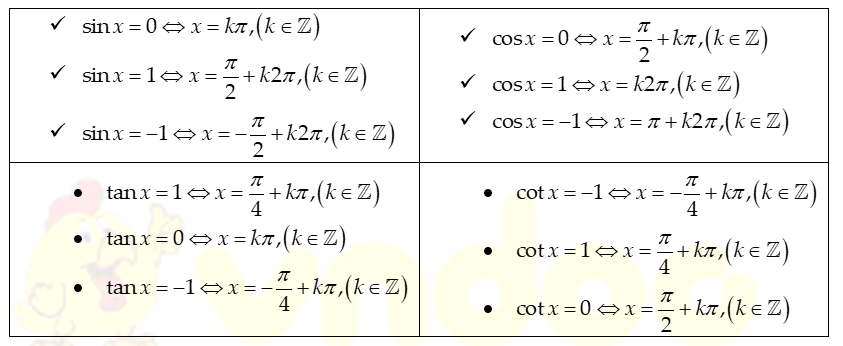
3. Bảng giá trị cung và góc lượng giác đặc biệt

III. CÁC PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH LƯỢNG GIÁC

Dạng 1: Phương trình bậc nhất đối với hàm số lượng giác

$a\sin x + b = 0$ , $a\cos x + b = 0$ , $a\tan x + b = 0$ , $a\cot x + b = 0\left( a,b\mathbb{\in R},a \neq 0 \right)$

Phương pháp: Đưa về dạng phương trình cơ bản như: $\sin x = \frac{- b}{a}$ , $\cos x = \frac{- b}{a}$

Dạng 2: Phương trình bậc hai đối với hàm số lượng giác

Phương pháp: Đặt ẩn đưa về dạng phương trình bậc hai với t

Dạng 3: Phương trình bậc nhất đối với sinx, cosx

Phương trình có dạng: $a\sin x + b\cos x = c,(a \neq 0,b \neq 0)$

Phương pháp: Chia cả 2 vế cho $\sqrt{a^{2} + b^{2}}$ ta được:

$\frac{a}{\sqrt{a^{2} + b^{2}}}\sin x + \frac{b}{\sqrt{a^{2} + b^{2}}}\cos x = \frac{c}{\sqrt{a^{2} + b^{2}}}$

Nếu $\left| \frac{b}{\sqrt{a^{2} + b^{2}}} \right| > 1$ thì phương trình vô nghiệm

Nếu $\left| \frac{b}{\sqrt{a^{2} + b^{2}}} \right| \leq 1$ thì đặt $\cos\beta = \frac{a}{\sqrt{a^{2} + b^{2}}}$ , $\sin\beta = \frac{b}{\sqrt{a^{2} + b^{2}}}$

Đưa phương trình về dạng: $\sin(x + \beta) = \frac{c}{\sqrt{a^{2} + b^{2}}}$

Chú ý: Phương trình $a\sin x + b\cos x = c,(a \neq 0,b \neq 0)$ có nghiệm khi $c^{2} \leq a^{2} + b^{2}$

Dạng 4: Phương trình thuần nhất đối với sinx và cosx

Dạng phương trình: $asin^{2}x + b\sin x\cos x + ccos^{2}x = d$

Phương pháp:

- Nếu cosx = 0. Thế vào phương trình thử nghiệm.

- Nếu $\cos x \neq 0$ . Chia cả 2 vế của phương trình cho $cos^{2}x$ rồi tiến hành giải phương trình bậc hai đối với tanx: $(a - d)tan^{2}x + b\tan x + c - d = 0$ .

B. BÀI TẬP TRẮC NGHIỆM

Câu 1: Tìm tập giá trị của hàm số sau: $y= \sqrt{2 - \sin2x}$ ?

A. $\lbrack 1,2\rbrack$

B. $\left\lbrack 1,\sqrt{3} \right\rbrack$

C. $\left( 1,\sqrt{3} \right)$

D. $(1,2)$

Câu 2: Tập điều kiện của hàm số $y =\frac{1}{\sin x} + \frac{2}{\cos2x}$ ?

A. $\left\{ \begin{matrix}x \neq k\pi \\x \neq \dfrac{\pi}{2} + k\pi\end{matrix} \right.$	B. $\left\{ \begin{matrix}x \neq k2\pi \\x \neq \dfrac{\pi}{2} + k2\pi\end{matrix} \right.$
C. $\left\{ \begin{matrix}x \neq \dfrac{k\pi}{2} \\x \neq \dfrac{\pi}{4} + \dfrac{k\pi}{2}\end{matrix} \right.$	D. $\left\{ \begin{matrix}x \neq k\pi \\x \neq \dfrac{\pi}{4} + \dfrac{k\pi}{2}\end{matrix} \right.$

Câu 3: Tập điều kiện của hàm số: $y = \frac{1}{(x - 1)\left( \sin x + 1 \right)}$ ?

A. $x \neq 1,x \neq \frac{\pi}{2} + k\pi$	B. $x \neq 1,x \neq \frac{\pi}{2} + k2\pi$
C. $x \neq 1,x \neq \frac{- \pi}{2} + k\pi$	D. $x = 1,x \neq \frac{\pi}{2} + k\pi$

Câu 4: Tìm điều kiện xác định của hàm số: $y = \frac{\cos^{2}x + \sin3x}{\sin x}$ ?

A. $x \neq k\pi$	B. $x \neq k2\pi$
C. $x \neq \frac{\pi}{2} + k\pi$	D. $x \neq \frac{\pi}{2} + k2\pi$

Câu 5: Hàm số $y = \tan x$ xác định khi nào?

A. $x \neq \frac{\pi}{2} + k2\pi$	B. $x \neq \frac{\pi}{2} + k\pi$
C. $x \neq k2\pi$	D. $x \neq k\pi$

Câu 6: Tập giá trị của hàm số $y =\sqrt{\frac{\sin2x}{2}}$ .

A. $x\mathbb{\in R}$	B. $\lbrack 0,1\rbrack$
C. $\left\lbrack 0,\frac{1}{\sqrt{2}} \right\rbrack$	D. $\left\lbrack - \frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}} \right\rbrack$

Câu 7: Điều kiện xác định của hàm số: $y =\frac{5\sin x}{\sin x - 1}$ là:

A. $x \neq \frac{- \pi}{2} + k2\pi$	B. $x \neq \frac{\pi}{2} + k2\pi$
C. $x \neq k2\pi$	D. $x \neq k\pi$

Câu 8: Tập xác định của hàm số $y =\frac{2020}{\cos^{3}x}$ .

A. $x\mathbb{\in R}\backslash\left\{ k2\pi \right\}$	B. $x\mathbb{\in R}\backslash\left\{ k\pi \right\}$
C. $x\mathbb{\in R}\backslash\left\{ \frac{- \pi}{2} + k2\pi \right\}$	D. $x\mathbb{\in R}\backslash\left\{ \frac{\pi}{2} + k2\pi \right\}$

Câu 9: Điều kiện xác định của hàm số: $y = \frac{2sinx}{1 - cos^{2}x}$ :

A. $x \neq k\pi$	B. $x \neq k2\pi$
C. $x \neq \frac{- \pi}{2} + k2\pi$	D. $x \neq \frac{\pi}{2} + k2\pi$

Câu 10: Tập giá trị của hàm số: $y =\sqrt{4 - 2\sin x}$ :

A. $\left( \sqrt{2},6 \right)$	B. $\left\lbrack \sqrt{2},6 \right\rbrack$
C. $(2,6)$	D. $\lbrack 2,6\rbrack$

Câu 11: Tìm tập xác định của hàm số: $y =\cot x - \sin3x$ :

A. $x\mathbb{\in R}$	B. $x\mathbb{\in R}\backslash\left\{ k\pi \right\}$
C. $x\mathbb{\in R}\backslash\left\{ \frac{\pi}{2} + k\pi \right\}$	D. $x\mathbb{\in R}\backslash\left\{ \frac{\pi}{2} + k2\pi \right\}$ .

Câu 12: Hàm số $y = \frac{2\cos^{2}2x -x}{x.\cos x}$ xác định khi:

A. $x \neq 0,x \neq \frac{\pi}{2}$	B. $x \neq k\pi$
C. $x \neq 0,x \neq \frac{\pi}{2} + k\pi$	D. $x \neq k2\pi$

Câu 13: Hàm số nào sau đây là hàm số chẵn?

A. $y = x\cos x$	B. $y = \cos x.\tan2x$
C. $y = \sin3x$	D. $y = \frac{\tan x}{\sin x}$

Câu 14: Tính chất của hàm số $y = \frac{1 - \sin x}{1 + \sin x}$ là:

A. Hàm số lẻ	B. Hàm số chẵn
C. Hàm số không chẵn, không lẻ	D. Hàm hằng

Câu 15: Hàm số $y = 2\cos^{2}x - 1$ có chu kì cơ sở là

A. $T = 2\pi$	B. $T = \frac{\pi}{2}$
C. $T = \frac{\pi}{3}$	D. $T = \pi$

Câu 16: Hàm số nào sau đây là hàm số chẵn?

A. $y = \sin x$	B. $y = - \sin x$
C. $y = - 2\cos x$	D. $y = \sin x - \cos x$

Câu 17: Trong các khẳng định sau, khẳng định nào đúng?

A. Hàm số $y = \sin x,y = \cos x$ có chu kì $T = \pi$

B. Hàm số $y = \sin(2x + 1)$ có chu kì $T = 2\pi$

C. Hàm số $y = \tan\left( \frac{3}{2} - 4x \right)$ có chu kì $T = \frac{\pi}{4}$

D. Hàm số $y = sin2x$ có chu kì $T = 2\pi$

Câu 18: Hàm số nào sau đây là hàm số lẻ:

A. $y = - 2\cos x$	B. $y = 3\cos x$
C. $y = \sin^{2}2x$	D. $y = 3\sin x$

Câu 19: Tìm m để hàm số sau là hàm số chẵn?

A. $m = 0$	B. $m < 1$
C. $m > 0$	D. $m = 1$

Câu 20: Xét tính chẵn lẻ của hàm số $y =\tan x + 2\sin x$ ?

A. Là hàm số lẻ	B. Là hàm số chẵn
C. Là hàm không chẵn	D. Là hàm không lẻ

------------------------------------------------------------

Trên đây VnDoc đã chia sẻ đến các bạn học sinh Tóm tắt lí thuyết và bài tập Đại số 11 Chương 1. Chắc hẳn qua bài viết bạn đọc đã nắm được những ý chính cũng như trau dồi được nội dung kiến thức của đề thi rồi đúng không ạ? Bài viết nhằm cung cấp cơ sở kiến thức ôn tập cho các bạn học sinh, giúp các bạn chuẩn bị thật tốt cho các kì thi sắp tới. Hi vọng qua bài viết này bạn đọc có thêm tài liệu để học tập tốt hơn môn Toán lớp 11 nhé. Mời các bạn cùng tham khảo thêm tài liệu học tập các môn Ngữ văn lớp 11, Tiếng Anh lớp 11... Chúc các bạn ôn tập thật tốt!

Để giúp bạn đọc có thể giải đáp được những thắc mắc và trả lời được những câu hỏi khó trong quá trình học tập. VnDoc.com mời bạn đọc cùng đặt câu hỏi tại mục hỏi đáp học tập của VnDoc nhé/

Ngoài ra, VnDoc mời bạn đọc tham khảo thêm một số tài liệu liên quan:

Tải về

Chọn file muốn tải về: