Tóm tắt toàn bộ lý thuyết và công thức Đại số 11


Hệ thống lý thuyết và công thức Đại số 11
Chào mừng các bạn đến với bài viết Tóm tắt toàn bộ lý thuyết và công thức Đại số 11. Đây là bài viết tổng hợp tất cả các lý thuyết và công thức quan trọng trong môn Đại số lớp 11, giúp các bạn học sinh dễ dàng nắm bắt và ôn luyện hiệu quả. Bài viết không chỉ cung cấp hệ thống lý thuyết chi tiết mà còn cung cấp các công thức quan trọng để giải quyết các bài toán Đại số nhanh chóng và chính xác. Hãy cùng theo dõi để trang bị cho mình những kiến thức cơ bản và nâng cao trong Đại số 11!
Nội dung tài liệu bao gồm kiến thức:
CHƯƠNG I: HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
1. Hàm số lượng giác
- Các hàm lượng giác cơ bản
- Tính tuần hoàn và chu kì của hàm số lượng giác
- Hàm số chẵn lẻ
2.Phương trình lượng giác cơ bản
- Phương trình lượng giác cơ bản
- Phương trình lượng giác cơ bản đặc biệt
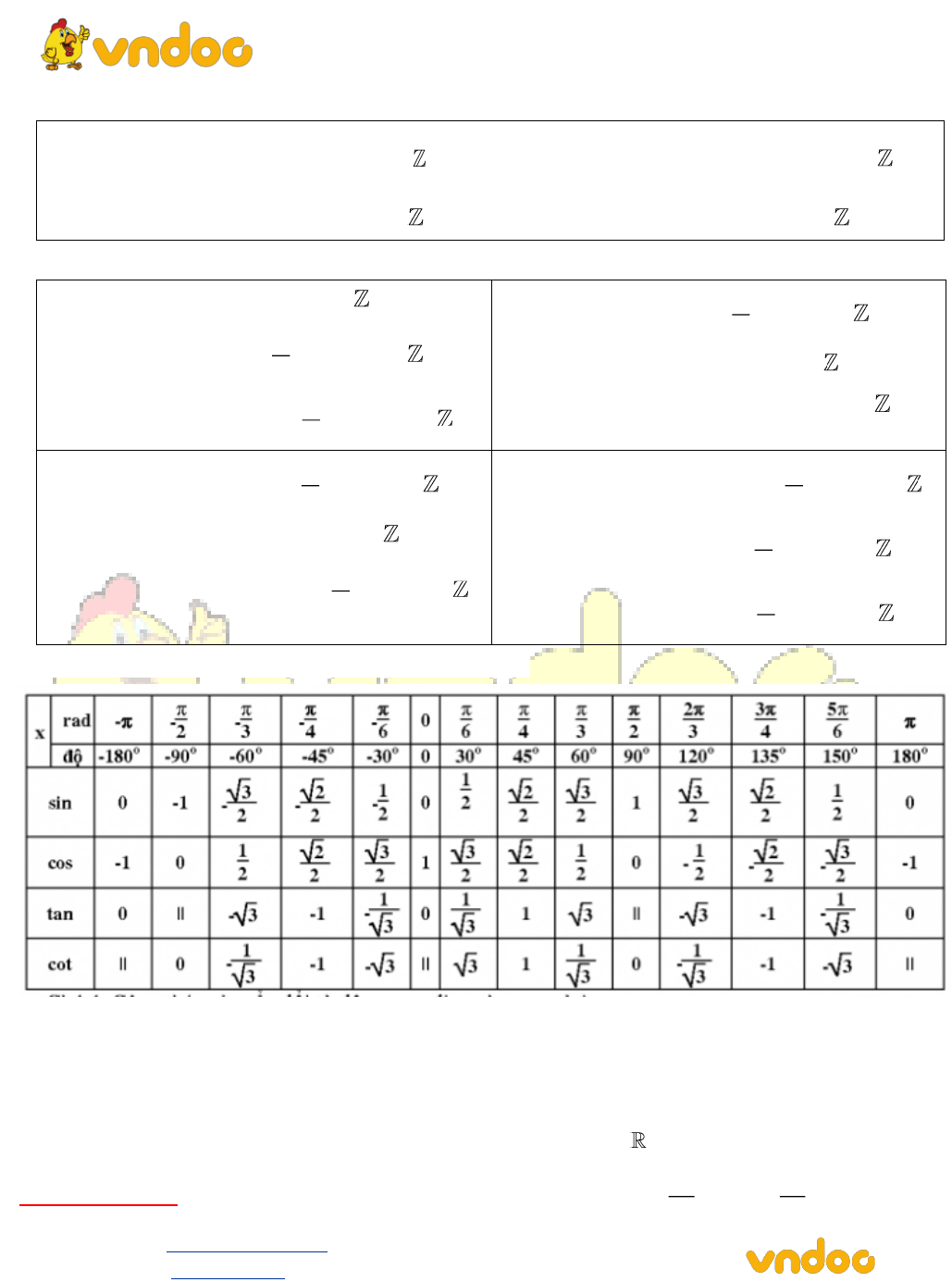
- Bảng giá trị cung và góc lượng giác đặc biệt
- Các phương pháp giải phương trình lượng giác
- Dạng 1: Phương trình bậc nhất đối với hàm số lượng giác
- Dạng 2: Phương trình bậc hai đối với hàm số lượng giác
- Dạng 3: Phương trình bậc nhất đối với sinx, cosx
- Dạng 4: Phương trình thuần nhất đối với sinx và cosx
CHƯƠNG II: TỔ HỢP – XÁC SUẤT
1. Quy tắc đếm
- Quy tắc cộng
- Phương pháp đếm bài toán tổ hợp theo quy tắc cộng
- Quy tắc nhân
- Phương pháp đếm bài toán tổ hợp theo quy tắc nhân
- Các dạng bài toán đếm thường gặp
2. Hoán vì, chỉnh hợp, tổ hợp
3. Xác suất của biến cố
- Định nghĩa xác suất cổ điển
- Định nghĩa thống kê của xác suất
- Phương pháp xác định không gian mẫu và biến cố
4. Nhị thức Newton
CHƯƠNG III. DÃY SỐ - CẤP SỐ CỘNG – CẤP SỐ NHÂN
1. Dãy số
- Cách xác định dãy số
- Dãy số tăng, dãy số giảm
- Dãy số bị chặn
2. Cấp số cộng
- Số hạng tổng quát
- Tính chất
- Tổng của một cấp số cộng
3. Cấp số nhân
- Số hạng tổng quát
- Tính chất
- Tổng của một cấp số nhân
3. Cấp số nhân
CHƯƠNG IV: GIỚI HẠN
1. Hàm số liên tục
2. Giới hạn của hàm số
- Các giới hạn đặc biệt
- Quy tắc giới hạn hữu hạn
- Quy tắc giới hạn vô cực
3. Giới hạn của dãy số
- Các giới hạn đặc biệt
Quy tắc giới hạn hữu hạn
Quy tắc giới hạn vô cực
CHƯƠNG V: ĐẠO HÀM
1. Định nghĩa và ý nghĩa của đạo hàm
2. Quy tắc tính đạo hàm
3. Đạo hàm cấp cao
CHƯƠNG VI: CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CỦA MẪU SỐ LIỆU GHÉP NHÓM
1. Số trung bình của mẫu số liệu ghép nhóm
2. Trung vị của mẫu số liệu ghép nhóm
3. Tứ phân vị của mẫu số liệu ghép nhóm
4. Mốt của mẫu số liệu ghép nhóm
-----------------------------------------------------------
Hy vọng rằng bài viết "Tóm tắt toàn bộ lý thuyết và công thức Đại số 11" đã giúp bạn hệ thống lại các kiến thức quan trọng trong môn Đại số lớp 11. Việc nắm vững lý thuyết và công thức sẽ là nền tảng vững chắc để bạn giải quyết các bài tập và đạt kết quả cao trong kỳ thi. Hãy luôn ôn tập và áp dụng các công thức vào các bài toán thực tế để cải thiện khả năng giải quyết vấn đề. Chúc bạn học tốt và đạt thành tích xuất sắc!



