Cách tính góc nhị diện
Cách Tính Góc Nhị Diện Giữa Hai Mặt Phẳng Trong Hình Học Không Gian
Cách tính góc nhị diện là một trong những vấn đề quan trọng và thú vị trong hình học không gian. Việc xác định góc giữa hai mặt phẳng trong không gian 3D không chỉ giúp bạn giải quyết các bài toán hình học mà còn có ứng dụng rộng rãi trong các lĩnh vực như kỹ thuật, vật lý, cơ học, và thiết kế kiến trúc. Tuy nhiên, nhiều bạn học sinh, sinh viên và những người mới bắt đầu học môn hình học không gian thường gặp khó khăn trong việc tính toán chính xác góc nhị diện.
Trong bài viết này, chúng tôi sẽ hướng dẫn bạn cách tính góc nhị diện một cách nhanh chóng và chính xác, đồng thời cung cấp những phương pháp và công thức hữu ích giúp bạn dễ dàng áp dụng vào thực tế. Bất kể bạn là người mới học hay đang tìm kiếm cách tối ưu hóa quá trình giải bài toán, bài viết này sẽ giúp bạn hiểu rõ và làm chủ được phương pháp tính góc nhị diện.
1. Góc nhị diện là gì?
Góc nhị diện là hình gồm hai nửa mặt phẳng có chung bờ.
Minh họa
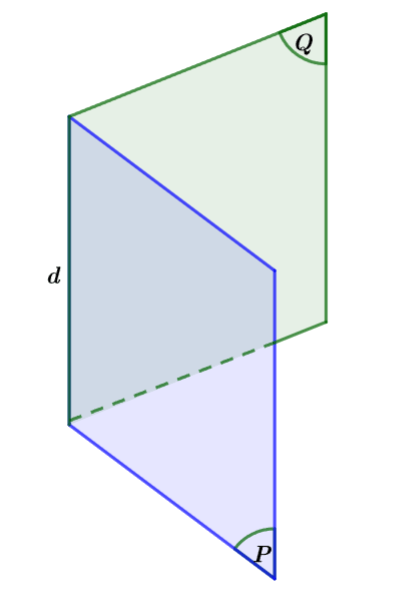
- Đường thẳng
 \(d\) được gọi là cạnh của góc nhị diện, mỗi nửa mặt phẳng
\(d\) được gọi là cạnh của góc nhị diện, mỗi nửa mặt phẳng  \((P)\) và
\((P)\) và  \((Q)\)gọi là một mặt của góc nhị diện.
\((Q)\)gọi là một mặt của góc nhị diện. - Kí hiệu là
 \(\lbrack P,d,Q\rbrack\).
\(\lbrack P,d,Q\rbrack\).
Chú ý: Góc nhị diện còn được kí hiệu là ![]() \(\lbrack A,d,B\rbrack\) với
\(\lbrack A,d,B\rbrack\) với ![]() \(A,B\) lần lượt là các điểm thuộc các nửa mặt phẳng
\(A,B\) lần lượt là các điểm thuộc các nửa mặt phẳng ![]() \((P)\) và
\((P)\) và ![]() \((Q)\).
\((Q)\).
2. Số đo của góc nhị diện
- Số đo của góc phẳng nhị diện
 \(xOy\) không phụ thuộc vào vị trí của điểm
\(xOy\) không phụ thuộc vào vị trí của điểm  \(O\) trên cạnh nhị diện và được gọi là đó của góc nhị diện đã cho.
\(O\) trên cạnh nhị diện và được gọi là đó của góc nhị diện đã cho. - Số đo của góc nhị diện từ
 \(0^{0}\) đến
\(0^{0}\) đến  \(180^{0}\).
\(180^{0}\).
Minh họa
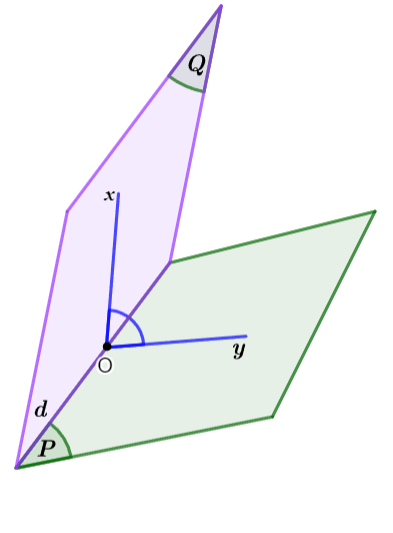
Trong không gian, cho góc nhị diện:
- Một góc có đỉnh thuộc cạnh của góc nhị diện, hai cạnh của góc đó lần lượt thuốc hai mặt phẳng vuông góc với cạnh của góc nhị diện, được gọi là góc phẳng nhị diện của góc nhị diện đã cho.
- Số đo của một góc phẳng nhị diện được gọi là số đo của góc nhị diện đó.
- Nếu số đo góc phẳng nhị diện bằng
 \(90^{0}\) thì góc nhị diện đó gọi là góc nhị diện vuông.
\(90^{0}\) thì góc nhị diện đó gọi là góc nhị diện vuông.
Chú ý:
- Hai mặt phẳng cắt nhau theo giao tuyến d tạo thành bốn góc nhị diện.
- Mỗi đường thẳng d trong một mặt phẳng chia mặt phẳng thành hai phần, mỗi phần cùng với d là một nửa mặt phẳng bờ d.
3. Góc phẳng nhị diện
Góc phẳng nhị diện của góc nhị diện là góc có đỉnh nằm trên cạnh của nhị diện có hai cạnh lần lượt nằm trên hai mặt của nhị diện và vuông góc với cạnh của nhị diện.
Chú ý:
a) Đối với một góc nhị diện, các góc phẳng nhị diện đều bằng nhau.
b) Nếu mặt phẳng (R) vuông góc với cạnh d của góc nhị diện và cắt hai mặt (P) và (Q) của góc nhị diện theo hai nửa đường thẳng Ou và Ov thì uOv là góc phẳng nhị diện của góc nhị diện tạo bởi (P) và (Q).
c) Góc nhị diện có góc phẳng nhị diện là góc vuông được gọi là góc nhị diện vuông.
d) Số đo góc phẳng nhị diện được gọi là số đo góc nhị diện.
e) Số đo góc nhị diện nhận giá trị từ 00 đến 1800.
4. Bài tập minh họa tính góc nhị diện
Ví dụ 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, biết (SAB) ⊥ (ABCD), (SAD) ⊥ (ABCD) và SA= a. Tính côsin của số đo góc nhị diện [S; BD; C] và góc nhị diện [B; SC; D].
Hướng dẫn giải
Hình vẽ minh họa
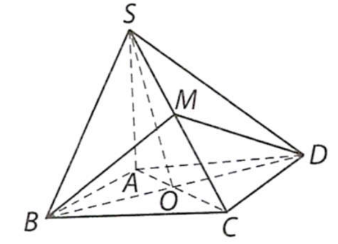
Ta có:
SO ⊥BD; CO⊥ BD nên góc nhị diện [S; BD; C] bằng góc SOC.
Vì tam giác SAO vuông tại A nên ![]() \(SO =
\sqrt{SA^{2} + AO^{2}} = \frac{a\sqrt{6}}{2}\) và
\(SO =
\sqrt{SA^{2} + AO^{2}} = \frac{a\sqrt{6}}{2}\) và ![]() \(\cos\widehat{SOC} = - \cos\widehat{SOA} = -
\frac{OA}{SO} = \frac{- \sqrt{3}}{3}\)
\(\cos\widehat{SOC} = - \cos\widehat{SOA} = -
\frac{OA}{SO} = \frac{- \sqrt{3}}{3}\)
Kẻ BM⊥ SC tại M thì DM ⊥ SC nên [B; SC; D] là góc BMD.
Ta có BC⊥(SAB) nên tam giác SBC vuông tại B, tính được:
 \(\left\{ \begin{matrix}
SB = a\sqrt{2};SC = a\sqrt{3} \\
DM = BM = \dfrac{SB.BC}{SC} = \dfrac{a\sqrt{6}}{3} \\
\end{matrix} \right.\)
\(\left\{ \begin{matrix}
SB = a\sqrt{2};SC = a\sqrt{3} \\
DM = BM = \dfrac{SB.BC}{SC} = \dfrac{a\sqrt{6}}{3} \\
\end{matrix} \right.\)
Áp dụng định lí côsin trong tam giác BDM, ta có:
![]() \(\cos\widehat{BMD} = \frac{BM^{2} +
DM^{2} - BD^{2}}{2BM.DM} = - \frac{3}{4}\)
\(\cos\widehat{BMD} = \frac{BM^{2} +
DM^{2} - BD^{2}}{2BM.DM} = - \frac{3}{4}\)
Ví dụ 2. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy và ![]() \(SA = \frac{a\sqrt{2}}{2}\). Tính số đo góc nhị diện
\(SA = \frac{a\sqrt{2}}{2}\). Tính số đo góc nhị diện ![]() \(\lbrack S,BD,C\rbrack\).
\(\lbrack S,BD,C\rbrack\).
Hướng dẫn giải
Hình vẽ minh họa
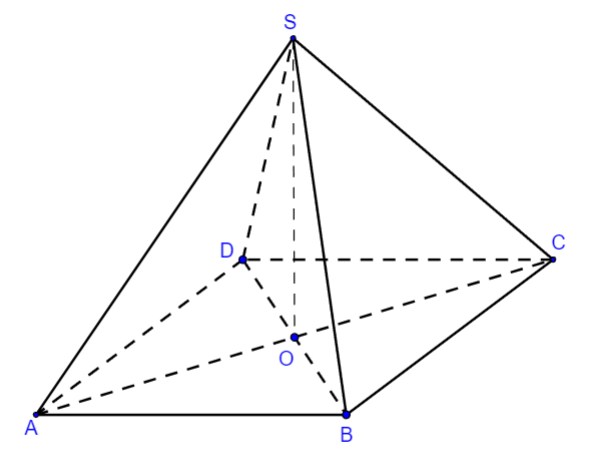
Gọi O là giao điểm của AC và BD khi đó ![]() \(\left\{ \begin{matrix}
CO\bot BD \\
SO\bot BD \\
\end{matrix} \right.\)
\(\left\{ \begin{matrix}
CO\bot BD \\
SO\bot BD \\
\end{matrix} \right.\)
Do đó, góc phẳng nhị diện ![]() \(\lbrack
S,BD,C\rbrack\) bằng góc
\(\lbrack
S,BD,C\rbrack\) bằng góc ![]() \(\widehat{SOC}\)
\(\widehat{SOC}\)
Xét tam giác SAO có: ![]() \(AO = SA =
\frac{a\sqrt{2}}{2}\)
\(AO = SA =
\frac{a\sqrt{2}}{2}\)
![]() \(\widehat{SAO} = 90^{0}\)
\(\widehat{SAO} = 90^{0}\)
Nên tam giác SAO vuông cân tại A
![]() \(\Rightarrow \widehat{SOA} =
45^{0};\widehat{SOC} = 135^{0}\)
\(\Rightarrow \widehat{SOA} =
45^{0};\widehat{SOC} = 135^{0}\)
Vậy số đo góc nhị diện ![]() \(\lbrack
S,BD,C\rbrack\) bằng 1350.
\(\lbrack
S,BD,C\rbrack\) bằng 1350.
Ví dụ 3: Cho hình chóp ![]() \(S.ABC\),
\(S.ABC\), ![]() \(SA\bot(ABC)\),
\(SA\bot(ABC)\), ![]() \(AB = AC = a\),
\(AB = AC = a\), ![]() \(\widehat{BAC} = 120^{0}\),
\(\widehat{BAC} = 120^{0}\), ![]() \(SA = \frac{a\sqrt{3}}{2}\). Tính số đo góc phẳng nhị diện
\(SA = \frac{a\sqrt{3}}{2}\). Tính số đo góc phẳng nhị diện ![]() \(\lbrack
S,BC,A\rbrack\)?
\(\lbrack
S,BC,A\rbrack\)?
Hướng dẫn giải
Hình vẽ minh họa
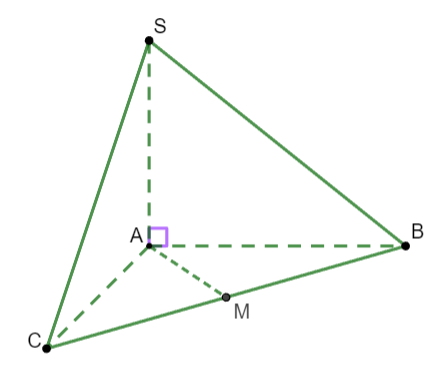
Gọi M là trung điểm của BC
Ta có: ![]() \(AB = AC \Rightarrow AM\bot
BC\)
\(AB = AC \Rightarrow AM\bot
BC\)
Mặt khác SB = SC (do ![]() \(\Delta SAC = \Delta SAB\)) nên tam giác SBC cân tại S
\(\Delta SAC = \Delta SAB\)) nên tam giác SBC cân tại S
![]() \(\Rightarrow SM\bot BC\)
\(\Rightarrow SM\bot BC\)
![]() \(\Rightarrow \widehat{SMA}\) là góc phẳng nhị diện của
\(\Rightarrow \widehat{SMA}\) là góc phẳng nhị diện của ![]() \(\lbrack
S,BC,A\rbrack\).
\(\lbrack
S,BC,A\rbrack\).
Ta có: ![]() \(\widehat{MAB} =
\frac{\widehat{BAC}}{2} = 60^{0}\)
\(\widehat{MAB} =
\frac{\widehat{BAC}}{2} = 60^{0}\)
![]() \(\Rightarrow AM = AB.cos\widehat{MAB} =
\frac{a}{2}\)
\(\Rightarrow AM = AB.cos\widehat{MAB} =
\frac{a}{2}\)
Trong tam giác ![]() \(SAM\) vuông tại A ta có:
\(SAM\) vuông tại A ta có:
![]() \(\tan\widehat{SAM} = \frac{SA}{MA} =
\frac{a\sqrt{3}}{2}.\frac{2}{a} = \sqrt{3}\)
\(\tan\widehat{SAM} = \frac{SA}{MA} =
\frac{a\sqrt{3}}{2}.\frac{2}{a} = \sqrt{3}\)
![]() \(\Rightarrow \widehat{SAM} =
60^{0}\).
\(\Rightarrow \widehat{SAM} =
60^{0}\).
Ví dụ 4. Cho tứ diện ABCD có BCD là tam giác vuông tại đỉnh B, cạnh ![]() \(CD =
a,BD = \frac{a\sqrt{6}}{3}\),
\(CD =
a,BD = \frac{a\sqrt{6}}{3}\), ![]() \(AB = AC
= AD = \frac{a\sqrt{3}}{2}\). Tính cosin của góc nhị diện [A, BC, D].
\(AB = AC
= AD = \frac{a\sqrt{3}}{2}\). Tính cosin của góc nhị diện [A, BC, D].
Hướng dẫn giải:
Gọi M, H lần lượt là trung điểm của BC, CD.
Do ![]() \(\Delta BCD\) vuông tại B nên
\(\Delta BCD\) vuông tại B nên ![]() \(BH = CH
= DH\) hay H là tâm đường tròn ngoại tiếp
\(BH = CH
= DH\) hay H là tâm đường tròn ngoại tiếp ![]() \(\Delta BCD\).
\(\Delta BCD\).
Mà AB = AC = AD nên AH là đường cao kẻ từ A xuống (BCD) hay ![]() \(AH\bot(BCD)\).
\(AH\bot(BCD)\).
![]() \(\Rightarrow AH\bot BC.\) (1)
\(\Rightarrow AH\bot BC.\) (1)
M, H là trung điểm của BC, CD nên MH là đường trung bình của ![]() \(\Delta BCD\)
\(\Delta BCD\)
 \(\Rightarrow \left\{ \begin{matrix}MH = \dfrac{1}{2}BD = \dfrac{a\sqrt{6}}{6}. \\MH//BD \\\end{matrix} ight.\)
\(\Rightarrow \left\{ \begin{matrix}MH = \dfrac{1}{2}BD = \dfrac{a\sqrt{6}}{6}. \\MH//BD \\\end{matrix} ight.\)
Mà ![]() \(MD\bot BC\) nên
\(MD\bot BC\) nên ![]() \(MH\bot BC\). (2)
\(MH\bot BC\). (2)
Từ (1), (2) suy ra: ![]() \(BC\bot(AMH)\).
\(BC\bot(AMH)\).
Suy ra: ![]() \(\left\{ \begin{matrix}
BC\bot AM \\
BC\bot MH \\
\end{matrix} \Rightarrow \lbrack A,BC,Dbrack = \widehat{AMH} ight.\).
\(\left\{ \begin{matrix}
BC\bot AM \\
BC\bot MH \\
\end{matrix} \Rightarrow \lbrack A,BC,Dbrack = \widehat{AMH} ight.\).
Lại có:  \(AH = \sqrt{AC^{2} - CH^{2}} =
\sqrt{\left( \frac{a\sqrt{3}}{2} ight)^{2} - \left( \frac{a}{2}
ight)^{2}} = \frac{a\sqrt{2}}{2}\).
\(AH = \sqrt{AC^{2} - CH^{2}} =
\sqrt{\left( \frac{a\sqrt{3}}{2} ight)^{2} - \left( \frac{a}{2}
ight)^{2}} = \frac{a\sqrt{2}}{2}\).
![]() \(\Rightarrow \tan\widehat{AMH} =
\frac{AH}{MH} = \sqrt{3}\)
\(\Rightarrow \tan\widehat{AMH} =
\frac{AH}{MH} = \sqrt{3}\)![]() \(\Rightarrow \widehat{AMH} = \frac{\pi}{3}\)
\(\Rightarrow \widehat{AMH} = \frac{\pi}{3}\)![]() \(\Rightarrow \cos\widehat{AMH} = \frac{1}{2}.\)
\(\Rightarrow \cos\widehat{AMH} = \frac{1}{2}.\)
5. Bài tập tự rèn luyện có hướng dẫn đáp án cụ thể
Bài tập 1. Cho hình chóp tứ giác đều ![]() \(S.ABCD\),
\(S.ABCD\), ![]() \(O\)là giao điểm của
\(O\)là giao điểm của ![]() \(AC\) và
\(AC\) và ![]() \(BD\),
\(BD\), ![]() \(M\) là trung điểm
\(M\) là trung điểm ![]() \(AD\). Góc nào sau đây là góc phẳng nhị diện của góc nhị diện
\(AD\). Góc nào sau đây là góc phẳng nhị diện của góc nhị diện ![]() \(\lbrack
B,AD,S\rbrack\)?
\(\lbrack
B,AD,S\rbrack\)?
A. ![]() \(\widehat{SAB}\). B.
\(\widehat{SAB}\). B. ![]() \(\widehat{SDB}\). C.
\(\widehat{SDB}\). C. ![]() \(\widehat{SMO}\). D.
\(\widehat{SMO}\). D. ![]() \(\widehat{SMB}\).
\(\widehat{SMB}\).
Bài tập 2. Cho hình chóp ![]() \(S.ABCD\) có
\(S.ABCD\) có ![]() \(SA\bot(ABCD),ABCD\) là hình thoi cạnh
\(SA\bot(ABCD),ABCD\) là hình thoi cạnh ![]() \(a,AC = a\),
\(a,AC = a\), ![]() \(SA = \frac{a}{2}\). Gọi
\(SA = \frac{a}{2}\). Gọi ![]() \(H\) là hình chiếu của
\(H\) là hình chiếu của ![]() \(S\) trên cạnh
\(S\) trên cạnh ![]() \(CD\). Xét tính đúng sai của các khẳng định dưới đây?
\(CD\). Xét tính đúng sai của các khẳng định dưới đây?
a) ![]() \(AH\bot CD\).
\(AH\bot CD\).
b) ![]() \(AH = \frac{a\sqrt{3}}{2}\).
\(AH = \frac{a\sqrt{3}}{2}\).
c) Góc ![]() \(SDC\) là góc phẳng nhị diện của góc nhị diện
\(SDC\) là góc phẳng nhị diện của góc nhị diện ![]() \(\lbrack
S,CD,A\rbrack\).
\(\lbrack
S,CD,A\rbrack\).
d) Số đo của góc nhị diện ![]() \(\lbrack
S,CD,A\rbrack\) bằng
\(\lbrack
S,CD,A\rbrack\) bằng ![]() \(30^{\circ}\).
\(30^{\circ}\).
Bài tập 3. Cho hình lâp phương  \(ABCD.A'B'C'D'\). Xét tính đúng sai của các khẳng định dưới đây?
\(ABCD.A'B'C'D'\). Xét tính đúng sai của các khẳng định dưới đây?
a) Góc giữa hai đường thẳng ![]() \(AB\) và
\(AB\) và  \(A'C'\) bằng
\(A'C'\) bằng ![]() \(45^{\circ}\).
\(45^{\circ}\).
b) Gọi ![]() \(\alpha\) là góc giữa đường thẳng
\(\alpha\) là góc giữa đường thẳng  \(A'C\) và mặt phẳng
\(A'C\) và mặt phẳng  \(\left( A'B'C'D \right.\)). Giá trị
\(\left( A'B'C'D \right.\)). Giá trị ![]() \(\tan\alpha\) bằng
\(\tan\alpha\) bằng ![]() \(\sqrt{2}\).
\(\sqrt{2}\).
c) Gọi ![]() \(\beta\) là số đo của góc nhị diện
\(\beta\) là số đo của góc nhị diện  \(\lbrack
B,A'C',B'\rbrack\). Giá trị
\(\lbrack
B,A'C',B'\rbrack\). Giá trị ![]() \(\tan\beta\) bằng
\(\tan\beta\) bằng ![]() \(\frac{\sqrt{2}}{2}\).
\(\frac{\sqrt{2}}{2}\).
d) Số đo của góc nhị diện  \(\lbrack
B',A'C,D'\rbrack\) bằng
\(\lbrack
B',A'C,D'\rbrack\) bằng ![]() \(120^{\circ}\).
\(120^{\circ}\).
Bài tập 4. Cho hình chóp ![]() \(S.ABCD\) có đáy là hình vuông cạnh
\(S.ABCD\) có đáy là hình vuông cạnh ![]() \(a\),
\(a\), ![]() \(SA\bot(ABCD)\) và số đo của góc nhị diện
\(SA\bot(ABCD)\) và số đo của góc nhị diện ![]() \(\lbrack S,BC,A\rbrack\) bằng
\(\lbrack S,BC,A\rbrack\) bằng ![]() \(60^{\circ}\). Khoảng cách giữa hai đường thẳng
\(60^{\circ}\). Khoảng cách giữa hai đường thẳng ![]() \(SC\) và
\(SC\) và ![]() \(BD\) bằng
\(BD\) bằng ![]() \(\frac{a\sqrt{30}}{n}\). Tìm giá trị của
\(\frac{a\sqrt{30}}{n}\). Tìm giá trị của ![]() \(n\).
\(n\).
Đáp án chi tiết bài tập vận dụng
Bài tập 1.
Hình vẽ minh họa:
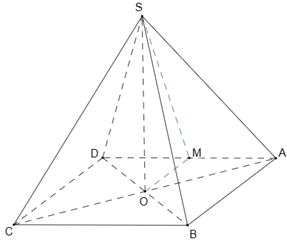
Chọn C
Ta có:
![]() \(O,M\)lần lượt là trung điểm của
\(O,M\)lần lượt là trung điểm của![]() \(BD,AD\)nên song song với
\(BD,AD\)nên song song với ![]() \(AB\)mà
\(AB\)mà ![]() \(AB\bot
AD \Rightarrow OM\bot ADS.ABCD\) đều
\(AB\bot
AD \Rightarrow OM\bot ADS.ABCD\) đều ![]() \(\Rightarrow SAD\) cân tại
\(\Rightarrow SAD\) cân tại ![]() \(S \Rightarrow SM\bot AD\)
\(S \Rightarrow SM\bot AD\)
Có: ![]() \(\left\{ \begin{matrix}
OM\bot AD \\
SM\bot AD
\end{matrix} \right.\ \Rightarrow \lbrack B,AD,S\rbrack =
\widehat{SMO}\).
\(\left\{ \begin{matrix}
OM\bot AD \\
SM\bot AD
\end{matrix} \right.\ \Rightarrow \lbrack B,AD,S\rbrack =
\widehat{SMO}\).
📥 Để xem trọn vẹn nội dung, ví dụ minh họa, bạn vui lòng tải tài liệu tham khảo tại đây.
----------------------------------
Như vậy, việc tính góc nhị diện không chỉ đơn giản là áp dụng công thức, mà còn là quá trình hiểu rõ về mối quan hệ giữa các mặt phẳng và đường thẳng trong không gian 3D. Hướng dẫn tính góc nhị diện nhanh, chính xác mà chúng tôi cung cấp sẽ giúp bạn dễ dàng nắm vững các phương pháp từ cơ bản đến nâng cao, áp dụng vào các bài toán hình học trong thực tế. Bằng cách thực hành thường xuyên, bạn sẽ cải thiện khả năng giải quyết các bài toán phức tạp liên quan đến góc nhị diện.
Nếu bạn cảm thấy cần thêm ví dụ cụ thể, hoặc muốn khám phá các ứng dụng thực tế của tính góc nhị diện trong các ngành học như hình học không gian, cơ học hay kỹ thuật, đừng ngần ngại tham khảo thêm các bài viết chi tiết trên website của chúng tôi. Chúng tôi luôn cập nhật những kiến thức mới và các mẹo giải bài toán hình học hiệu quả, giúp bạn nâng cao trình độ một cách nhanh chóng.
Hy vọng rằng bài viết này đã giúp bạn có cái nhìn rõ ràng và chi tiết hơn về cách tính góc nhị diện. Nếu có bất kỳ câu hỏi nào, hoặc bạn muốn chia sẻ những kinh nghiệm cá nhân trong việc tính toán góc nhị diện, hãy để lại ý kiến của bạn trong phần bình luận dưới bài viết. Chúng tôi sẽ trả lời nhanh chóng và chi tiết để bạn không còn gặp khó khăn trong việc tính toán này.











