Công thức tính tứ phân vị
Công thức tứ phân vị
Tứ phân vị là một khái niệm quan trọng trong thống kê thành phần dữ liệu tập các phần sử dụng để phân bố cục. Tài liệu dưới đây là một khái niệm quan trọng trong thống kê, giúp chia dữ liệu thành bốn thành phần để phân tích bố cục. Bài viết dưới đây sẽ giới thiệu chi tiết công thức tứ phân vị, cách tính và ý nghĩa của từng phần trong thực tế.
A. Tứ phân vị là gì?
Tứ phân vị (tiếng Anh: quartiles) là các giá trị chia một tập hợp số liệu thành bốn phần bằng nhau theo thứ tự tăng dần, mỗi phần chiếm 25% số liệu. Chúng giúp mô tả sự phân bố và mức độ phân tán của dữ liệu.
Có 3 tứ phân vị chính:
Tứ phân vị thứ nhất (Q1) – Còn gọi là phân vị thứ 25: Là giá trị mà 25% số liệu nhỏ hơn hoặc bằng nó.
Tứ phân vị thứ hai (Q2) – Chính là trung vị (median): Là giá trị chia dữ liệu thành hai nửa bằng nhau (50% nhỏ hơn, 50% lớn hơn).
Tứ phân vị thứ ba (Q3) – Phân vị thứ 75: Là giá trị mà 75% số liệu nhỏ hơn hoặc bằng nó.
B. Cách tính tứ phân vị của mẫu dữ liệu ghép nhóm
Cho mẫu số liệu ghép nhóm:
|
Nhóm |
 \(\left\lbrack a_{1};a_{2}
\right)\) |
… |
\(\left\lbrack a_{i};a_{i + 1}
\right)\) |
… |
\(\left\lbrack a_{k};a_{k + 1}
\right)\) |
|
Tần số |
\(m_{1}\) |
… |
\(m_{i}\) |
… |
\(m_{k}\) |
Công thức Tứ phân vị thứ nhất
Để tìm tứ phân vị thứ nhất \(Q_{1}\) của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa \(Q_{1}\), giả sử đó là nhóm thứ p: \(\left\lbrack a_{p};a_{p + 1} \right)\). Khi đó:
\(Q_{1} = a_{p} + \dfrac{\dfrac{n}{4} -
\left( m_{1} + ... + m_{p - 1} \right)}{m_{p}}.\left( a_{p + 1} - a_{p}
\right)\)
Trong đó n là cỡ mẫu, \(m_{p}\) là tần số nhóm p, với p = 1 ta quy ước \(m_{1} +
... + m_{p - 1} = 0\).
Công thức tính tứ phân vị thứ ba
Để tìm tứ phân vị thứ ba \(Q_{3}\) của mẫu số liệu ghép nhóm, trước hết ta xác định nhóm chứa \(Q_{3}\), giả sử đó là nhóm thứ p: \(\left\lbrack a_{p};a_{p + 1} \right)\). Khi đó:
\(Q_{3} = a_{p} + \dfrac{\dfrac{3n}{4} -
\left( m_{1} + ... + m_{p - 1} \right)}{m_{p}}.\left( a_{p + 1} - a_{p}
\right)\)
Trong đó n là cỡ mẫu, \(m_{p}\) là tần số nhóm p, với p = 1 ta quy ước \(m_{1} +
... + m_{p - 1} = 0\).
Tứ phân vị thứ hai \(Q_{2}\) chính là trung vị \(M_{e}\).
Công thức tính khoảng tứ phân vị
Khoảng tứ phân vị, kí hiệu là \(\Delta_{Q}\) là hiệu số giữa tứ phân vị thứ ba và tứ phân vị thứ nhất, tức là: \(\Delta_{Q} = Q_{3} - Q_{1}\)
C. Bài tập tính tứ phân vị
Ví dụ. Cho bảng thống kê chiều cao (đơn vị: cm) của học sinh lớp 12A và lớp 12B như sau:
|
Chiều cao |
[155; 160) |
[160; 165) |
[165; 170) |
[170; 175) |
[175; 180) |
[180; 185) |
|
12A |
2 |
7 |
12 |
3 |
0 |
1 |
|
12B |
5 |
9 |
8 |
2 |
1 |
0 |
Em có nhận xét gì về độ phân tán của hai lớp 12A và 12B?
Hướng dẫn giải
Ta có:
|
Chiều cao |
[155; 160) |
[160; 165) |
[165; 170) |
[170; 175) |
[175; 180) |
[180; 185) |
|
12A |
2 |
7 |
12 |
3 |
0 |
1 |
|
Tần số tích lũy |
2 |
9 |
21 |
24 |
24 |
25 |
Cỡ mẫu \(N = 25\). Gọi \(x_{1};x_{2};...;x_{25}\) là mẫu số liệu gốc
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( x_{6} + x_{7} \right)\) thuộc nhóm [160; 165)
\(Q_{1} = 160 + \dfrac{\dfrac{25}{4} -2}{7}(165 - 160) = \dfrac{4565}{28}\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( x_{19} + x_{20} \right)\) thuộc nhóm [165; 170)
\(Q_{3} = 165 + \dfrac{3.\dfrac{25}{4} -9}{12}(170 - 165) = \dfrac{2705}{16}\)
Do đó khoảng tứ phân vị \(\Delta_{Q} =
Q_{3} - Q_{1} = \frac{675}{112} \approx 6,03\)
|
Chiều cao |
[155; 160) |
[160; 165) |
[165; 170) |
[170; 175) |
[175; 180) |
[180; 185) |
|
12B |
5 |
9 |
8 |
2 |
1 |
0 |
|
Tần số tích lũy |
5 |
14 |
22 |
24 |
25 |
25 |
Cỡ mẫu \(N = 25\). Gọi \(x_{1};x_{2};...;x_{25}\) là mẫu số liệu gốc
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( x_{6} + x_{7} \right)\) thuộc nhóm [160; 165)
\(Q_{1} = 160 + \dfrac{\dfrac{25}{4} -5}{9}(165 - 160) = \dfrac{5785}{36}\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}\left( x_{19} + x_{20} \right)\) thuộc nhóm [165; 170)
\(Q_{3} = 165 + \dfrac{3.\dfrac{25}{4} -14}{8}(170 - 165) = \dfrac{5375}{32}\)
Do đó khoảng tứ phân vị \(\Delta_{Q} =
Q_{3} - Q_{1} = 7,27\)
Vậy nửa giữa mẫu số liệu chiều cao của học sinh lớp 12A có độ phân tán nhỏ hơn lớp 12B.
Ví dụ: Cho biểu đồ thống kê thời gian tập thể dục buổi sáng của hai người A và B
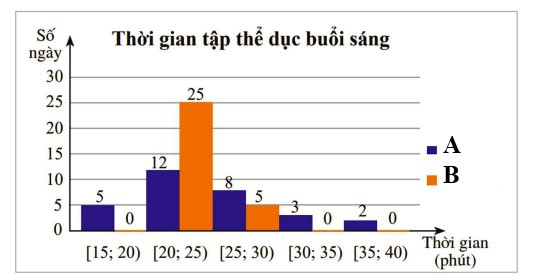
Gọi khoảng tứ phân vị của mẫu số liệu về thời gian tập thể dục của A và B lần lượt là \(\Delta_{Q_{A}};\Delta_{Q_{B}}\). So sánh \(\Delta_{Q_{A}};\Delta_{Q_{B}}\)?
Hướng dẫn giải
Ta có:
|
Đối tượng |
[15; 20) |
[20; 25) |
[25; 30) |
[30; 35) |
[35; 40) |
|
A |
5 |
12 |
8 |
3 |
2 |
|
Tần số tích lũy |
5 |
17 |
25 |
28 |
30 |
Cỡ mẫu \(N = 30 \Rightarrow \frac{N}{4} =
7,5\)
=> Nhóm chứa \(Q_{1}\) là: [20; 25)
Khi đó ta tìm được các giá trị:
\(\Rightarrow l = 20;m = 5,f = 12;c = 25 -
20 = 5\)
\(\Rightarrow Q_{1} = l +
\dfrac{\dfrac{N}{4} - m}{f}.c\)\(= 20 + \dfrac{7,5 - 5}{12}.5 =
\dfrac{505}{24}\)
Cỡ mẫu \(\frac{3N}{4} = 22,5\)
=> Nhóm chứa \(Q_{3}\) là [25; 30)
Khi đó ta tìm được các giá trị:
\(\Rightarrow l = 25;m = 17,f = 8;c =
5\)
\(\Rightarrow Q_{3} = l +
\dfrac{\dfrac{3N}{4} - m}{f}.c\)\(= 25 + \dfrac{22,5 - 17}{8}.5 =\dfrac{455}{16}\).
Vậy khoảng tứ phân vị của mẫu số liệu về thời gian tập thể dục của A là:
\(\Delta_{Q_{A}} = Q_{3} - Q_{1} =
\frac{355}{48} \approx 7,4\).
|
Đối tượng |
[15; 20) |
[20; 25) |
[25; 30) |
[30; 35) |
[35; 40) |
|
B |
0 |
25 |
5 |
0 |
0 |
|
Tần số tích lũy |
0 |
25 |
30 |
0 |
0 |
Cỡ mẫu \(N = 30 \Rightarrow \frac{N}{4} =
7,5\)
=> Nhóm chứa \(Q_{1}\) là: [20; 25)
Khi đó ta tìm được các giá trị:
\(\Rightarrow l = 20;m = 0,f = 25;c = 25 -
20 = 5\)
\(\Rightarrow Q_{1} = l +
\dfrac{\dfrac{N}{4} - m}{f}.c\)\(= 20 + \dfrac{7,5 - 0}{25}.5 =
\dfrac{43}{2}\)
Cỡ mẫu \(\frac{3N}{4} = 22,5\)
=> Nhóm chứa \(Q_{1}\) là: [20; 25)
Khi đó ta tìm được các giá trị:
\(\Rightarrow l = 20;m = 0,f = 25;c = 25 -
20 = 5\)
\(\Rightarrow Q_{3} = l +
\dfrac{\dfrac{3N}{4} - m}{f}.c\)\(= 20 + \dfrac{22,5 - 0}{25}.5 =
\dfrac{49}{2}\).
Vậy khoảng tứ phân vị của mẫu số liệu về thời gian tập thể dục của B là:
\(\Delta_{Q_{B}} = Q_{3} - Q_{1} =
3\).
Vậy kết luận đúng là: \(\Delta_{Q_{A}} >
\Delta_{Q_{B}}\).
Ví dụ. Thời gian truy cập internet mỗi buổi trưa của một số học sinh được cho trong bảng sau:
|
Thời gian (phút) |
\(\lbrack
9,5;12,5)\) |
\(\lbrack
12,5;15,5)\) |
\(\lbrack
15,5;18,5)\) |
\(\lbrack
18,5;21,5)\) |
\(\lbrack
21,5;24,5)\) |
|
Số học sinh |
3 |
12 |
15 |
24 |
2 |
Tìm tứ phân vị thứ nhất và tứ phân vị thứ ba của dãy số liệu trên. (Kết quả làm tròn đến hàng phần chục)
Hướng dẫn giải
Cỡ mẫu là: \(n = 3 + 12 + 15 + 24 + 2 =
56\).
Gọi \(x_{1};...;x_{56}\) là thời gian truy cập internet của 56 học sinh và giả sữ dãy này đã được sắp xếp theo thứ tự tăng dần.
Khi đó, tứ phân vị thứ nhất là \(Q_{1} =
\frac{x_{14} + x_{15}}{2}\).
Do \(x_{14},\ x_{15} \in \lbrack 12,5;\
15,5)\) nên \(Q_{1} = 12,5 +
\frac{\frac{56}{4} - 3}{12}.3 \approx 15,3\)
Tứ phân vị thứ ba là \(Q_{3} = \frac{x_{42}
+ x_{43}}{2}\).
Do \(x_{14},\ x_{15} \in \lbrack 18,5;\
21,5)\) nên \(Q_{3} = 18,5 +
\frac{\frac{3.56}{4} - 30}{24}.3 = 20\)
Vậy tứ phân vị thứ nhất của mẫu số liệu đã cho là 15,3
Tứ phân vị thứ nhất của mẫu số liệu đã cho là 20.
------------------------------------------------------------------------
Việc áp dụng công thức tính tứ phân vị không chỉ giúp bạn phân tích và hiểu rõ hơn về đặc điểm phân bố của dữ liệu, mà còn là nền tảng quan trọng trong nhiều bài toán thống kê và phân tích dữ liệu. Thông qua mẫu số liệu ghép nhóm, bạn có thể dễ dàng xác định các điểm phân vị quan trọng như Q1, Q2, Q3, giúp cải thiện khả năng dự báo và ra quyết định chính xác hơn. Tuy nhiên, để nắm vững và áp dụng thành thạo công thức này, bạn cần kiên nhẫn và thực hành nhiều lần. Đặc biệt, việc hiểu sâu về các phương pháp ghép nhóm dữ liệu sẽ giúp bạn tối ưu hóa quy trình tính toán và nâng cao hiệu quả phân tích.
Nếu bạn đang tìm kiếm thêm các phương pháp tính toán thống kê nâng cao hoặc cách áp dụng các công thức thống kê trong thực tế, đừng ngần ngại tham khảo các bài viết khác trên website của chúng tôi. Chúng tôi luôn cập nhật các kiến thức mới nhất về thống kê, phân tích dữ liệu, và công cụ phần mềm hỗ trợ giúp bạn tiến xa hơn trong nghiên cứu và công việc của mình. Hy vọng bài viết đã giúp bạn hiểu rõ hơn về công thức tính tứ phân vị và mẫu số liệu ghép nhóm. Nếu có bất kỳ thắc mắc nào hoặc cần thêm ví dụ cụ thể, hãy để lại câu hỏi trong phần bình luận phía dưới. Chúng tôi sẽ cố gắng trả lời mọi câu hỏi của bạn một cách chi tiết và dễ hiểu nhất.
